Содержание
- 2. Логическое мышление
- 3. Логическое мышление – это мыслительный процесс, при котором человек использует логические понятия и конструкции, которому свойственна
- 4. Развитие логического мышления при изучении математики состоит в формировании у учащихся характерных для этого предмета приемов
- 5. Проблема развития логического мышления очень актуальна в ходе реализации ФГОС НОО. В стандарте обозначено, что в
- 6. Очевидно, что одной лишь работы с готовыми алгоритмами арифметических действий, эпизодического решения логических задач, что обычно
- 7. Логическое мышление в начальной школе Уже в начальной школе дети должны овладеть элементами логических действий (сравнения,
- 8. В работах В.В. Занков, В.В. Давыдов, Л.М. Фридман доказывается, что в результате правильно организованного обучения младшие
- 9. Большинство исследователей считают, что развивать логическое мышление в процессе обучения это значит: Развивать у учащихся умение
- 10. Основная работа для развития логического мышления должна вестись с задачей. Ведь в любой задаче заложены большие
- 11. Основная работа для развития логического мышления должна вестись с задачей. Ведь в любой задаче заложены большие
- 12. Наибольший эффект при этом может быть достигнут в результате применения разных форм работы над задачей. Формы
- 13. 1. Работа над решенной задачей Многие ученики только после повторного анализа осознают план решения задачи. Это
- 14. 2. Решение задач разными способами Мало уделяется внимания решению задач разными способами в основном из-за недостатка
- 15. 3. Представление ситуации, описанной в задаче. Учитель обращает внимание детей на детали задачи, которые нужно обязательно
- 16. 4. Самостоятельное составление задач учениками.
- 17. Составить задачу: 1. используя слова: больше на, столько,, меньше в, на столько больше, на столько меньше;
- 18. Систематическое использование на уроках математики и внеурочных занятий специальных задач и заданий, направленных на развитие логического
- 19. Нестандартные задачи требуют повышенного внимания к анализу условия и построения цепочки взаимосвязанных логических рассуждений. Приведу примеры
- 20. Пример задачи Батон разрезали на 3 части. Сколько сделали разрезов?
- 21. С использование таких задач расширяет математический кругозор младших школьников, способствует математическому развитию и повышает качество математической
- 22. Алгоритмическое мышление
- 23. Алгоритмическое мышление – это система мыслительных действий и приемов, направленных на решение теоретических и практических задач,
- 24. Навыки алгоритмического мышления способствуют также формированию особого стиля культуры человека, составляющими которого являются: Целеустремленность и сосредоточенность
- 25. Формирование алгоритмического мышления-важная составляющая часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить
- 26. Программа предусматривает: Формирование умений действовать по предложенному алгоритму Самостоятельно составлять план действий и следовать ему при
- 27. Задача учителя – больше использовать эти возможности при обучении детей математике. И дополнительные упражнения в учебнике,
- 28. Алгоритмическое умение
- 29. Умение последовательно чётко и непротиворечиво излагать свои мысли тесно связано с умением представлять сложные действия в
- 30. Оно находит своё выражение в том, что человек, видя конечную цель, может составить алгоритмическое предписание или
- 31. Что же такое алгоритм? Под алгоритмом мы будем понимать точное описание некоторой последовательности действий.
- 32. Алгоритм – это жёсткое предписание о выполнении в определённой последовательности элементарных операций для решения познавательных задач.
- 33. Взаимосвязь логического и алгоритмического мышления Развитие алгоритмического мышления учеников тесно связано с развитием логического мышления, так
- 34. Развитие умения использовать и составлять алгоритм – это основа компьютерной грамотности, а, следовательно, является необходимым умением
- 35. Воспитание алгоритмического мышления начинается в первом классе, где учеников знакомят с простейшими алгоритмами. Алгоритм заваривания чая
- 36. Эти алгоритмы могут быть представлены как в виде последовательности картинок, так и сформулированы в виде предложений.
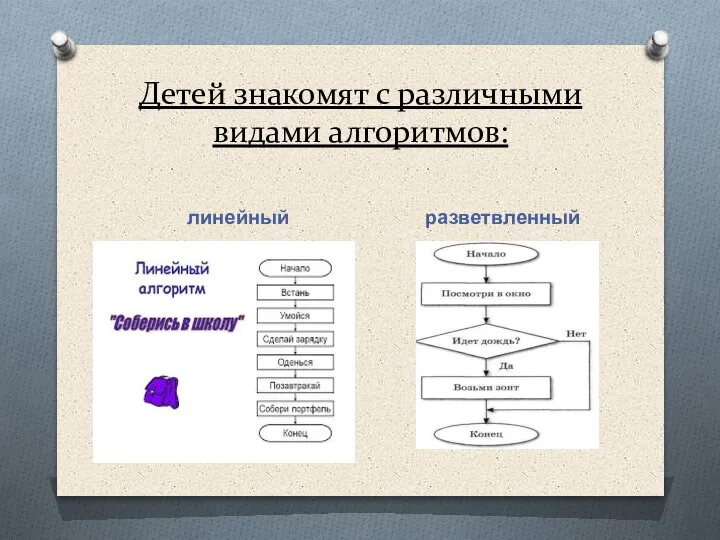
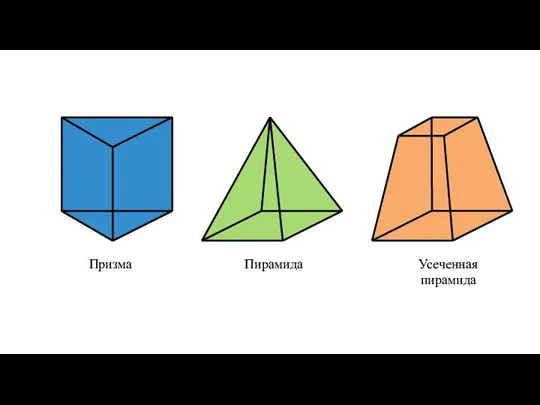
- 37. Детей знакомят с различными видами алгоритмов: линейный разветвленный
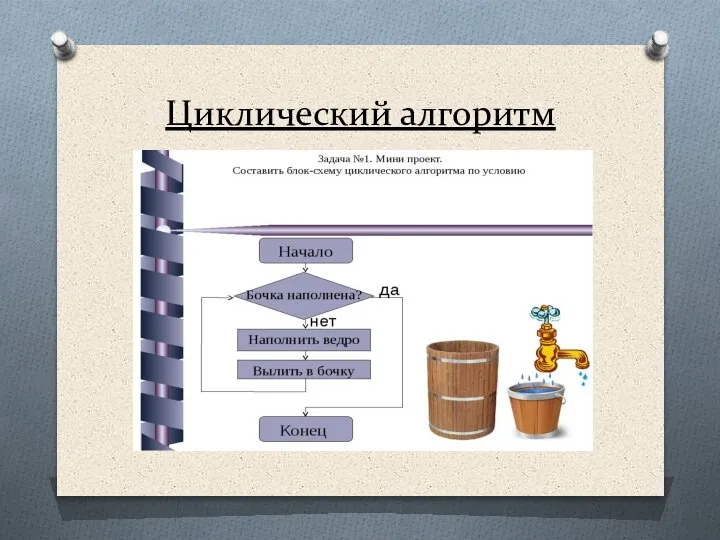
- 38. Циклический алгоритм
- 39. Игра «РОБОТ» Одним из распространённых упражнений в 1 классе для развития алгоритмического мышления является игра «Робот».
- 40. Команда «Построй чертеж» Можно предложить такие задания: по чертежу составь алгоритм его построения; найди ошибки в
- 41. Позднее при изучении математических понятий алгоритм включается как в процесс изучения математических понятий, так и в
- 42. Основной формой предъявления ученикам алгоритмических предписаний являются блок – схемы, граф – схемы, таблицы. Блок –
- 43. Таблица – содержит несколько строк. Указан способ её заполнения. Заполнение таблицы готовит к восприятию идеи описания
- 44. Для формирования у учащихся умения выявлять способ действия полезны комбинаторные задания. Их особенность в том, что
- 45. Для решения этой комбинаторной задачи можно воспользоваться построением «дерева рассуждений». Выписывается сначала одна цифра, с которой
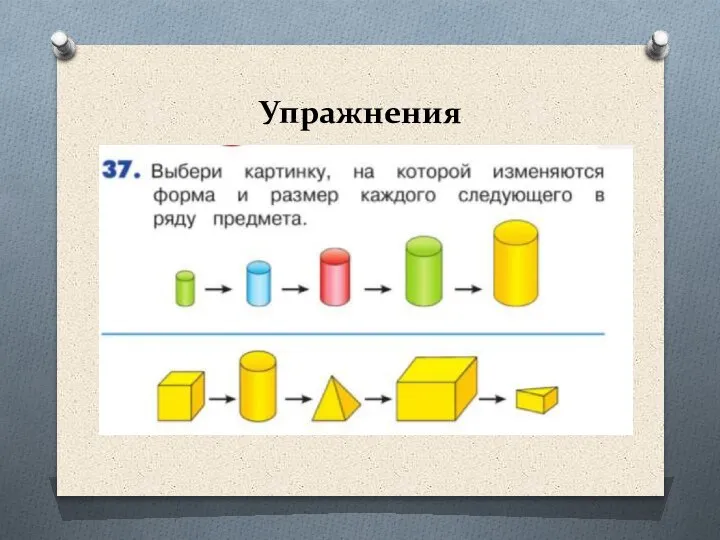
- 46. Примеры упражнений, которые может использовать учитель на уроках математики с целью формирования алгоритмического мышления младших школьников.
- 47. Упражнения Установи последовательность действий на данной картинке.
- 48. Упражнения Составьте и нарисуйте правила поведения в компьютерном классе.
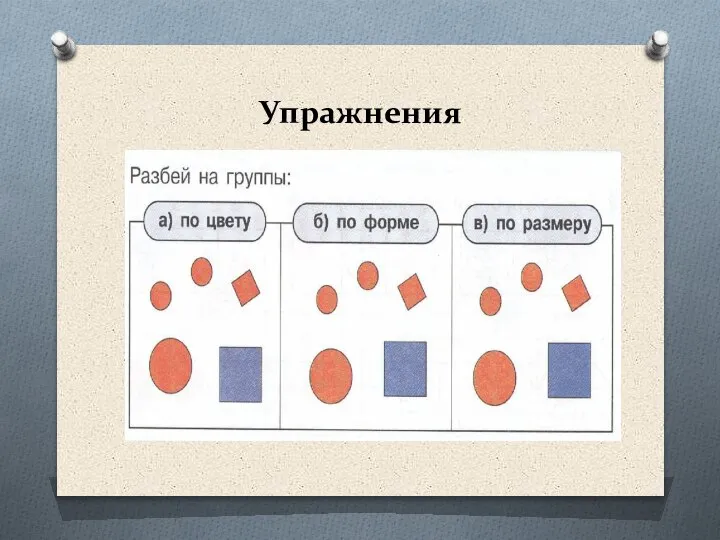
- 49. Упражнения
- 50. Упражнения
- 51. Упражнения
- 52. Упражнения
- 53. Упражнения
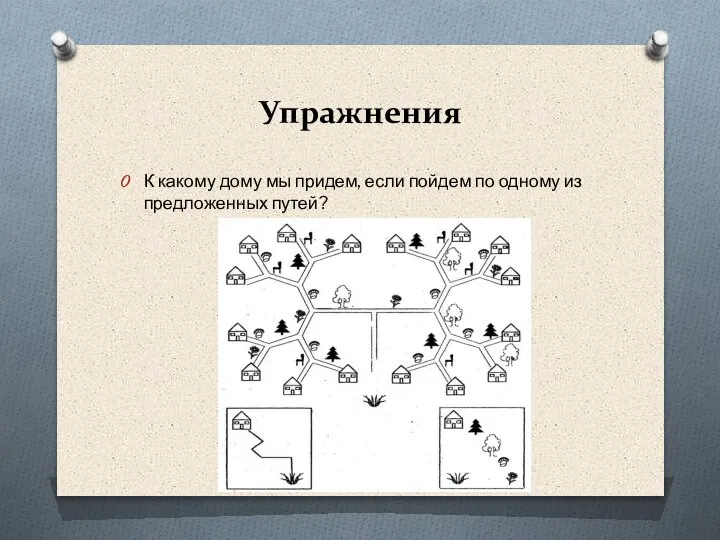
- 54. Упражнения К какому дому мы придем, если пойдем по одному из предложенных путей?
- 55. Упражнения
- 56. Упражнения
- 57. Анализ учебников
- 58. Возможность использования алгоритмов при изучении основных математических понятий по темам: а) нумерация; б) арифметические действия; в)
- 59. Нумерация М1Ич1с34
- 60. Нумерация М1Пч1с28
- 61. Нумерация М1Ач1с27 1-начинаем писать меньшую палочку немного выше середины клетки 2-ведем ее к вершине верхнего правого
- 62. Алгоритм сравнения чисел между собой М1мч1с46
- 63. Алгоритм сравнения чисел между собой М1Ич1с76
- 64. Алгоритм сравнения чисел между собой М1Ач1с40
- 65. Алгоритм сравнения трехзначных чисел М2Пч1с46
- 66. Алгоритм сравнения трехзначных чисел М4Мч1с27
- 67. Алгоритм прочтения многозначных чисел М4Мч1с24
- 68. Алгоритм записи многозначного числа М4Мч1с25
- 69. Программа М.И. Моро Б) Арифметические действия Алгоритм сложения двузначных чисел в столбик М2Мч2с4
- 70. Арифметические действия Алгоритм вычитания двузначных чисел в столбик М2Мч2с5
- 71. Арифметические действия М4М ч.1 стр.12
- 72. Программа Петерсон Л.Г. А) Нумерация М3Пч1с60
- 73. Алгоритм записи трехзначного числа М2Пч1с40
- 74. Программа Л.Г. Петерсон Б) Арифметические действия М2Пч1с12
- 75. Арифметические действия Вычитание двузначных чисел в столбик М2Пч1с18
- 76. Арифметические действия Алгоритм деления двузначного числа на однозначное М2Пч3с61
- 77. Арифметические действия Алгоритм деления двузначного числа на однозначное М2Пч3с68
- 78. Арифметические действия Алгоритм деления двузначного числа на двузначное М2Пч3с72
- 79. Арифметические действия Алгоритм деления с остатком М2Пч2с79
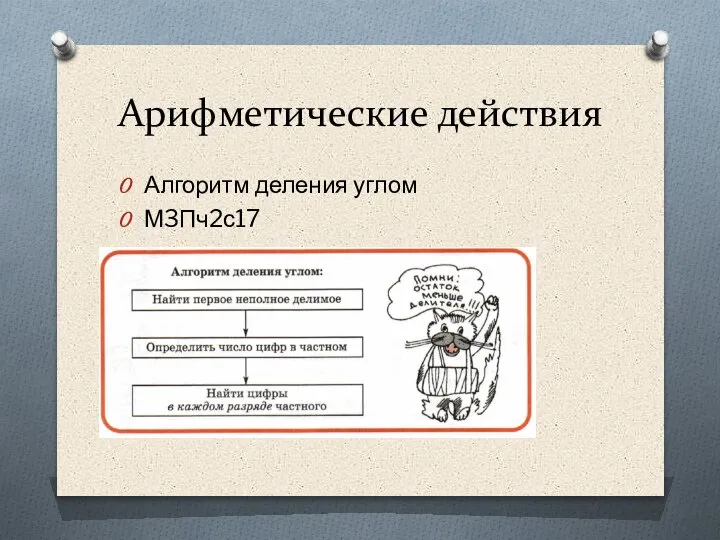
- 80. Арифметические действия Алгоритм деления углом М3Пч2с17
- 81. Арифметические действия М2Пч2с107
- 82. Программа И.И. Аргинской Б) Арифметические действия Алгоритм деления трехзначного числа на однозначное М3Ач2с20
- 83. Арифметические действия М3А ч.1 стр.60
- 84. Арифметические действия М3А ч.1 стр.62
- 85. Арифметические действия М3А ч.1 стр.66
- 86. Арифметические действия М4А ч.1 стр.60
- 87. Программа Н.Б. Истоминой Б) Арифметические действия М4И ч.1 стр.20
- 88. Арифметические действия М4И ч.1 стр.21
- 89. Арифметические действия М4И ч.1 стр.41
- 90. Арифметические действия М4И ч.1 стр.54
- 91. Программа Л.Г. Петерсон В) Задачи М2Пч1с76
- 92. Программа М.И. Моро В) Задачи М1М, ч.2, с.62
- 93. Задачи М2М ч.2 стр.48
- 94. Задачи М2М ч.2 стр.58
- 95. Задачи М2М, ч.2, с.60
- 96. Задачи М3М ч.1 стр.41
- 97. Программа И.И. Аргинской В) Задачи М1А ч.2 стр.44
- 98. Программа М.И. Моро Г) Геометрический материал Алгоритм построения прямой, луча, отрезка М1Мч1с40
- 99. Геометрический материал Алгоритм построения окружности М3Мч1с94
- 100. Программа Н.Б. Истоминой Г) Геометрический материал Алгоритм построения отрезка М1Ич1с65
- 101. Геометрические фигуры М2И, ч.1, с.74
- 102. Геометрические фигуры М2И ч.1 стр.84
- 103. Геометрические фигуры М2И ч.2 стр.104
- 104. Программа И.И. Аргинской Г) Геометрический материал Алгоритм построения замкнутой линии М1Ач1с108
- 105. Программа Чекина Г) Геометрические фигуры М1Ч, ч.1, с.46
- 106. Геометрические фигуры М1Ч, ч.1, с.50
- 107. Геометрические фигуры М2Ч, ч.2, с.47
- 108. Геометрические фигуры М2Ч, ч.2, с.49
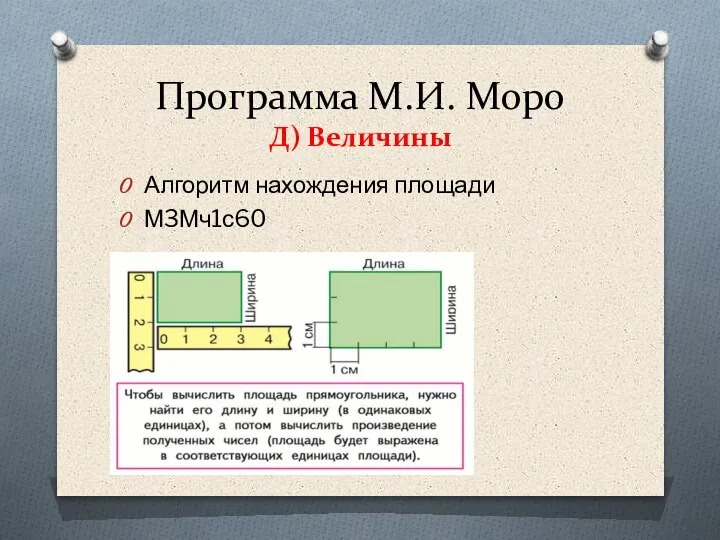
- 109. Программа М.И. Моро Д) Величины Алгоритм нахождения площади М3Мч1с60
- 110. Величины Алгоритм использования палетки М3Мч1с43
- 111. Величины М1М ч.2 с. 60 Ученики учатся сравнивать величины и вводится алгоритм: 1. Переведём крупные единицы
- 112. Величины М3М ч.2 с.70 Ученики учатся выполнять вычисления с величинами по алгоритму: 1. Переводим крупные единицы
- 113. Величины М4М ч.1 с.67 Ученики учатся выполнять вычисления с величинами по алгоритму: 1. Переводим крупные единицы
- 114. Программа Н.Б. Истоминой Д) Величины М1И ч.2 с. 77
- 115. Величины М2И ч.1 с.23
- 116. Программа Л.Г. Петерсон Е) Алгебраический материал Алгоритм решения уравнений М2Пч2с95
- 117. Алгебраический материал М3Пч2с83
- 118. Алгебраический материал М3Пч2с с101
- 119. Программа М.И. Моро Е) Алгебраический материал М3М ч.1 с.24 Алгоритм решения выражения
- 120. Алгебраический материал М2М ч.1 с.80
- 121. Программа Н.Б. Истоминой Е) Алгебраический материал М4И ч.2 с.73 Здесь ученики первый раз знакомятся с записью
- 122. Программа И.И. Аргинской Е) Алгебраический материал М2А ч.2 с. 64
- 123. Алгебраический материал М2А ч.2 с.72
- 124. Алгебраический материал М3А ч.2 с.22
- 125. Алгебраический материал М4А ч.2 с.23
- 126. Вывод: По программе Моро учащимся предлагаются уже готовые алгоритмы, выучив которые они могут применять их при
- 127. Тема «Алгоритм» в разных программах: По программе Петерсон во 2 классе вводится тема «Программы с вопросами»,
- 129. Скачать презентацию






















































































































 Симметрия. Виды симметрии
Симметрия. Виды симметрии Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Геометрические тела. Построение плоских срезов на геометрических телах
Геометрические тела. Построение плоских срезов на геометрических телах Базис и координаты
Базис и координаты Степень числа
Степень числа Формулы приведения
Формулы приведения Известное и неизвестное о квадратном трёхчлене
Известное и неизвестное о квадратном трёхчлене Задачи на готовых чертежах: Перпендикулярность плоскостей
Задачи на готовых чертежах: Перпендикулярность плоскостей Опорная сеть памяти (ОСП) – таблица сложения
Опорная сеть памяти (ОСП) – таблица сложения Построение графиков функций. Алгебра и начала анализа 11 класс
Построение графиков функций. Алгебра и начала анализа 11 класс Методы оценки рисков проекта
Методы оценки рисков проекта Подобные треугольники. (8 класс)
Подобные треугольники. (8 класс) Вычисление плошади поверхности многраников
Вычисление плошади поверхности многраников Периметр
Периметр Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики
Сложение и вычитание с переходом через десяток в пределах 10. Интерактивная игра-тренажер по математике Смешарики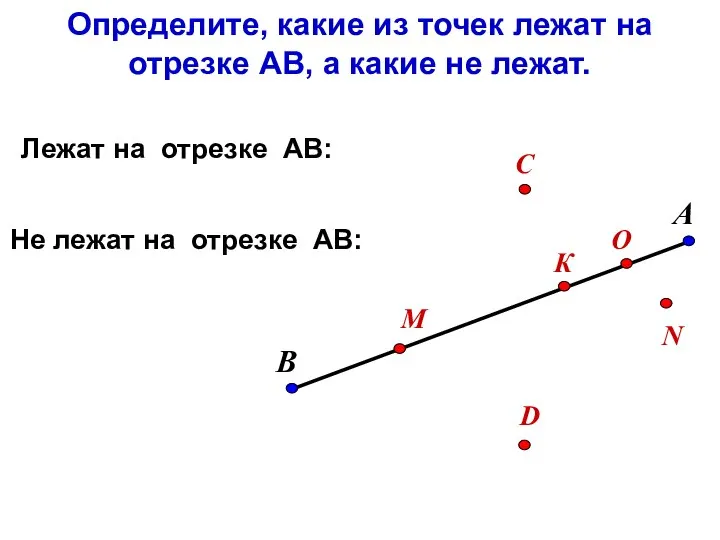 Отрезок. Длина отрезка
Отрезок. Длина отрезка Задачи на построение. 7 класс
Задачи на построение. 7 класс Презентация на тему О числах
Презентация на тему О числах  Презентация на тему Прибавление числа к сумме (1 класс)
Презентация на тему Прибавление числа к сумме (1 класс)  Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис
Тема урока: Десятичная система счисления Цели: Познакомиться с системами счисления. Сформировать умение работать с римскими чис Сколько раз в день минутная и часовая стрелки образуют прямую линию?
Сколько раз в день минутная и часовая стрелки образуют прямую линию? Презентация на тему Геометрия в жизни Многогранники 6 класс
Презентация на тему Геометрия в жизни Многогранники 6 класс  Интервальное оценивание параметров распределения случайных величин. Доверительный интервал
Интервальное оценивание параметров распределения случайных величин. Доверительный интервал Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Шар. Сфера
Шар. Сфера Кривая Лоренца. Решение задач
Кривая Лоренца. Решение задач Построение графика функции с помощью производной
Построение графика функции с помощью производной