Содержание
- 2. Определение иррациональности С философской точки иррациональность – недоступность рассудку, то, что не может быть постигнуто разумом,
- 3. Определение иррациональности С математической точки иррациональность – несоизмеримость с единицей; не является ни целой, ни дробной
- 4. Греческий математик Евклид в 3 веке до н.э. создал первую математическую школу. Первое научное определение числа
- 5. Л.Ф. Магницкий (1703 году) – создал первый учебник арифметики в России. «Единица есть то, в соответствии
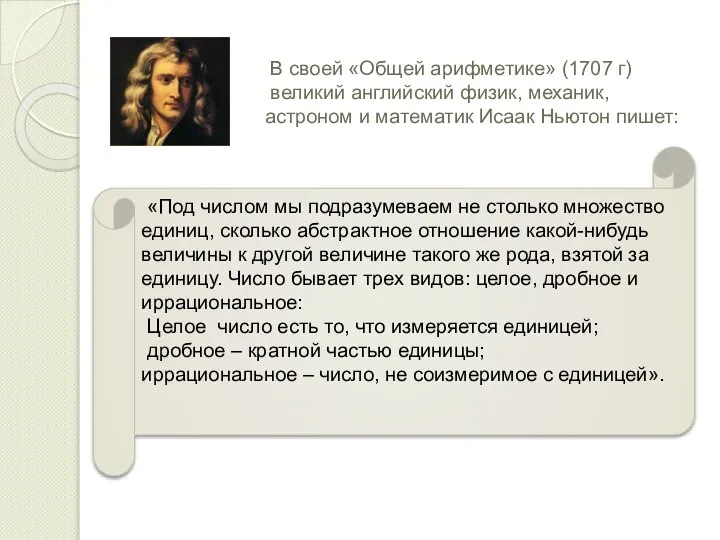
- 6. В своей «Общей арифметике» (1707 г) великий английский физик, механик, астроном и математик Исаак Ньютон пишет:
- 7. « Без знания дробей никто не может признаваться сведущим в арифметике». В начале XVIII столетия существовало
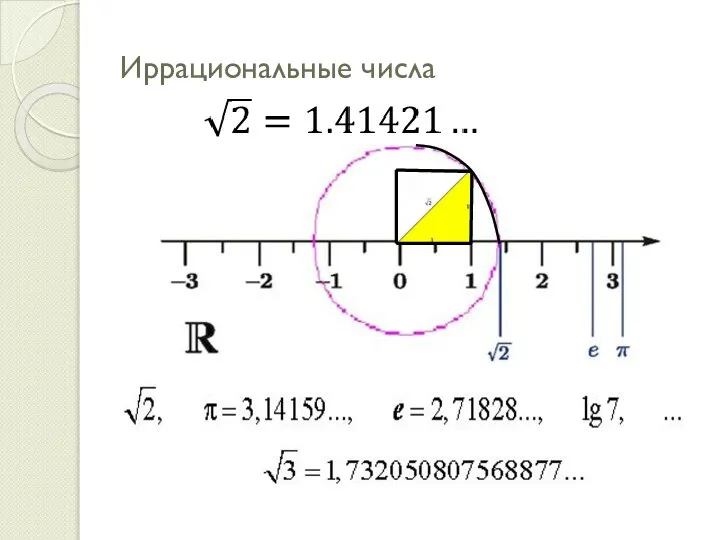
- 8. Иррациональные числа
- 9. Как доказать, что число иррационально?
- 10. Человеку часто приходиться сталкиваться с иррациональными числами.
- 11. Справочные сведения:
- 12. Справочные сведения
- 13. Справочные сведения
- 14. Паоло Руффини — итальянский математик (1765—1822), доктор медицины; первый доказал невозможность решения в радикалах всех уравнений
- 15. Справочные сведения
- 17. Заключение «Числа управляют миром», – говорили пифагорейцы. Мы не можем согласиться с данным утверждением, мы знаем,
- 19. Скачать презентацию








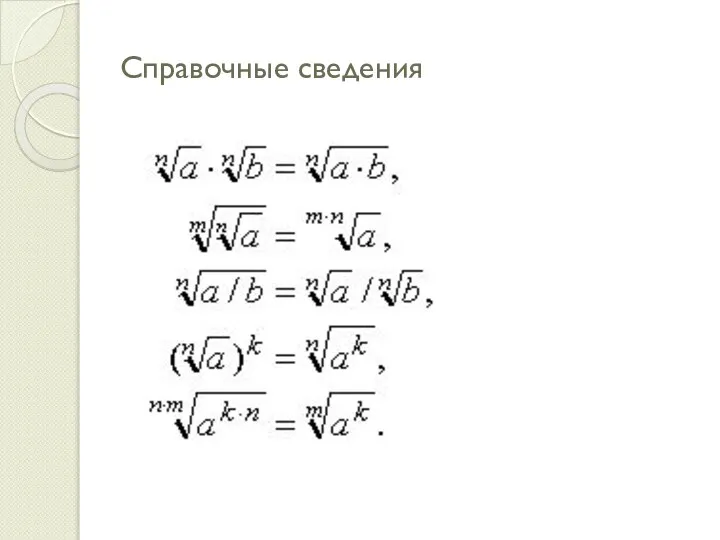





 Lecture 7
Lecture 7 Детерминационный, факторный и кластерный анализ
Детерминационный, факторный и кластерный анализ арифметическая прогрессия. Решение задач. 9 класс
арифметическая прогрессия. Решение задач. 9 класс Решение задач
Решение задач Повторение пройденного материала
Повторение пройденного материала Квадратичная функция (8 класс)
Квадратичная функция (8 класс) Одночлен и его стандартный вид
Одночлен и его стандартный вид Свойства умножения. 5 класс
Свойства умножения. 5 класс Пропорция. Основное свойство пропорции
Пропорция. Основное свойство пропорции Кубические см
Кубические см Показательная функция
Показательная функция Производная и исследование функции
Производная и исследование функции Открытый банк заданий ЕГЭ по математике
Открытый банк заданий ЕГЭ по математике Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10)
Статистическая теория радиотехнических систем. Постановка задач и классификация методов приема сигналов. (Лекция 10) Презентация на тему Смежные углы
Презентация на тему Смежные углы  Доказательство тождеств, содержащих многочлен
Доказательство тождеств, содержащих многочлен Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Теория вероятностей. Лекция 4
Теория вероятностей. Лекция 4 Движение по окружности. Решение задач
Движение по окружности. Решение задач Цифровой образовательный ресурс. Приложение к урокам алгебры. 7 класс
Цифровой образовательный ресурс. Приложение к урокам алгебры. 7 класс Умозаключение по аналогии
Умозаключение по аналогии Исследование функции с помощью производной
Исследование функции с помощью производной Четырехугольники
Четырехугольники Квадратное уравнение и его корни. Решение полных квадратных уравнений
Квадратное уравнение и его корни. Решение полных квадратных уравнений Разложение вектора по трём некомпланарным векторам
Разложение вектора по трём некомпланарным векторам Сложение вида +2, +3
Сложение вида +2, +3 Цилиндр
Цилиндр Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц
Составление и решение текстовых задач на увеличение и уменьшение числа на несколько единиц