Содержание
- 2. Содержание Понятие первообразной Неопределенный интеграл Таблица первообразных Три правила нахождения первообразных Определенный интеграл Вычисление определенного интеграла
- 3. Понятие первообразной Функцию F(x) называют первообразной для функции f(x) на интервале (a; b), если на нем
- 4. Примеры f(x) = 2x; F(x) = x2 F′(x)= (x2)′ = 2x = f(x) f(x) = –
- 5. Неопределенный интеграл Неопределенным интегралом от непрерывной на интервале (a; b) функции f(x) называют любую ее первообразную
- 6. Примеры
- 7. Таблица первообразных f(x) F(x) F(x)
- 8. Три правила нахождения первообразных 1º Если F(x) есть первообразная для f(x), а G(x) – первообразная для
- 9. Физический смысл первообразной
- 10. Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен
- 11. Вычисление определенного интеграла
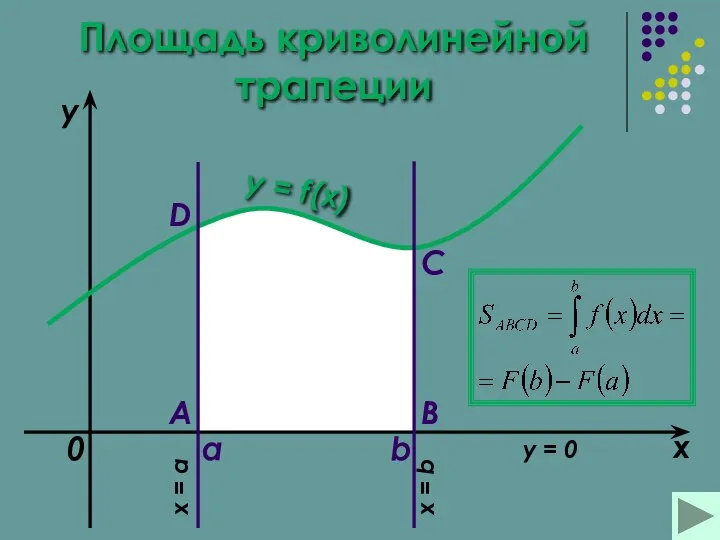
- 12. Площадь криволинейной трапеции a b x y y = f(x) 0 A B C D x
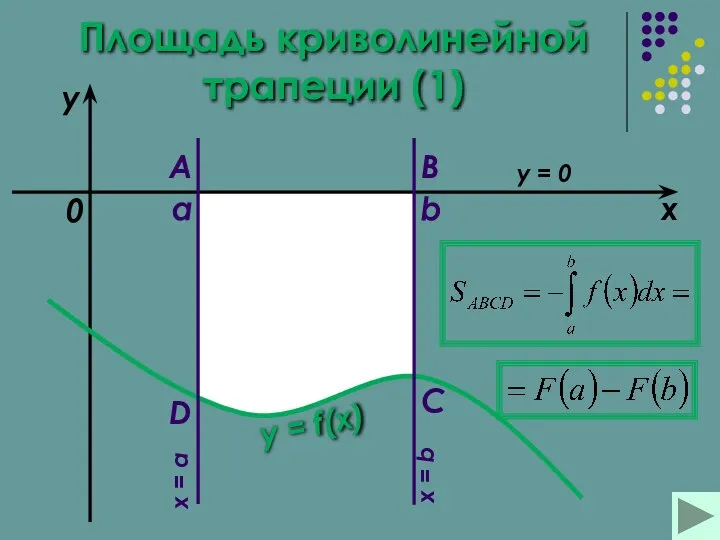
- 13. Площадь криволинейной трапеции (1) a b x y y = f(x) 0 A B C D
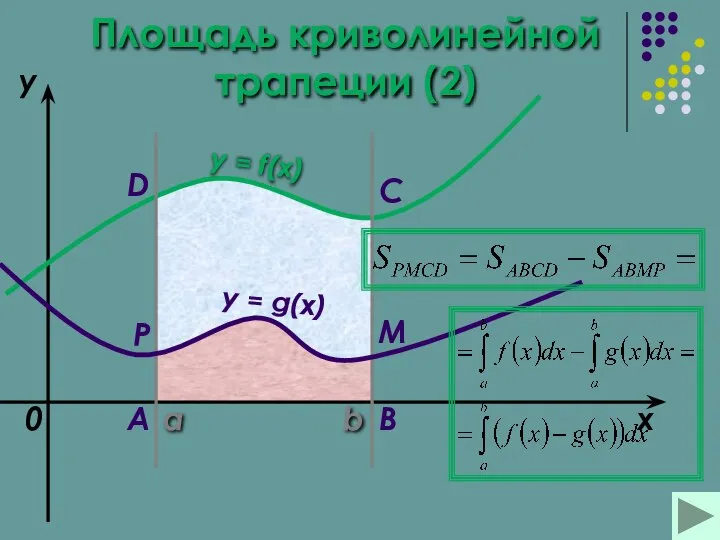
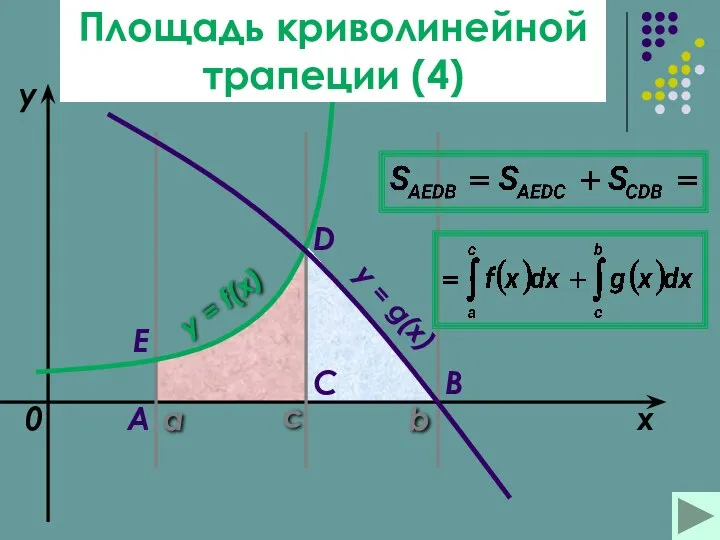
- 14. a b x y y = f(x) 0 y = g(x) A B C D M
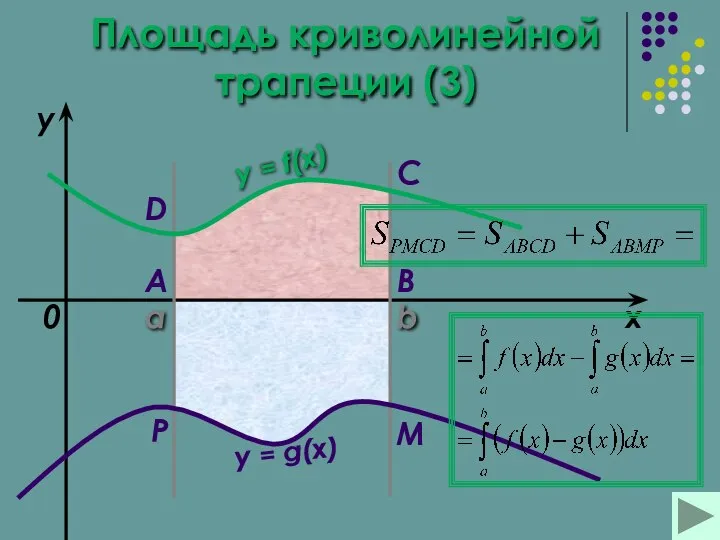
- 15. a b x y y = f(x) 0 y = g(x) A B C D M
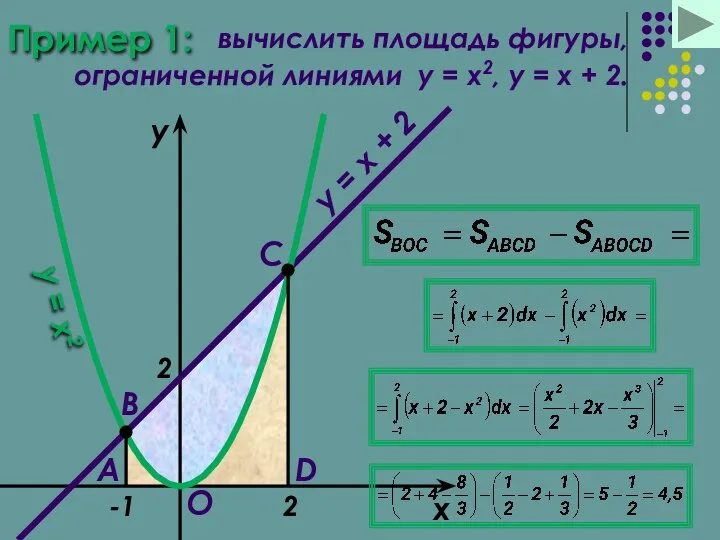
- 16. Пример 1: вычислить площадь фигуры, ограниченной линиями y = x2, y = x + 2. x
- 17. a b x y y = f(x) 0 y = g(x) A B C D с
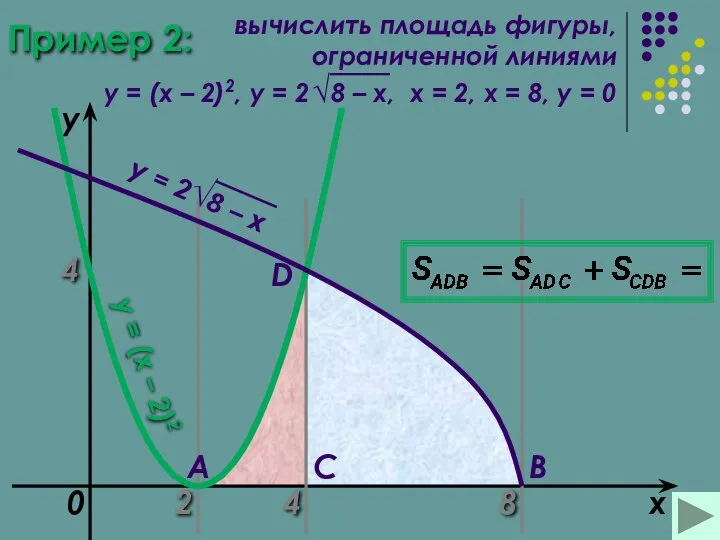
- 18. Пример 2: 2 8 x y = (x – 2)2 0 A B C D 4
- 20. Скачать презентацию










 Презентация на тему Теорема Виета
Презентация на тему Теорема Виета  Гипотенуза и катеты в треугольнике. Задачи
Гипотенуза и катеты в треугольнике. Задачи Математика. Проверочная работа
Математика. Проверочная работа Графическое решение задач
Графическое решение задач Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике Преобразование в плоскости. Методика изучения симметрии в начальной школе
Преобразование в плоскости. Методика изучения симметрии в начальной школе Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Простые и составные числа
Простые и составные числа Решение иррациональных уравнений
Решение иррациональных уравнений Цифра 8
Цифра 8 Игра Жизнь Conway's Game of Life
Игра Жизнь Conway's Game of Life Математическая викторина
Математическая викторина Решение систем уравнений
Решение систем уравнений Правила вычисления производной
Правила вычисления производной Предсказание будущего
Предсказание будущего Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Сумма углов треугольника
Сумма углов треугольника Расстояние между точками
Расстояние между точками Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Сумма углов треугольника
Сумма углов треугольника Задания для домашнего обучения
Задания для домашнего обучения Интерполирование полиномами Ньютона
Интерполирование полиномами Ньютона Таблица сложения
Таблица сложения Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов
Просто, сложно, интересно. Учебный курс предпрофильной подготовки для учащихся 9-х классов Обыкновенные дроби. Основное свойство дроби. 5 класс
Обыкновенные дроби. Основное свойство дроби. 5 класс Двоичная арифметика
Двоичная арифметика Золотое сечение и гармония форм природы и искусства. 8 класс
Золотое сечение и гармония форм природы и искусства. 8 класс Презентация по математике "Дроби на Руси" -
Презентация по математике "Дроби на Руси" -