Теория вероятностей. Равновероятные возможности

Цели
образовательные: рассказать о значении понятия теории вероятностей; объяснить понятия равновероятных величин, частоты случайного события;
воспитательные: владение интеллектуальными умениями и мыслительными операциями;
развивающие: развивать умение отличать равновероятные возможности от неравновероятных, приводить примеры различных возможностей.

План урока
Организационный момент;
Устная работа;
О теории вероятностей;
Объяснение нового материала;
Формирование умений и навыков;
Итоги урока;
Домашнее задание.

Разложите на множители

Еще первобытный вождь понимал, что у десятка охотников «вероятность» поразить копьем зубра гораздо больше, чем у одного. Поэтому и охотились тогда коллективно.

Неосновательно было бы думать, что такие древние полководцы, как Александр Македонский или Дмитрий Донской, готовясь к сражению, уповали только на доблесть и храбрость воинов.
Несомненно, они на основании наблюдений и опыта военного руководства умели как-то оценить «вероятность» своего возвращения «со щитом» или «на щите», знали, когда принимать бой, когда уклониться от него. Они не были рабами случая, но вместе с тем они были еще очень далеки от теории вероятностей. А ведь именно теория вероятностей помогает спрогнозировать некоторые ситуации.

Люди часто попадают в ситуации, в которых нужно выбрать из двух равноценных вариантов. На помощь часто приходит монетка, одна сторона которой называется «орлом», а другая «решкой». Подбросив такую монетку, знаем, что есть всего две равноправные или равновероятные возможности.

Что же изучает такой раздел математики, как «теория вероятности»?
Она отмечает закономерности случайных событий и величин. Впервые данным вопросом заинтересовались ученые еще в восемнадцатом веке, когда изучали азартные игры. Основное понятие теории вероятности – событие.

События
Основное понятие теории вероятности – это событие.
Все они делятся на следующие категории:
Достоверные
Невозможные
Случайные
Теория вероятности –
это наука, изучающая
возможность выпадения
какого-либо события.

ДОСТОВЕРНЫЕ события
Мы работаем и получаем вознаграждение в виде заработной платы.
Мы вложили деньги в банк, при необходимости получим их назад.
Такие события являются достоверными.
Если мы выполнили все необходимые условия, то обязательно получим ожидаемый
результат.

НЕВОЗМОЖНЫЕ события
Вода замерзла при температуре плюс десять (это невозможно).

СЛУЧАЙНЫЕ события

Сколько вариантов выпадения очков возможно при бросании одной игральной кости?
Равноправны ли эти варианты?

ЗАДАЧА № 1:
Сколько вариантов выпадения очков возможно при бросании одной игральной кости? Равноправны ли эти варианты?

ЗАДАЧА № 2:
В колоде 36 карт. Из нее наугад вытаскивают одну карту.
Сколько при этом имеется разных возможностей?
Равноправны ли возможности:
а) вытащить десятку бубен и вытащить пиковую даму;
б) вытащить валета и вытащить короля;
в) вытащить туза и вытащить какую-нибудь карту бубновой масти?
Если нет, то какая из этих возможностей более вероятна?

ЗАДАЧА № 3:
Из коробки, в которой лежат 6 бильярдных шаров с номерами от 1 до 6, наугад вытаскивают один шар. Сколько существует возможностей вытащить шар?
Равноправны ли возможности вытащить черный и красный шары, если в коробке:
а) 3 черных и 3 красных шара;
б)2 черных и 4 красных шара?
Если нет, то какая из этих возможностей более вероятна?

ВТОРОЙ УРОК ПО ТЕМЕ
« РАВНОВЕРОЯТНЫЕ ВОЗМОЖНОСТИ»

КАКИЕ ВИДЫ СОБЫТИЙ ВЫ ЗНАЕТЕ?

ПРОВЕРЬ СЕБЯ!!!
№ 1. Одновременно бросают две монеты.
Какие при этом возможности выпадения монет?
Равновероятны ли эти возможности?

ПРОВЕРЬ СЕБЯ!!!
№ 2. Бросают игральный кубик.
Какое событие более вероятно:
выпадение четного или нечетного числа очков?

ПРОВЕРЬ СЕБЯ!!!
№ 3. Одновременно бросают два игральных кубика. Какие суммы очков могут выпасть?
Равновероятны ли возможности выпадения этих сумм?

ПРОВЕРЬ СЕБЯ!!!
№ 4. Бросают игральный кубик.
Какое событие более вероятно:
выпадение числа очков суммы больше четырех или меньше четырех?

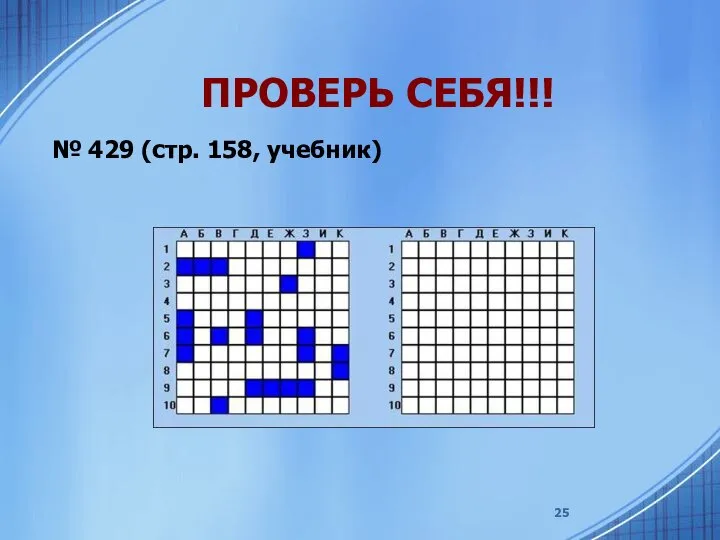
ПРОВЕРЬ СЕБЯ!!!
№ 429 (стр. 158, учебник)

ПРОВЕРЬ СЕБЯ!!!
На десяти карточках записаны целые числа от 0 до 9. Наугад выбирают две карточки и находят сумму записанных на них чисел. Равновероятны ли возможности получить в сумме число от 1 до 9? Если нет, то какая сумма более вероятна?