Построение и анализ параллельных алгоритмов

Модель PRAM
Модель PRAM: Parallel Random-Access Memory
Позволяет учитывать ограничения, связанные с одновременным доступом к памяти
Является идеализированной моделью архитектуры SMP (Symmetric MultiProcessor, Shared Memory Processor)

Модель PRAM
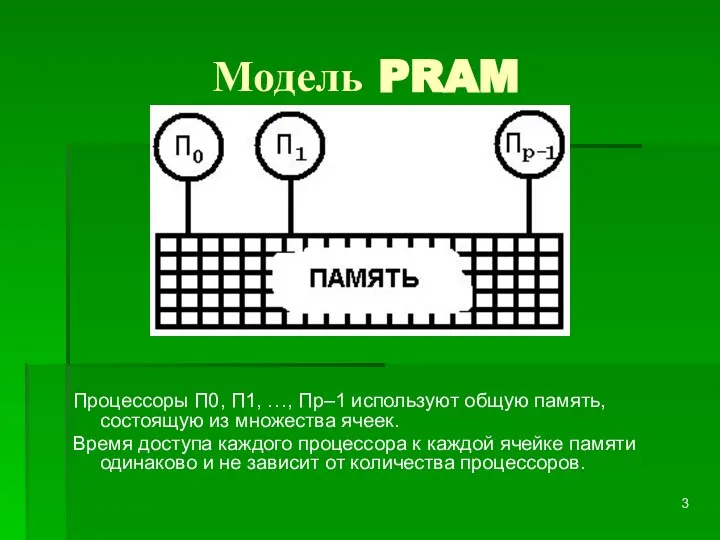
Процессоры П0, П1, …, Пp–1 используют общую память, состоящую из множества ячеек.
Время доступа каждого процессора к каждой ячейке памяти одинаково и не зависит от количества процессоров.

Модель PRAM
Один шаг (такт) работы PRAM-машины синхронизирован по фазам:
Чтение данных из памяти.
Обработка данных.
Запись результата в память.

Режимы чтения и записи
Режимы чтения данных из памяти:
Одновременное (Concurrent Read)
Исключающее (Exclusive Read)
Режимы записи в память:
Одновременная (Concurrent Write)
Исключающая (Exclusive Write)

Варианты одновременной записи
Одновременная запись одинакового значения
Произвольная запись: сохраняется произвольное значение из множества записываемых
Запись в зависимости от приоритетов процессоров
Комбинация записываемых значений

Виды PRAM машин и алгоритмов

ЗАДАЧА НАХОЖДЕНИЯ КОРНЕЙ ДВОИЧНОГО ЛЕСА
Пример CREW-алгоритма

Пример CREW-алгоритма
Дано: Лес, состоящий из бинарных деревьев. Деревья заданы следующим образом: для каждой вершины имеется указатель на её родителя. Для корней деревьев этот указатель пуст.
Требуется: для каждой вершины найти корень дерева, которому она принадлежит

Пример CREW-алгоритма
Представление входных данных:
вершины пронумерованы,
ребра деревьев заданы с помощью массива parent: элемент parent[i] представляет номер вершины, являющейся родителем для вершины с номером i.

Пример CREW-алгоритма
Результат работы алгоритма — массив root. В ячейке root[i] хранится вершины, являющейся корнем дерева, в которое входит вершина i.
Массивы parent и root хранятся в общей памяти.

CREW-алгоритм
Для каждого процессора Pi выполнить
Если parent[i] = NIL, то root[i] := i;
Пока существует узел i, для которого parent[i] ≠ NIL, выполнять:
Для каждого процессора i выполнить
Если parent[i] ≠ NIL, то
{
root[i] := root[parent[i]];
parent[i] := parent[parent[i]];
}

Анализ CREW-алгоритма
Временная сложность алгоритма:
O(log2 d),
где d — наибольшая глубина дерева в заданном лесе.
Можно показать, что ни один EREW-алгоритм не может решить эту задачу за время, меньшее O(log2 n), где n — количество вершин в лесе

НАХОЖДЕНИЕ МАКСИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕ
Пример CRCW-алгоритма

Пример CRCW-алгоритма
Дано: Массив n элементов
Требуется: Найти максимальный элемент

Пример CRCW-алгоритма
Способ решения
Количество процессоров: n2.
Каждый процессор нумеруется парой индексов.
Процессор с номером (i,j) сравнивает A[i] и A[j].
Используется вспомогательный булевский массив m[i]. После выполнения сравнений m[i]=true ⇔ A[i] — наибольший элемент массива.
Результат помещается в переменную max.

CRCW-алгоритм
Для всех i от 0 до n–1 выполнить:
m[i] := true;
Для всех i от 0 до n–1 и для всех j от 0 до n–1 выполнить:
Если A[i] < A[j], то m[i] := false;
Для всех i от 0 до n–1 выполнить:
Если m[i] = true, то max := A[i];
Вернуть max.

Анализ CRCW-алгоритма
Без использования параллельного чтения невозможно решить эту же задачу быстрее, чем за время O(log n).
Представленный CRCW-алгоритм работает за время O(1) и требует n2 процессоров. Наилучший последовательный алгоритм работает за время O(n). Поэтому эффективность составляет 1/n, т.е. алгоритм не является эффективным по затратам.