Содержание
- 2. Для каждого из событий определите, каким оно является – невозможным, достоверным или случайным: Из промежутка [1;5]
- 3. Противоположное событие. Событие Ā называют противоположным событию А, если событие Ā происходит тогда и только тогда,
- 4. Примеры противоположных событий: «Ясный день» – «дождливый день»; «Выпал орел» – «выпала решка» , противоположные события
- 5. Назовите событие, противоположное данному: В результате броска игральной кости выпало число, равное 2; В результате броска
- 6. Совместные и несовместные события. Два события А и В называют совместными, если они могут произойти одновременно,
- 7. Укажите совместность – несовместность случайных событий: 1) Катя со Славой играли в шахматы. А – «Катя
- 8. Комбинации событий. Суммой (объединением) событий А и В называется событие, которое состоит в том, что происходит
- 9. Сумма событий. Пример. Если испытание состоит в определении числа на верхней грани игрального кубика после одного
- 10. Комбинации событий. Произведением (пересечением) событий А и В называется событие, которое состоит в том, что происходят
- 11. Произведение событий. Пример. Если событие А – выпадение четного числа, а событие В – выпадение числа,
- 12. Комбинации событий. Из колоды карт наугад вынимают одну и рассматривают два события. А – вынута карта
- 13. Равносильные события. События А и В называют равными или равносильными и пишут А = В, если
- 14. Соотношения и связи между событиями можно изобразить с помощью кругов Эйлера. Автор метода - ученый Леонард
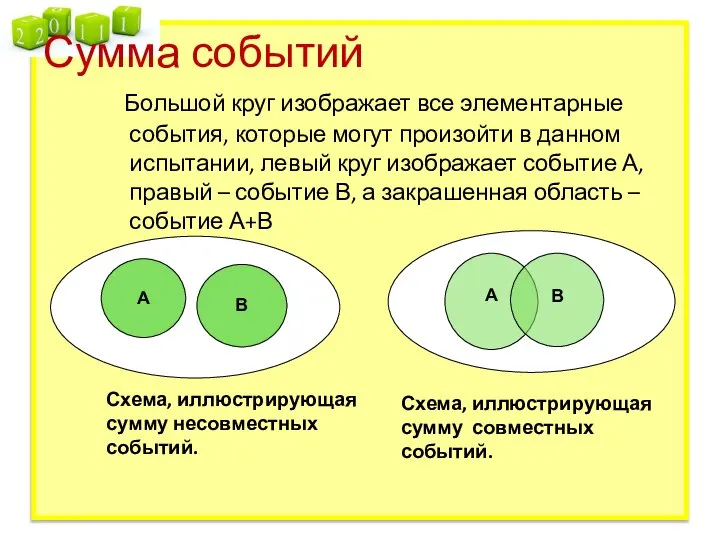
- 15. Сумма событий Большой круг изображает все элементарные события, которые могут произойти в данном испытании, левый круг
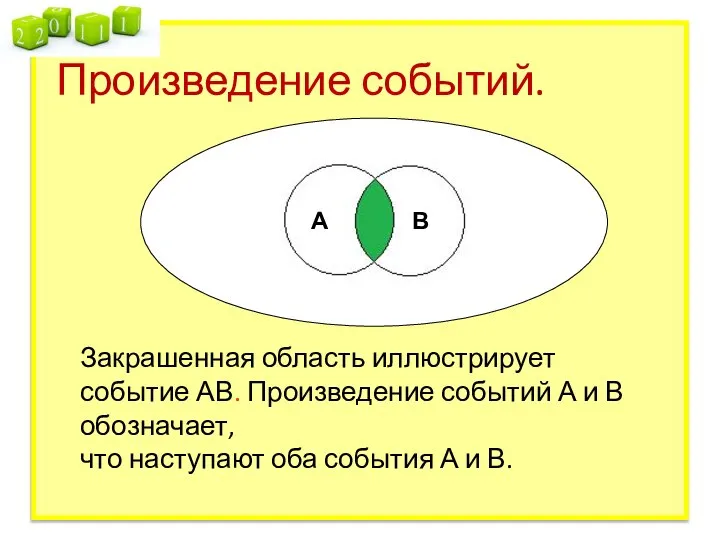
- 16. Произведение событий. Закрашенная область иллюстрирует событие АВ. Произведение событий А и В обозначает, что наступают оба
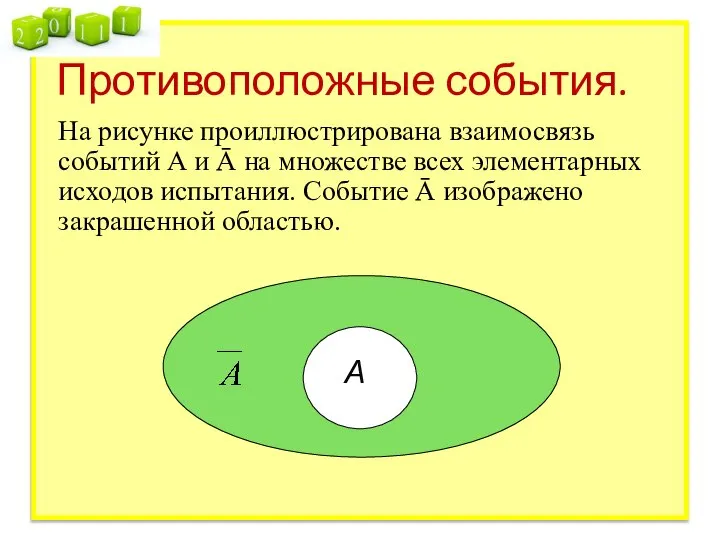
- 17. Противоположные события. На рисунке проиллюстрирована взаимосвязь событий А и Ā на множестве всех элементарных исходов испытания.
- 19. Скачать презентацию













 Урок по математике
Урок по математике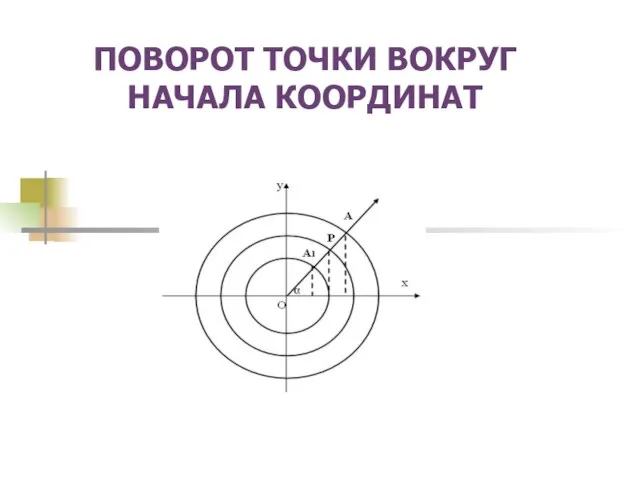 ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ
ПОВОРОТ ТОЧКИ ВОКРУГ НАЧАЛА КООРДИНАТ Применение производной к исследованию функций
Применение производной к исследованию функций Действия с дробями. Многогранники
Действия с дробями. Многогранники Введение в биоинформатику. Лекция 9
Введение в биоинформатику. Лекция 9 Решение задач. Диагностика 1
Решение задач. Диагностика 1 Презентация на тему Взаимно обратные функции
Презентация на тему Взаимно обратные функции  Материалы к урокам и факультативным занятиям для 11 класса
Материалы к урокам и факультативным занятиям для 11 класса Проценты. Ж.Ж. Руссо (1712–1778 гг.)
Проценты. Ж.Ж. Руссо (1712–1778 гг.) Суждение, как форма мышления. Классификация
Суждение, как форма мышления. Классификация Площадь многоугольника
Площадь многоугольника Осевая и центральная симметрии
Осевая и центральная симметрии Математика
Математика Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента
Обработка результатов измерений при прямых однократных измерениях. Математические методы планирования активного эксперимента Показательные уравнения
Показательные уравнения Умножение и деление натуральных чисел
Умножение и деление натуральных чисел Формулы сложения
Формулы сложения Формула Ньютона-Лейбница. Площадь криволинейной трапеции
Формула Ньютона-Лейбница. Площадь криволинейной трапеции Угол между прямыми
Угол между прямыми Окружность и круг
Окружность и круг Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью
Ряды динамики. Виды рядов динамики и задачи, решаемые с их помощью Решение уравнений
Решение уравнений Числа по порялку
Числа по порялку Экзамен по математике
Экзамен по математике Тригонометрия. Базовые тригонометрические функции синус, косинус
Тригонометрия. Базовые тригонометрические функции синус, косинус Математика в логических упражнениях
Математика в логических упражнениях Графическое и табличное представление информации
Графическое и табличное представление информации