Теория вероятностей. Подготовка к ГИА

Случайное событие - это событие, которое либо произойдёт, либо нет.
Примеры:
Вы купили лотерейный билет. Он либо выигрышный, либо нет. Случайное событие - выигрыш. Оно может произойти, а может и нет.
Вы подбросили монету. Выпадение орла - случайное событие. Выпадение решки тоже случайное событие.
Студент сдаёт экзамен. Выпадение определённого билета – случайное событие. Сдаст или не сдаст тоже случайное событие.
СОБЫТИЯ

ИСХОДЫ
Испытание - любое действие, которое может привести к одному или нескольким результатам.
Исход - конечный результат испытания. Значит испытание может иметь один или несколько исходов.

Благоприятный исход - желаемый исход
Примеры:
Бросаете монету. Хочу, чтобы выпала решка, => благоприятный исход = выпала решка. Значит выпадение орла – неблагоприятный исход.
Сдаю экзамен. Из 20 билетов 10 знаю на отлично, 5 на хорошо, 3 на удовлетворительно и 2 не знаю. Хочу сдать на хорошо. Тогда благоприятный исход = сдать на хорошо. А какова вероятность сдать на хорошо?
Ответ: 5/20=1/4.

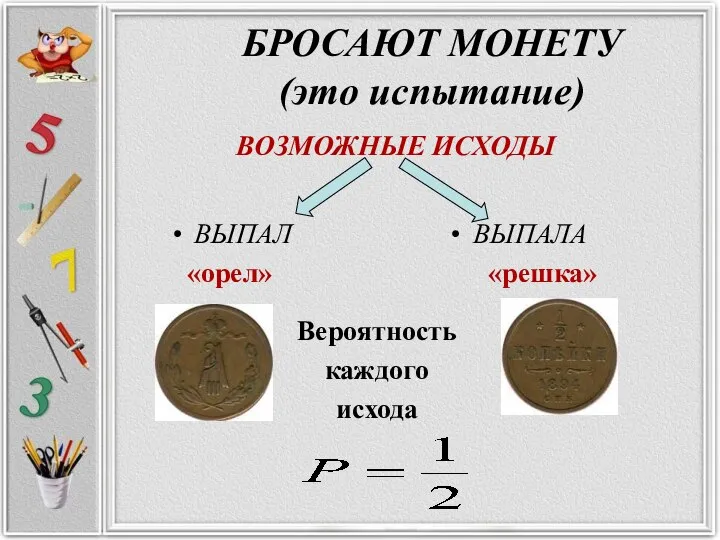
БРОСАЮТ МОНЕТУ
(это испытание)
ВЫПАЛ
«орел»
ВЫПАЛА
«решка»
ВОЗМОЖНЫЕ ИСХОДЫ
Вероятность
каждого
исхода

БРОСАЮТ ИГРАЛЬНУЮ КОСТЬ (испытание)
Выпало 1 очко
Выпало 2 очка
Выпало 3 очка
Выпало 4 очка
Выпало 5 очков
Выпало 6 очков
ВОЗМОЖНЫЕ ИСХОДЫ
6 возможных исходов
Загадали: «выпадет 3 очка»
ВЕРОЯТНОСТЬ этого события:

ФОРМУЛА ВЕРОЯТНОСТИ
Эта формула называется классической формулой вероятности или классическим определением вероятности. Где:
Р(А) – вероятность события А.
m – число (количество) благоприятных исходов,
n – число (количество) всех исходов.
ПРАВИЛО: Вероятность всегда равна от 0 до 1. Ни меньше, ни больше!

В МЕШКЕ 25 ЯБЛОК
7 красных
18 зеленых
Вероятность того, что из мешка достанут красное яблоко:
Вероятность того, что из мешка достанут зеленое яблоко:

РЕШАЕМ
В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
ЗАДАЧА № 1
РЕШЕНИЕ
0, 4
Всего возможных исходов 5;
Благоприятных исходов 2.

РЕШАЕМ
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
ВОЗМОЖНЫЕ ИСХОДЫ СОБЫТИЯ
ЗАДАЧА № 2
РЕШЕНИЕ
0, 5
О
О

РЕШАЕМ
На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
ЗАДАЧА № 3
РЕШЕНИЕ
0, 04
Число благоприятных исходов:
250-120-120 = 10;
Возможных: 250.

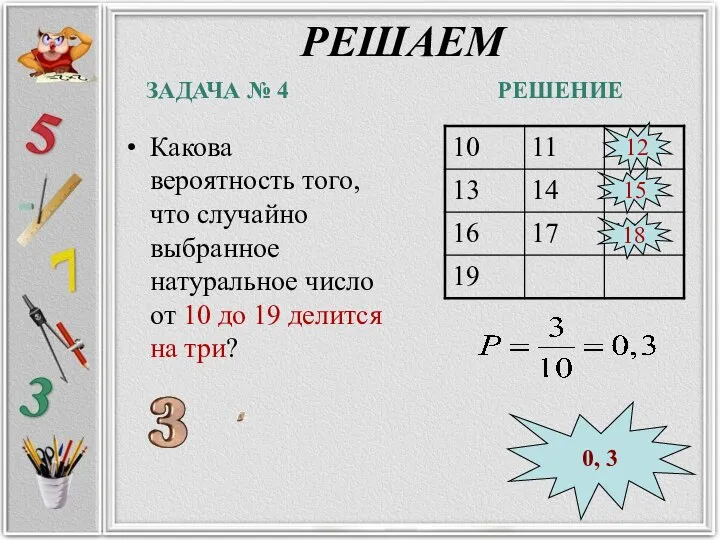
РЕШАЕМ
Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
ЗАДАЧА № 4
РЕШЕНИЕ
0, 3
12
15
18

РЕШАЕМ
В классе 26 человек, среди них два близнеца - Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
ЗАДАЧА № 5
РЕШЕНИЕ
Андрей в одной из групп
Всего исходов: 25 (не считаем Андрея)
Делят по 13 человек (среди них Андрей), т.е в группу, где находится Андрей, надо добавить только 12 человек
Благоприятных исходов: 12
0, 48

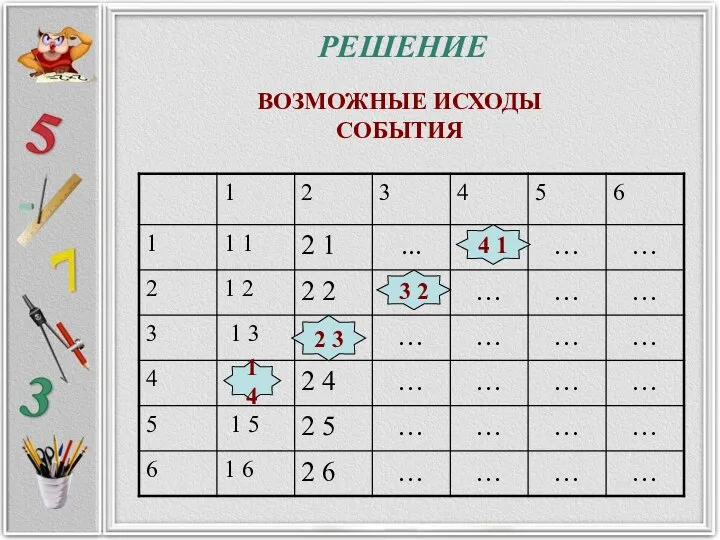
ЗАДАЧА № 6
РЕШАЕМ
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.

РЕШЕНИЕ
1 4
2 3
3 2
4 1
ВОЗМОЖНЫЕ ИСХОДЫ
СОБЫТИЯ

РЕШЕНИЕ
Всего возможных комбинаций при вбрасывании двух кубиков: 6 *6 = 36.
Из них благоприятные исходы можно перечислить:
Таким образом, всего благоприятных исходов 4.
Вероятность найдем, как отношение числа 4 благоприятных исходов к числу всех возможных комбинаций 36.
4/36 = 0,111111…
Округлим до сотых.
Ответ: 0, 11.

РЕШАЕМ
Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 спортсменов, среди которых 13 участников из России, в том числе Владимир Егоров. Найдите вероятность того, что в первом туре Владимир Егоров будет играть с каким-либо спортсменом из России?
ЗАДАЧА № 7

РЕШЕНИЕ
Всего 26 спортсменов. Среди них - Егоров, который сам с собой играть не может.
Следовательно: возможных исходов – 25.
13 участников из России, среди них Егоров. Следовательно: 12 партнеров из России.
0, 48

РЕШАЕМ
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Возможные исходы
ЗАДАЧА № 8
РЕШЕНИЕ
0, 25
1, 1, 1, 1
2, 2, 2, 2
3, 3, 3, 3
4, 4, 4, 4

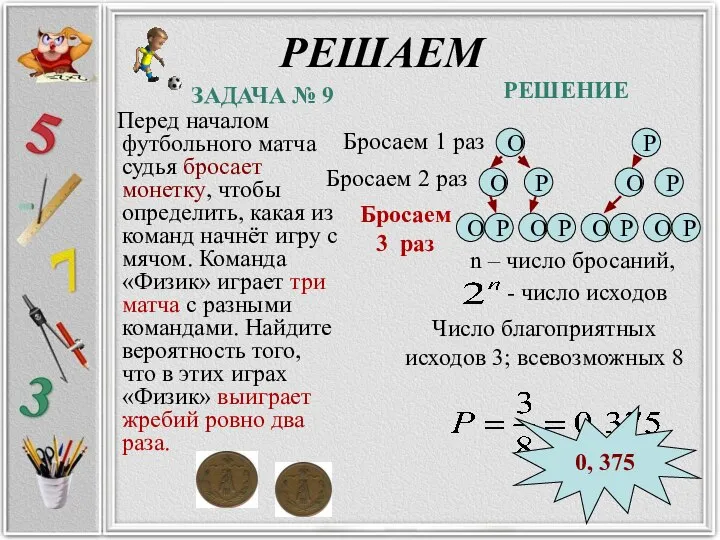
РЕШАЕМ
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
ЗАДАЧА № 9
РЕШЕНИЕ
О
Р
О
Р
О
Р
О
Р
О
Р
О
Р
О
Р
Бросаем 1 раз
Бросаем 2 раз
Бросаем 3 раз
n – число бросаний,
- число исходов
Число благоприятных исходов 3; всевозможных 8
0, 375

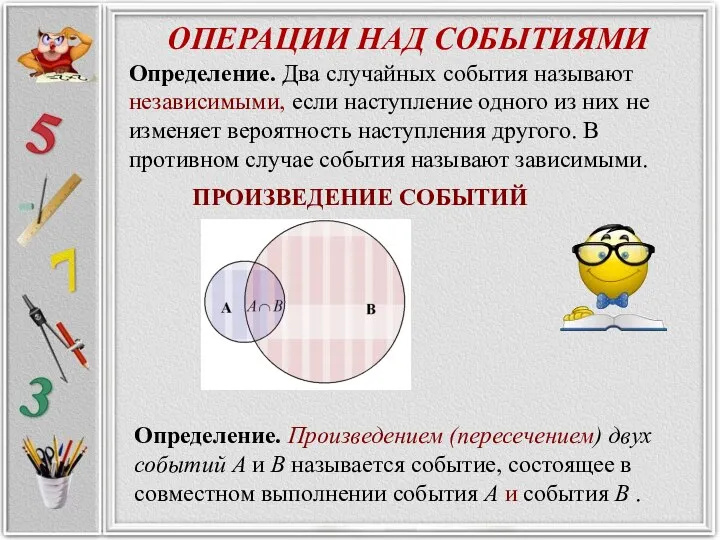
ОПЕРАЦИИ НАД СОБЫТИЯМИ
Фразу «наступит или событие А или событие В или оба события А и В» обычно заменяют фразой «наступит хотя бы (по крайней мере) одно из данных событий».
СУММА СОБЫТИЙ
Определение. События называют несовместными, если они не могут происходить одновременно в одном и том же испытании.
Для несовместных событий пересечения не будет (рис.).

ОПЕРАЦИИ НАД СОБЫТИЯМИ
ПРОИЗВЕДЕНИЕ СОБЫТИЙ
Определение. Произведением (пересечением) двух событий A и B называется событие, состоящее в совместном выполнении события A и события B .
Определение. Два случайных события называют независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события называют зависимыми.

ВЕРОЯТНОСТИ СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫТИЙ
Сумма вероятностей противоположных событий равна 1:

ПРИМЕРЫ
Вероятность, что при бросании игральной кости выпадет либо 3 очка, либо 4 очка.

ПРИМЕРЫ
Вероятность, того что молодой человек выиграет в лотерею 0, 01. А вероятность того, что он в этот же вечер познакомится с красивой девушкой 0,4. С какой вероятностью произойдут оба события?

РЕШАЕМ
Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
ЗАДАЧА № 10
РЕШЕНИЕ
0, 07

РЕШАЕМ
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
ЗАДАЧА № 11
РЕШЕНИЕ
0, 38

РЕШАЕМ
В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что все три продавца заняты равна:
ЗАДАЧА № 12
РЕШЕНИЕ
0, 027

РЕШАЕМ
Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
ЗАДАЧА № 13
РЕШЕНИЕ
0, 156

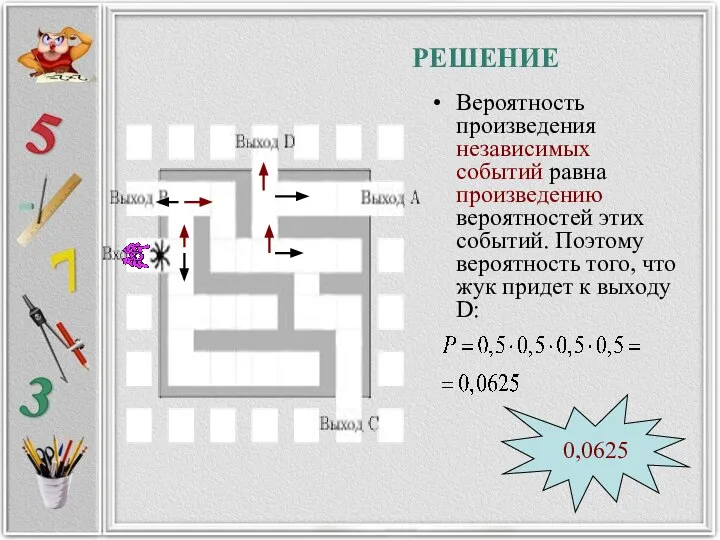
РЕШАЕМ
На рисунке изображен лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещеe не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придет к выходу D .
ЗАДАЧА № 14

РЕШЕНИЕ
Вероятность произведения независимых событий равна произведению вероятностей этих событий. Поэтому вероятность того, что жук придет к выходу D:
0,0625

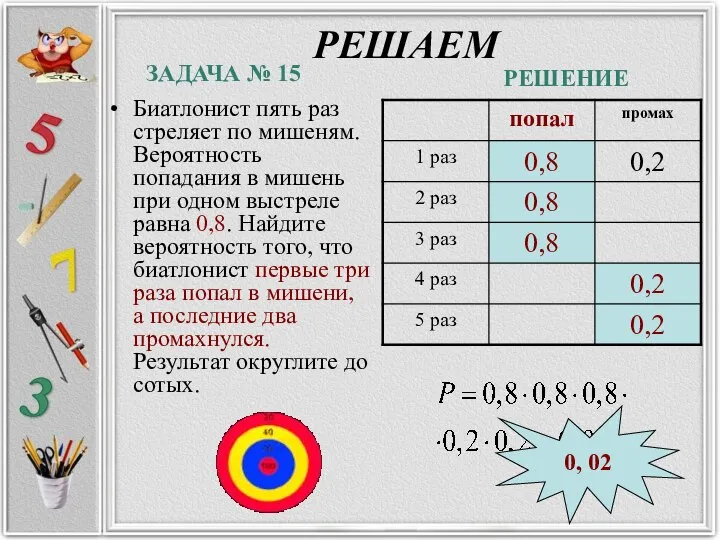
РЕШАЕМ
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
ЗАДАЧА № 15
РЕШЕНИЕ
0, 02

РЕШАЕМ
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая - 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая - 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
ЗАДАЧА № 16
РЕШЕНИЕ
0, 019

РЕШАЕМ
Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства - яйца высшей категории, а из второго хозяйства - 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.
ЗАДАЧА № 17
РЕШЕНИЕ
0, 75

РЕШАЕМ
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,07 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
ЗАДАЧА № 18
РЕШЕНИЕ
0, 9975
ВОЗМОЖНЫЕ ИСХОДЫ
+ -
- +
+ +
- -
Р=1

РЕШАЕМ
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
ЗАДАЧА № 19
РЕШЕНИЕ
Найдем вероятность того, что перегорят обе лампы. Эти события независимые, вероятность их произведения равно произведению вероятностей этих событий: 0,3·0,3 = 0,09.
Событие, состоящее в том, что не перегорит хотя бы одна лампа, противоположное. Следовательно, его вероятность равна: 1 − 0,09 = 0,91.
0, 91

РЕШАЕМ
ЗАДАЧА № 20
Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов - математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов - математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку - 0,8, по иностранному языку - 0,7 и по обществознанию - 0,5.
Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

РЕШАЕМ
Для того, чтобы поступить хоть куда-нибудь, З. нужно сдать и русский, и математику как минимум на 70 баллов, а помимо этого еще сдать иностранный язык или обществознание не менее, чем на 70 баллов.
РЕШЕНИЕ
и
ИСХОДЫ
+ -
- +
+ +
- -
0, 408

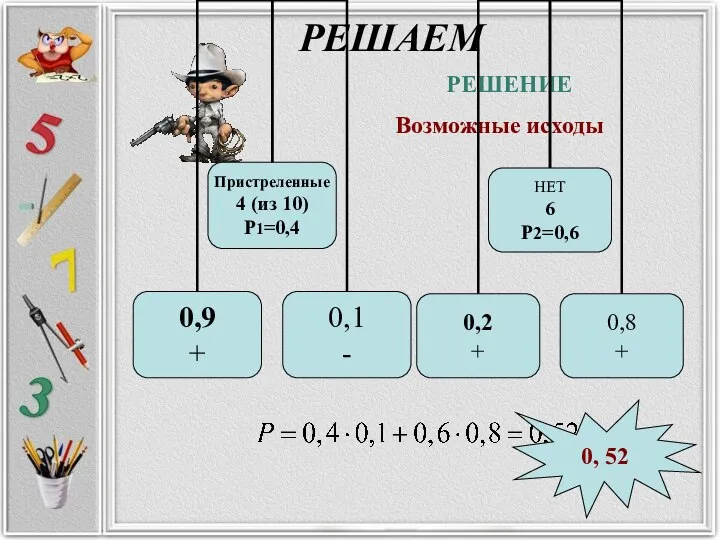
РЕШАЕМ
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
ЗАДАЧА № 21

РЕШАЕМ
Возможные исходы
РЕШЕНИЕ
0, 52

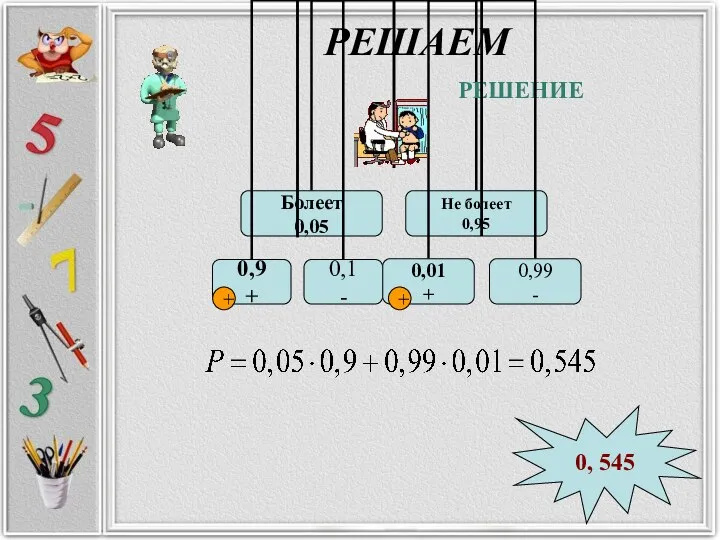
РЕШАЕМ
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
ЗАДАЧА № 22

РЕШАЕМ
РЕШЕНИЕ
0, 545
+
+

СОВМЕСТНЫЕ СОБЫТИЯ
События A и B совместные (зависимые), вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

РЕШАЕМ
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
ЗАДАЧА № 23
РЕШЕНИЕ
0, 12
Не равно произведению, т.к. события зависимые (совместные)
ИСХОДЫ
+ -
- +
- -
+ +
0, 52