Содержание
- 2. Биография Родился в Греции. Был математиком, учеником Евдокса Книдского. Являлся также членом Платоновской Академии. Рафаэль, «Афинская
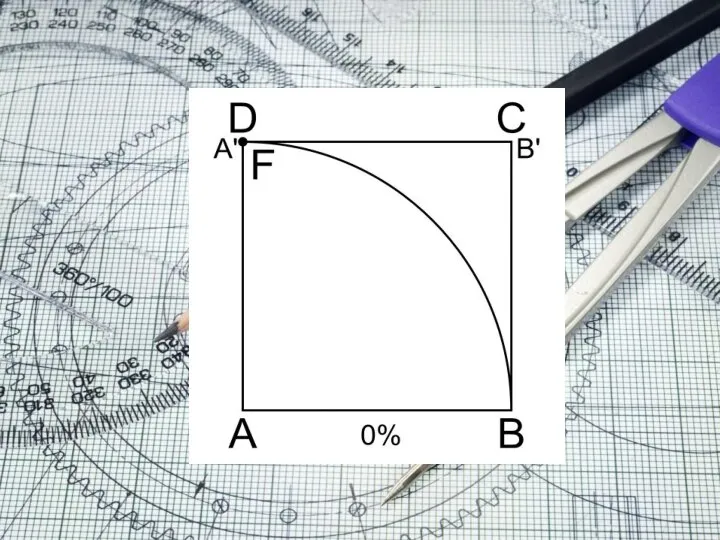
- 3. Решение задачи о квадратуре круга с помощью квадратрисы Пусть ANB — четверть окружности, расположенной в квадранте
- 5. Конические сечения Конические сечения — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей
- 6. Виды конических сечений Эллипс; гипербола; парабола.
- 7. Геометрическое обоснование первого замечательного предела Площадь треугольника AOB меньше площади сектора AOB, которая меньше площади прямоугольного
- 9. Скачать презентацию





 Измерение параллеппипеда
Измерение параллеппипеда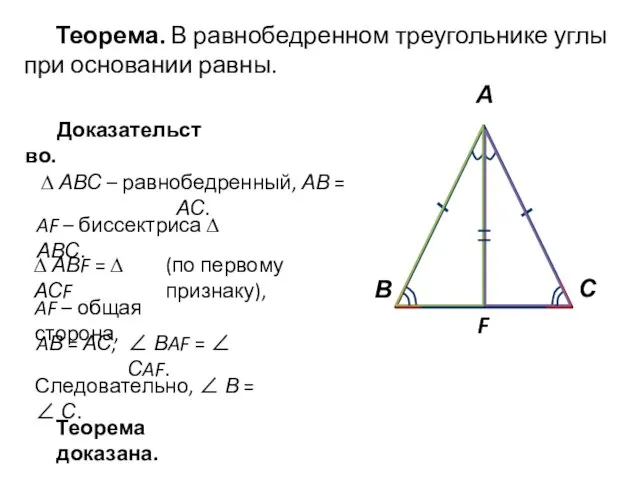 Теоремы к зачёту
Теоремы к зачёту Производная сложной функции
Производная сложной функции Система быстрого счёта в уме Якова Трахтенберга. Занятия 3
Система быстрого счёта в уме Якова Трахтенберга. Занятия 3 Теремок цифр. Сказка для детей 5-9 лет
Теремок цифр. Сказка для детей 5-9 лет Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13
Metode numerice. Mulţimea F, de numere în virgulă mobilă este. Curs13 Матрицы и определители
Матрицы и определители Масштаб чертежа
Масштаб чертежа Иррациональные уравнения и их системы
Иррациональные уравнения и их системы Треугольники. Виды треугольников. Теорема о равенстве двух треугольников
Треугольники. Виды треугольников. Теорема о равенстве двух треугольников Тренировочные задания В2 (графическое представление данных)
Тренировочные задания В2 (графическое представление данных) Неопределенный интеграл
Неопределенный интеграл Задачи на нахождение площади прямоугольника и трапеции
Задачи на нахождение площади прямоугольника и трапеции Уравнения! Реформа образования
Уравнения! Реформа образования Презентация на тему Формирование и развитие УУД на уроках математики
Презентация на тему Формирование и развитие УУД на уроках математики  Прямоугольный параллелепипед
Прямоугольный параллелепипед Тема 4. Производная функции
Тема 4. Производная функции Число пи вокруг нас
Число пи вокруг нас Правильные многоугольники
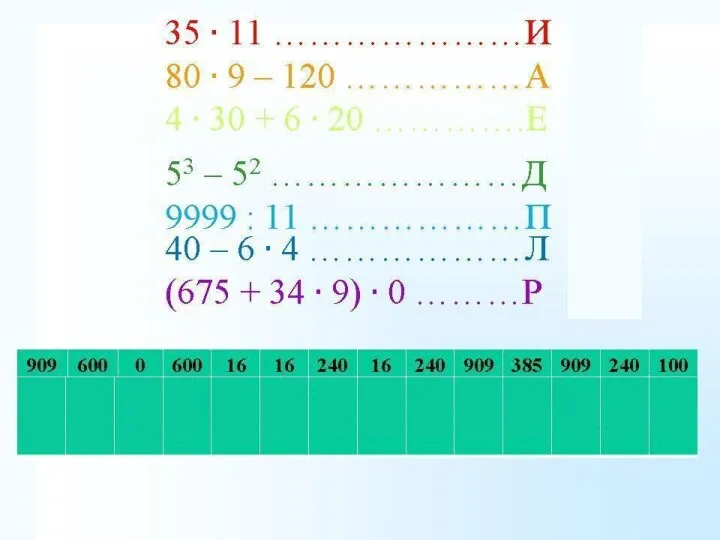
Правильные многоугольники Сочетательное свойство умножения
Сочетательное свойство умножения Многоугольники
Многоугольники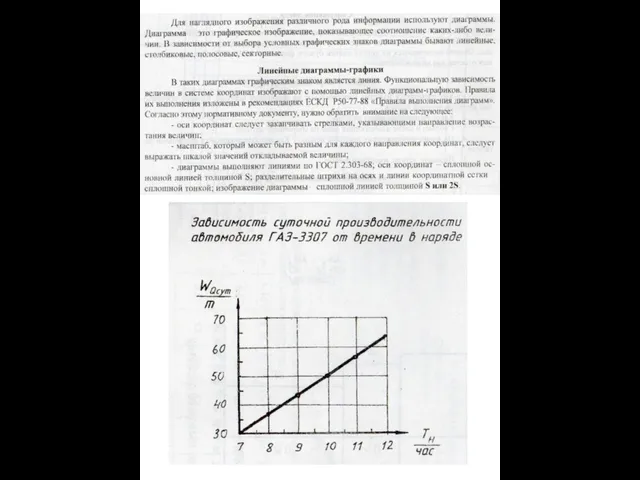 Графики и диаграммы
Графики и диаграммы Презентация на тему Умножение и деление десятичных дробей на натуральные числа
Презентация на тему Умножение и деление десятичных дробей на натуральные числа  Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Презентация на тему ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ  Многочлен. Основные понятия. Определение многочлена
Многочлен. Основные понятия. Определение многочлена Определённый интеграл
Определённый интеграл Решение задач
Решение задач Функция у = √х, ее свойства и график
Функция у = √х, ее свойства и график