Слайд 4Литература
Szd_Analyzdann_bBi_17.pdf

Слайд 5Регрессионный анализ
В зависимости от количества факторов, включенных в регрессию, принято различать регрессию

простую и множественную.
Простая регрессия представляет собой регрессию между двумя переменными (y и x), т.е. рассматривается модель вида: y=f(x)
Множественная регрессия соответственно представляет сбой регрессию результирующего признака с двумя и большим числом факторов, т.е. рассматривается модель y=f(x1,x2,x3,…)
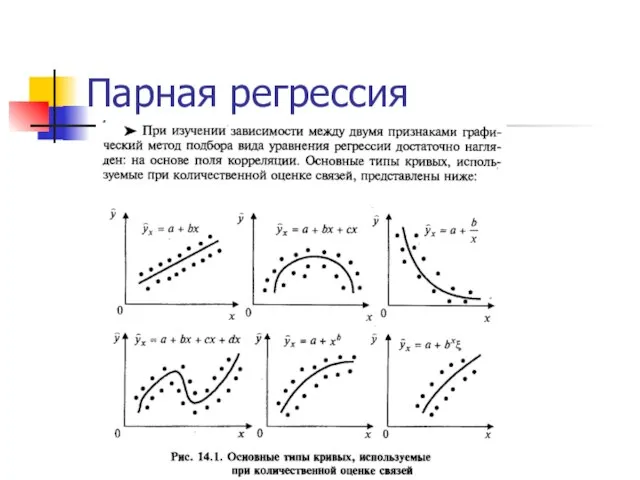
Слайд 12Парная линейная регрессия и корреляция

Слайд 13Парная линейная регрессия и корреляция

Слайд 14Парная линейная регрессия и корреляция
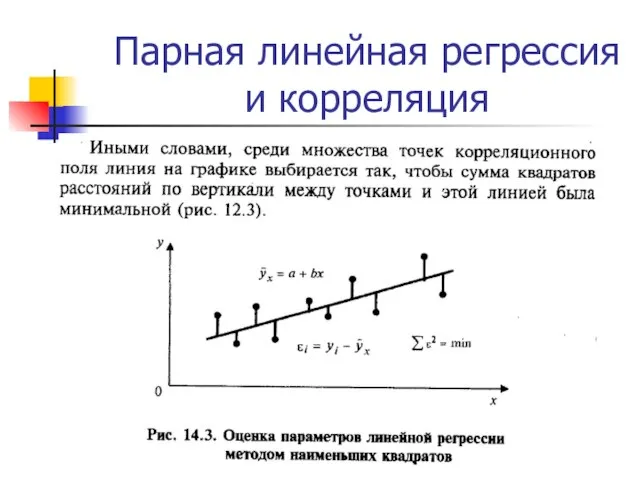
Слайд 15Парная линейная регрессия и корреляция

Слайд 16Парная линейная регрессия и корреляция

Слайд 17Парная линейная регрессия и корреляция

Слайд 18Парная линейная регрессия и корреляция

Слайд 19Парная линейная регрессия и корреляция

Слайд 20Парная линейная регрессия и корреляция
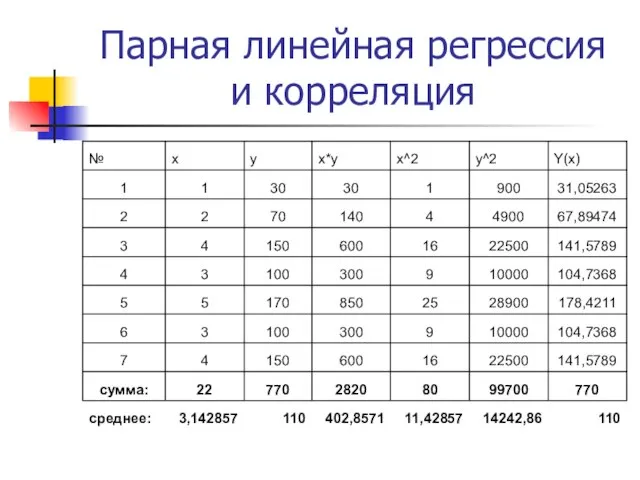
Слайд 21Парная линейная регрессия и корреляция

Слайд 22Парная линейная регрессия и корреляция

Слайд 23Парная линейная регрессия и корреляция

Слайд 24Парная линейная регрессия и корреляция

Слайд 25Парная линейная регрессия и корреляция

Слайд 26Парная линейная регрессия и корреляция

Слайд 27Оценка существенности параметров линейной регрессии и корреляции

Слайд 28Оценка существенности параметров линейной регрессии и корреляции

Слайд 29Оценка существенности параметров линейной регрессии и корреляции

Слайд 30Оценка существенности параметров линейной регрессии и корреляции

Слайд 31Оценка существенности параметров линейной регрессии и корреляции
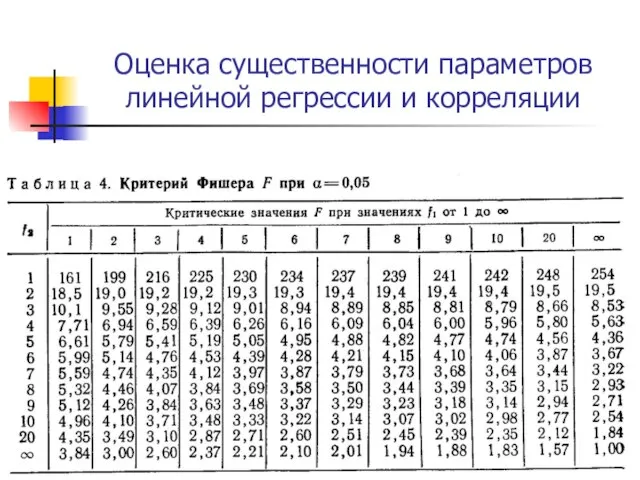
Слайд 32Оценка существенности параметров линейной регрессии и корреляции
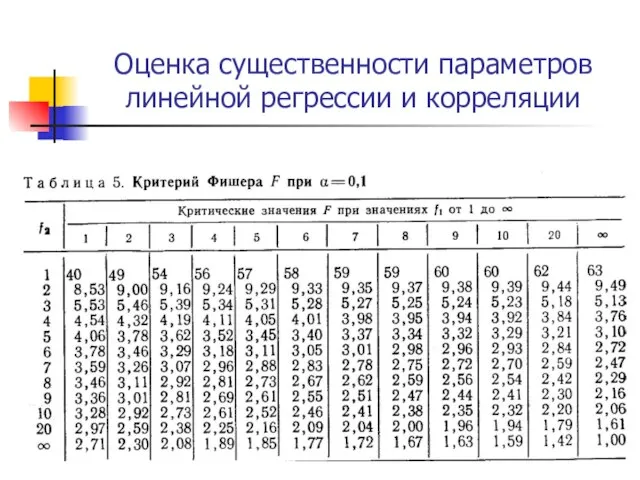
Слайд 33Оценка существенности параметров линейной регрессии и корреляции
































 Куб
Куб Площадь и объём фигуры
Площадь и объём фигуры Логарифмическая спираль
Логарифмическая спираль Проценты и десятичные дроби
Проценты и десятичные дроби Аналитическая геометрия. Уравнения прямой
Аналитическая геометрия. Уравнения прямой Правила вычисления производных
Правила вычисления производных Презентация на тему Арифметика Магницкого
Презентация на тему Арифметика Магницкого  Презентация на тему Площади многоугольников
Презентация на тему Площади многоугольников  Построение конуса с вырезом
Построение конуса с вырезом Функция. Предел функции. (часть 1)
Функция. Предел функции. (часть 1) Презентация на тему Формирование УУД на уроках математики в 5 классе
Презентация на тему Формирование УУД на уроках математики в 5 классе  Упрощение выражений (5 лкасс)
Упрощение выражений (5 лкасс) Решение логических задач
Решение логических задач Уравнения и неравенства с параметрами. 11 класс
Уравнения и неравенства с параметрами. 11 класс Функция. Свойства функций. Урок №1
Функция. Свойства функций. Урок №1 Десятки. Мозаика заданий
Десятки. Мозаика заданий Многогранник
Многогранник Презентация на тему Разложение многочлена на множители 7 класс
Презентация на тему Разложение многочлена на множители 7 класс  Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах
Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах Различные способы доказательств в курсе геометрии
Различные способы доказательств в курсе геометрии Две задачи на дроби
Две задачи на дроби Треугольник
Треугольник Нахождение угла треугольника
Нахождение угла треугольника Презентация на тему Тригонометрия
Презентация на тему Тригонометрия  Презентация на тему Умножение десятичных дробей (5 класс)
Презентация на тему Умножение десятичных дробей (5 класс)  Взаимное расположение графиков линейных функций. 7 класс
Взаимное расположение графиков линейных функций. 7 класс Парная линейная регрессия
Парная линейная регрессия Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ
Презентация на тему ШАРАДЫ, МЕТАГРАММЫ, ЛОГОГРИФЫ