- Главная
- Математика
- Икосаэдр

Содержание
- 2. Происхождение названия Названия многих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра»
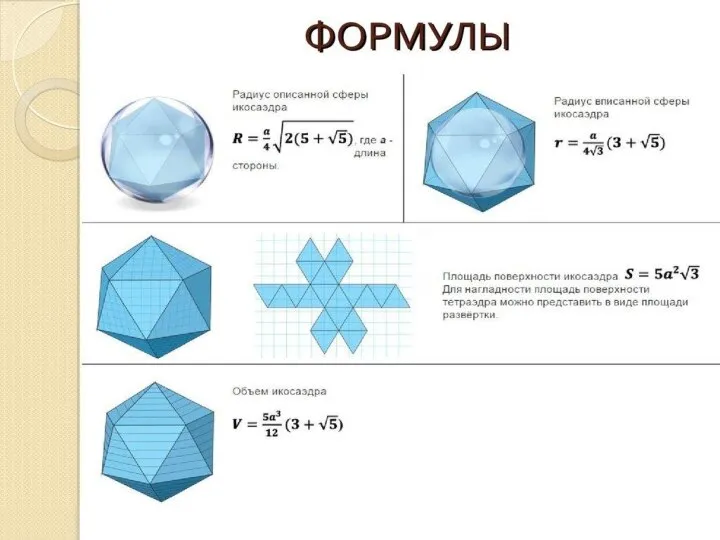
- 3. Характеристика икосаэдра Тип грани – правильный треугольник; Число сторон у грани – 3; Общее число граней
- 4. Свойства икосаэдра Каждая из 12 вершин икосаэдра лежит по 3 в 4-х параллельных плоскостях, образуя во
- 6. Усечённый икосаэдр.
- 7. Усечённый икосаэдр в жизни
- 11. Скачать презентацию
Слайд 2Происхождение названия
Названия многих многогранников пришли из Древней Греции, и в них указывается
Происхождение названия
Названия многих многогранников пришли из Древней Греции, и в них указывается

число граней:
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Отсюда название ИКОСАЭДР
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Отсюда название ИКОСАЭДР
Слайд 3Характеристика икосаэдра
Тип грани – правильный треугольник;
Число сторон у грани
Характеристика икосаэдра
Тип грани – правильный треугольник;
Число сторон у грани

– 3;
Общее число граней – 20;
Число рёбер примыкающих к вершине – 5;
Общее число вершин – 12;
Общее число рёбер – 30;
Общее число граней – 20;
Число рёбер примыкающих к вершине – 5;
Общее число вершин – 12;
Общее число рёбер – 30;
Слайд 4Свойства икосаэдра
Каждая из 12 вершин икосаэдра лежит по 3 в 4-х
Свойства икосаэдра
Каждая из 12 вершин икосаэдра лежит по 3 в 4-х

параллельных плоскостях, образуя во всех плоскостях правильный треугольник.
10 вершин икосаэдра находятся в 2-х параллельных плоскостях, и образуют в них 2 правильных 5-ти угольника
В икосаэдр можно вписать тетраэдр, таким образом, чтобы 4 вершины тетраэдра станут совмещены с 4-мя вершинами икосаэдра.
Икосаэдр возможно вписать в додекаэдр, тогда вершины икосаэдра совместятся с центрами граней додекаэдра.
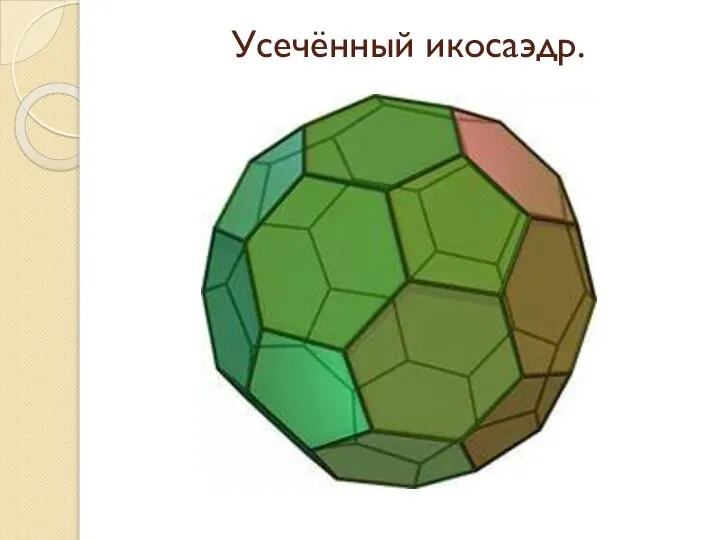
Усечённый икосаэдр можно получить, срезав 12 вершин с образованием граней вида правильных5-ти угольников. Тогда количество вершин нового многогранника увеличится в 5 раз (12×5=60), 20 треугольных граней становятся правильными шестиугольниками (количество граней теперь 20+12=32), а рёбер - 30+12×5=90.
Сделать икосаэдра можно из 20 тетраэдров.
10 вершин икосаэдра находятся в 2-х параллельных плоскостях, и образуют в них 2 правильных 5-ти угольника
В икосаэдр можно вписать тетраэдр, таким образом, чтобы 4 вершины тетраэдра станут совмещены с 4-мя вершинами икосаэдра.
Икосаэдр возможно вписать в додекаэдр, тогда вершины икосаэдра совместятся с центрами граней додекаэдра.
Усечённый икосаэдр можно получить, срезав 12 вершин с образованием граней вида правильных5-ти угольников. Тогда количество вершин нового многогранника увеличится в 5 раз (12×5=60), 20 треугольных граней становятся правильными шестиугольниками (количество граней теперь 20+12=32), а рёбер - 30+12×5=90.
Сделать икосаэдра можно из 20 тетраэдров.
Слайд 6Усечённый икосаэдр.
Усечённый икосаэдр.
Слайд 7Усечённый икосаэдр в жизни
Усечённый икосаэдр в жизни



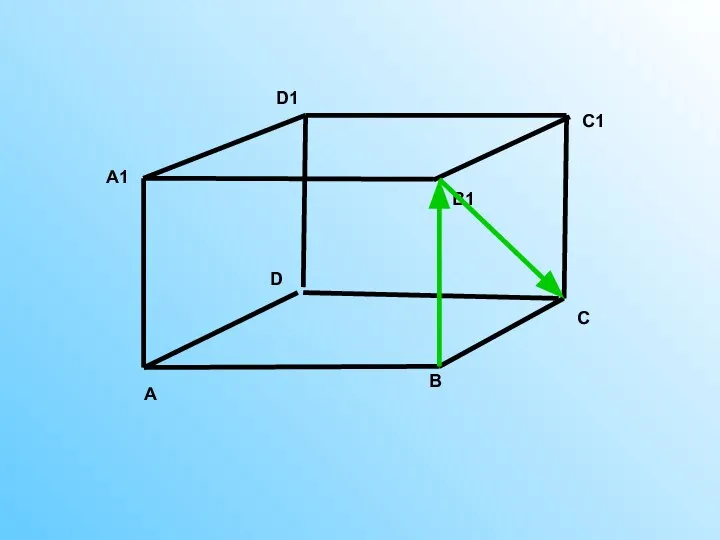 Угол между векторами
Угол между векторами Решение текстовых задач с помощью систем линейных уравнений
Решение текстовых задач с помощью систем линейных уравнений Свойства умножения
Свойства умножения Признаки равенства треугольников. Подготовка к контрольной работе
Признаки равенства треугольников. Подготовка к контрольной работе Практико-ориентированные задачи по математике про шины
Практико-ориентированные задачи по математике про шины Рисование старинного терема из геометрических форм
Рисование старинного терема из геометрических форм Направления геймификации современного образовательного процесса на уроках математики и информатики и во внеурочной деятельности
Направления геймификации современного образовательного процесса на уроках математики и информатики и во внеурочной деятельности Арифметическая прогрессия
Арифметическая прогрессия Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс Приемы вычислений для случаев вида 27+7
Приемы вычислений для случаев вида 27+7 Математический словарь
Математический словарь Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямых и плоскостей
Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямых и плоскостей Определитель матрицы. Правило Крамера
Определитель матрицы. Правило Крамера Длина отрезка
Длина отрезка Давай посчитаем. Свинки на тропинке
Давай посчитаем. Свинки на тропинке Вычислить интеграл
Вычислить интеграл Обыкновенные дифференциальные уравнения. (Лекция 5)
Обыкновенные дифференциальные уравнения. (Лекция 5) Решение задач. Параллельные прямые
Решение задач. Параллельные прямые Решение задач. Тест
Решение задач. Тест Этапы моделирования
Этапы моделирования Задачи на дроби. Урок 116
Задачи на дроби. Урок 116 Смежные и вертикальные углы
Смежные и вертикальные углы Площадь прямоугольника. Урок-открытие. 2 класс
Площадь прямоугольника. Урок-открытие. 2 класс Скалярное произведение векторов
Скалярное произведение векторов Своя игра 2
Своя игра 2 Показатели вариации
Показатели вариации Первообразная
Первообразная Скалярное произведение векторов
Скалярное произведение векторов