Слайд 2Пусть D(x, y) - некоторое множество точек плоскости Oxy. Если каждой упорядоченной

паре чисел (x, y) из области D соответствует определенное число z ∈ Z ⊂ R, то говорят, что z есть функция двух независимых переменных x и y .
Слайд 3Переменные x и y называются независимыми переменными, или аргументами, D - областью

определения, или существования, функции, а множество Z всех значений функции - областью ее значений. Функциональную зависимость z от x и y записывают в виде z = f(x, y), z = z(x, y),
Слайд 4Аналогично определяется функция n независимых переменных
z = f(x1, x2,..., xn).
Областью определения такой

функции будет множество D ⊂ Rn. Примером функций многих переменных в экономике являются производственные функции. При рассмотрении любого производственного комплекса как открытой системы (входами которой служат затраты ресурсов - людских и материальных, а выходами - продукция) производственная функция выражает устойчивое количественное соотношение между входами и выходами.
Слайд 5Частной производной функции нескольких переменных по одной из этих переменных называется производная,

взятая по этой переменной при условии, что все остальные переменные остаются постоянными. Для функции двух переменных z = f(x, y) частной производной по переменной x называется производная этой функции по x при постоянном y.
Слайд 6Обозначается частная производная по x следующим образом:

Слайд 7Аналогично частной производной функции z = f(x, y) по аргументу y называется

производная этой функции по y при постоянном x. Обозначения:
Слайд 8Частными производными второго порядка функции z = f(x, y) называются частные производные

от ее частных производных первого порядка. Если первая производная была взята, например, по аргументу x, то вторые производные обозначаются символами
Слайд 9Функция многих переменных может иметь максимум или минимум (экстремум) только в точках,

лежащих внутри области определения функции, в которой все ее частные производные первого порядка равны нулю или не существует хотя бы одна из них. Такие точки называются критическими.
Слайд 10Достаточные условия экcтремума для функции двух переменных.
Пусть точка Mo(xo, yo) -

критическая точка функции z = f(x, y), т.е.
и функция z = f(x, y) имеет непрерывные вторые частные производные в некоторой окрестности точки Mo(xo, yo).
Слайд 11Обозначим
Тогда:
если Δ > 0, то функция z имеет экстремум в точке Mo:

максимум при A < 0, минимум при
A > 0;
2) если Δ < 0, то экстремума в точке Mo нет;
3) если Δ = 0, то требуется дополнительное исследование.











 Прогрессия
Прогрессия Дифференциальные уравнения. Лекция 3
Дифференциальные уравнения. Лекция 3 Метр. (2класс)
Метр. (2класс) Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Число и цифра 5. Дидактическое пособие для детей 4-5 лет
Число и цифра 5. Дидактическое пособие для детей 4-5 лет Симметрия и асимметрия
Симметрия и асимметрия Решение неопределенных интегралов
Решение неопределенных интегралов Занятие 01.10+Задания для п.р
Занятие 01.10+Задания для п.р Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим
Лабораторная работа №1. Вычисление прямоугольных координат по геодезическим Одночлен и его стандартный вид
Одночлен и его стандартный вид Числовая окружность. Занятие 1-2
Числовая окружность. Занятие 1-2 Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Тригонометрия. Учебно-игровое пособие
Тригонометрия. Учебно-игровое пособие Предел функции
Предел функции Скалярное произведение векторов. Решение задач
Скалярное произведение векторов. Решение задач Анализ данных. Описательные статистики
Анализ данных. Описательные статистики Понятие корня
Понятие корня Международный день головоломки
Международный день головоломки Собери съедобные грибы в корзинку
Собери съедобные грибы в корзинку Презентация на тему Упрощение выражений (5 класс)
Презентация на тему Упрощение выражений (5 класс)  Религия Байеса
Религия Байеса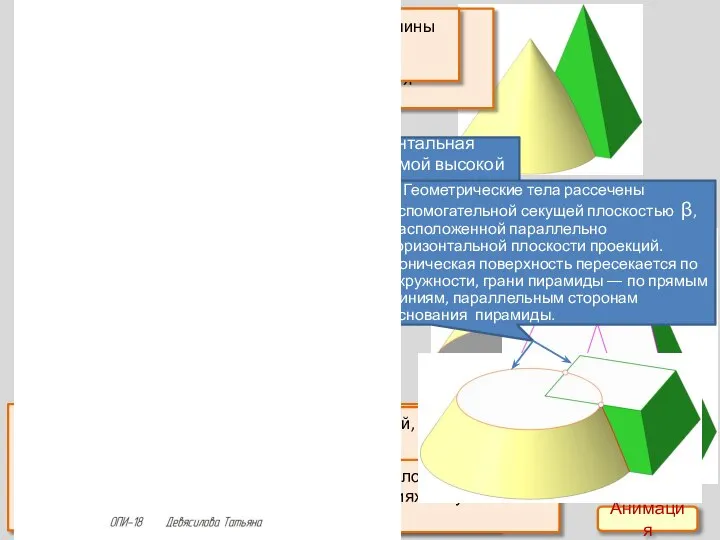 Пересечение поверхностей
Пересечение поверхностей Теория вероятностей
Теория вероятностей Учимся писать цифры
Учимся писать цифры Методика прикладных вычислений в конечных полях
Методика прикладных вычислений в конечных полях Свойства тригонометрических функций и их графики
Свойства тригонометрических функций и их графики Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля  Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА
Презентация на тему ЧЕТЫРЁХЗНАЧНЫЕ ЧИСЛА