Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ

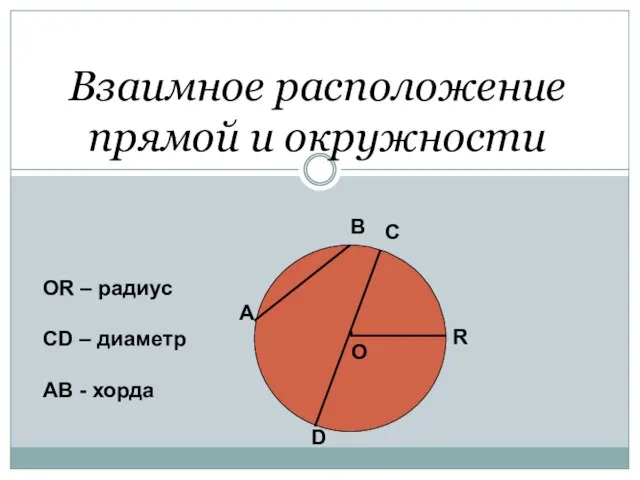
Взаимное расположение прямой и окружности
.
О
А
В
С
D
R
ОR – радиус
СD – диаметр
AB - хорда

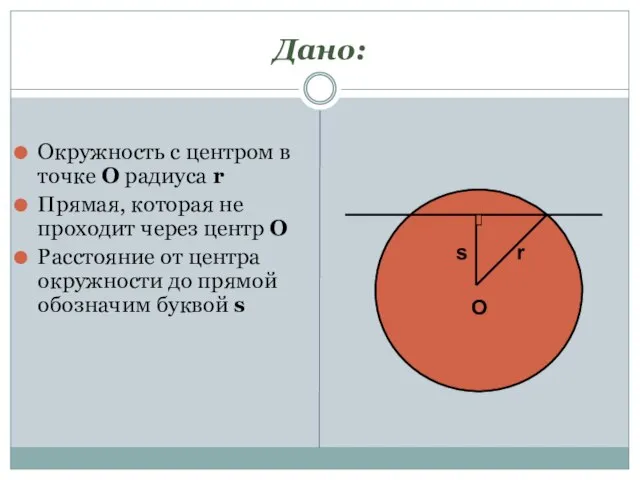
Дано:
Окружность с центром в точке О радиуса r
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой s
O
r
s

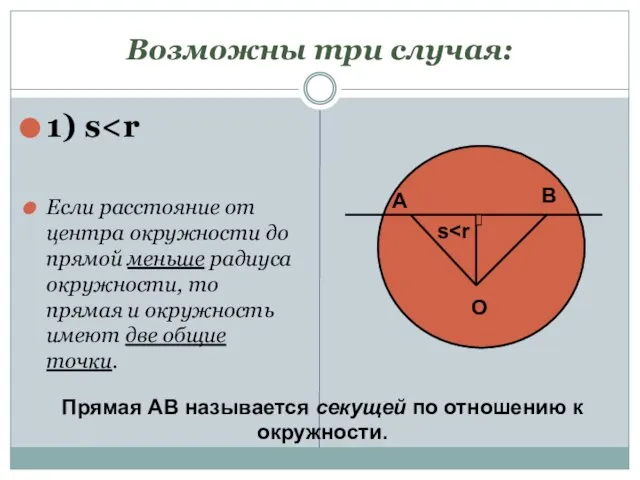
Возможны три случая:
1) s
Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
O
s
А
В
Прямая АВ называется секущей по отношению к окружности.

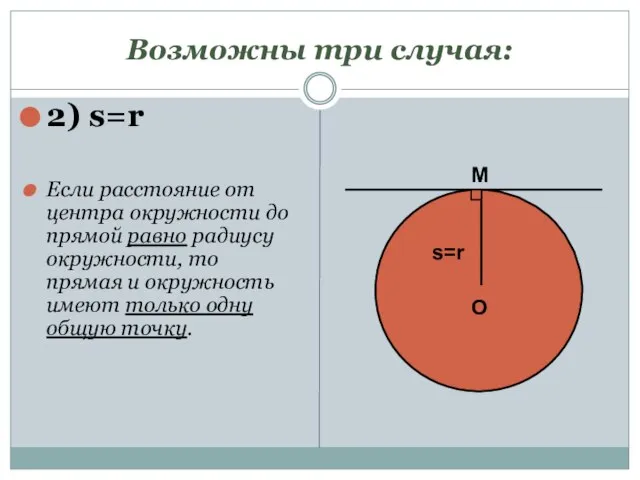
Возможны три случая:
2) s=r
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
O
s=r
M

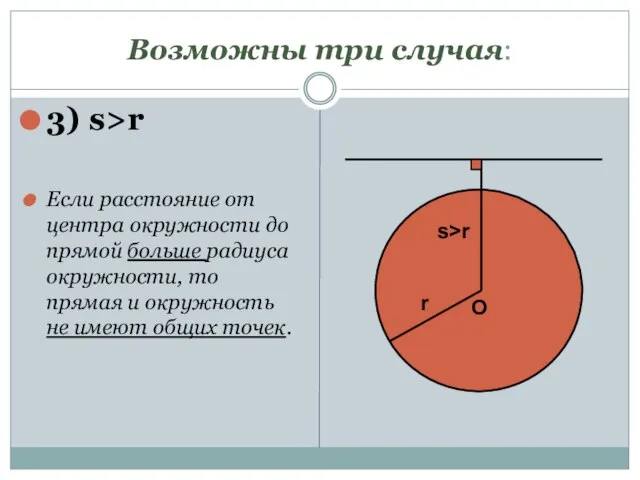
Возможны три случая:
3) s>r
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
O
s>r
r

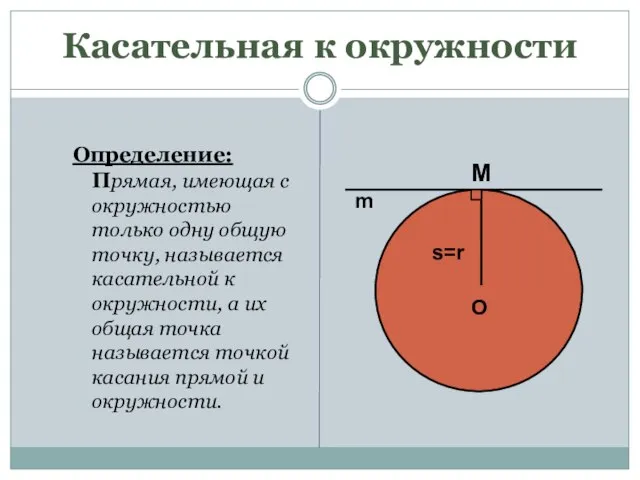
Касательная к окружности
Определение: Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
O
s=r
M
m

Выясните взаимное расположение прямой и окружности, если:
r = 15 см, s = 11см
r = 6 см, s = 5,2 см
r = 3,2 м, s = 4,7 м
r = 7 см, s = 0,5 дм
r = 4 см, s = 40 мм
прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая - касательная

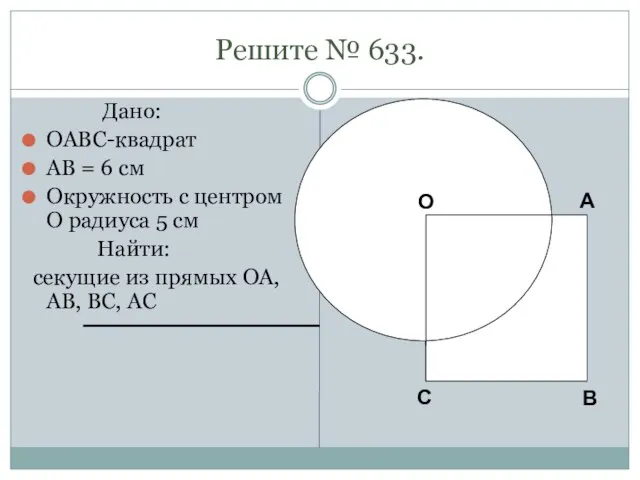
Решите № 633.
Дано:
OABC-квадрат
AB = 6 см
Окружность с центром O радиуса 5 см
Найти:
секущие из прямых OA, AB, BC, АС
О
А
В
С
О

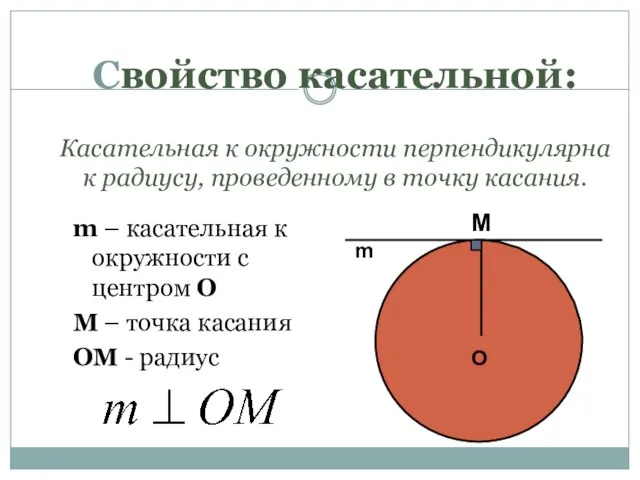
Свойство касательной:
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная к окружности с центром О
М – точка касания
OM - радиус
O
M
m

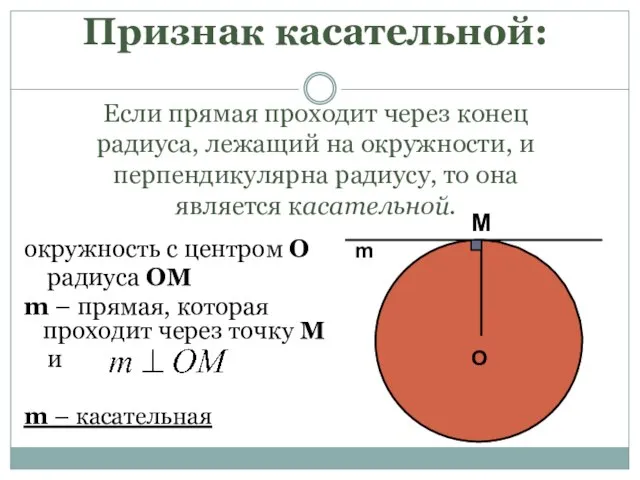
Признак касательной:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является касательной.
окружность с центром О
радиуса OM
m – прямая, которая проходит через точку М
и
m – касательная
O
M
m