Содержание
- 2. Примеры функций нескольких переменных S(a, b)=a·b – площадь прямоугольника со сторонами a и b. – период
- 3. Декартово произведение
- 4. Функция п действительных переменных Отображение f: Х →R, где называется действительной функцией п действительных переменных (аргументов).
- 5. Функции z=f(x; y) f: D →Z f: Х →R y=f(x1; x2;…; xn) Область определения (существования) функции
- 6. Окрестность точки δ-окрестностью точки М0 (х0; у0) называется множество всех точек М(х; у) плоскости хОу, координаты
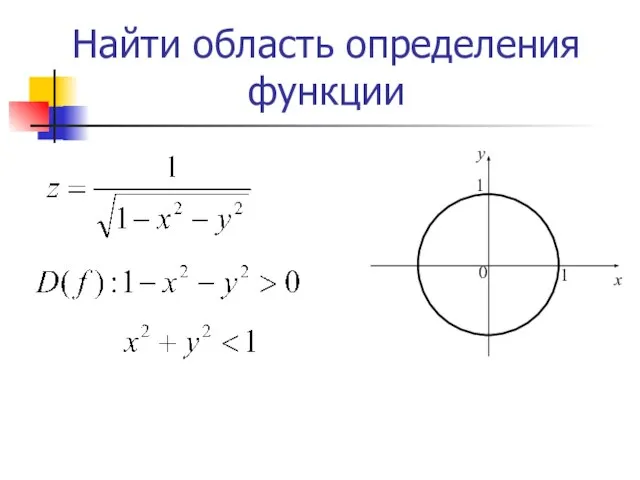
- 7. х y 0 Найти область определения функции 1 1
- 8. График функции f: Х→R При п=2 графиком функции является поверхность в R3.
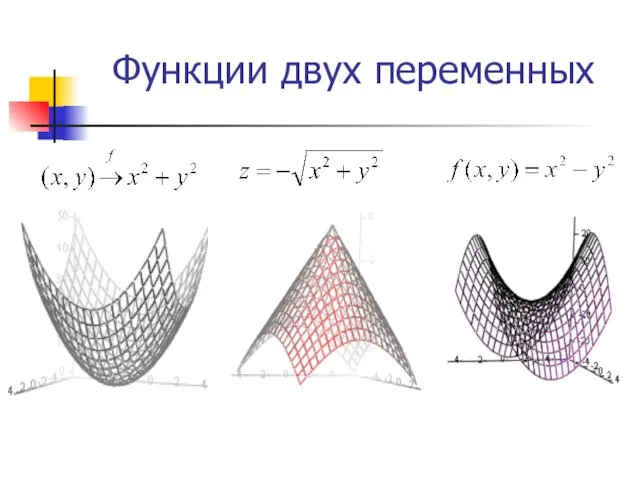
- 9. Функции двух переменных
- 10. Предел функции в точке М0 (х0; у0) (при х→х0 и у→у0)
- 11. Непрерывность функции в точке Функция z = f(x,y) называется непрерывной в точке М0 (х0; у0), если
- 12. Частные приращения функций двух переменных Функция z=f(x, y) определена в окрестности точки М(х, у). Δх –
- 13. Частные производные функции двух переменных Частной производной функции z=f(x, y) по переменной х называется предел, если
- 14. Частные производные функции двух переменных Частные производные функции z по переменным х и у. Обозначения частной
- 15. Геометрический смысл частных производных х у z z = f (x, y) 0 M0 Р у0
- 16. х у z z = f (x, y) 0 M у х Δх Δу y+Δy x+Δх
- 17. Дифференцируемость функции Функция z=f(x; y) называется дифференцируемой в точке М, если полное приращение этой функции можно
- 18. Полный дифференциал функции Полным дифференциалом дифференцируемой функции z=f(x; y) в точке М называется главная часть её
- 19. Необходимое условие дифференцируемости функции Если функция z=f(x; y) дифференцируема в точке М(х; у), то она непрерывна
- 20. Достаточное условие дифференцируемости функции Если функция z=f(x; y) в точке М(х; у) имеет непрерывные частные производные,
- 21. Частные производные высших порядков частные производные первого порядка (непрерывные и имеют частные производные) частные производные второго
- 22. Частные производные высших порядков частная производная третьего порядка
- 23. Теорема Шварца Если функция от п переменных определена в открытой п-мерной области, в которой существуют частные
- 24. Дифференциалы высших порядков полный дифференциал первого порядка дифференциал второго порядка z = f (x, y)
- 25. Точки экстремума Точка М0(х0, у0) области D называется точкой локального максимума (минимума) если существует В(М0, δ),
- 26. Необходимое условие существования экстремума Если функция z=f(x, y) определена и дифференцируема в В(М0, δ) и имеет
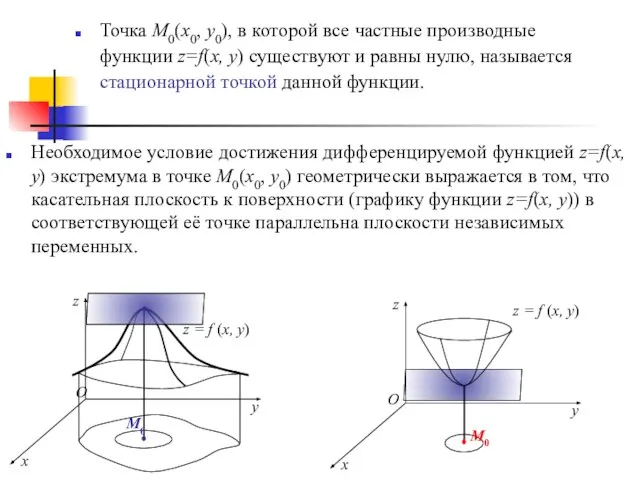
- 27. Необходимое условие достижения дифференцируемой функцией z=f(x, y) экстремума в точке М0(х0, у0) геометрически выражается в том,
- 28. Замечание. Функция z=f(x, y) может иметь экстремум и в таких точках, в которых по крайней мере
- 29. Достаточное условие существования экстремума Пусть функция z=f(x, y) определена, непрерывна и непрерывно дифференцируема до второго порядка
- 30. Замечание. Стационарная точка функции z=f(x, y) может и не являться точкой экстремума. Например, функция в точке
- 32. Скачать презентацию


























 Урок математики в 1 классе
Урок математики в 1 классе Буквенные выражения
Буквенные выражения Дискретное преобразование Фурье (окончание)
Дискретное преобразование Фурье (окончание) Третий признак подобия треугольников
Третий признак подобия треугольников Линейная регрессия
Линейная регрессия Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Сфера и плоскость
Сфера и плоскость Уравнение. Корень уравнения
Уравнение. Корень уравнения Степень с натуральным показателем и ее свойства. Обобщение. 7 класс
Степень с натуральным показателем и ее свойства. Обобщение. 7 класс Противоположные числа. Устный счет
Противоположные числа. Устный счет Сумма и разность синусов, косинусов
Сумма и разность синусов, косинусов Теоремы синусов и косинусов. Тест
Теоремы синусов и косинусов. Тест Справочный материал. 9 класс
Справочный материал. 9 класс Элементы теории множеств. Математические основы информатики
Элементы теории множеств. Математические основы информатики Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы Письменное умножение на трёхзначное число
Письменное умножение на трёхзначное число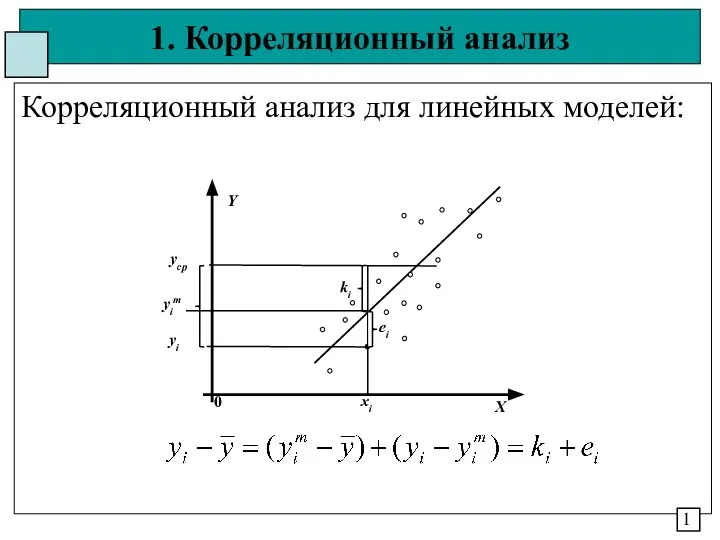 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Подготовка к ГИА по математике. Задания 6
Подготовка к ГИА по математике. Задания 6 Презентация на тему О числах
Презентация на тему О числах  Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Презентация на тему Числовые неравенства и их свойства
Презентация на тему Числовые неравенства и их свойства  Построение диаграмм и графиков
Построение диаграмм и графиков Тесты по математике
Тесты по математике Геометрическая прогрессия
Геометрическая прогрессия Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Сумма углов треугольника
Сумма углов треугольника Вычисление площадей плоских фигур с помощью определенного интеграла
Вычисление площадей плоских фигур с помощью определенного интеграла Линии на плоскости
Линии на плоскости