Слайд 2-Повелеваю, написать мне все о математике. Как она возникла, какой была раньше,

какой стала теперь, какой будет в будущем.
Слайд 4Задача 1.
Прямоугольный треугольник разбит на четыре геом. фигуры, как показано на рисунке.
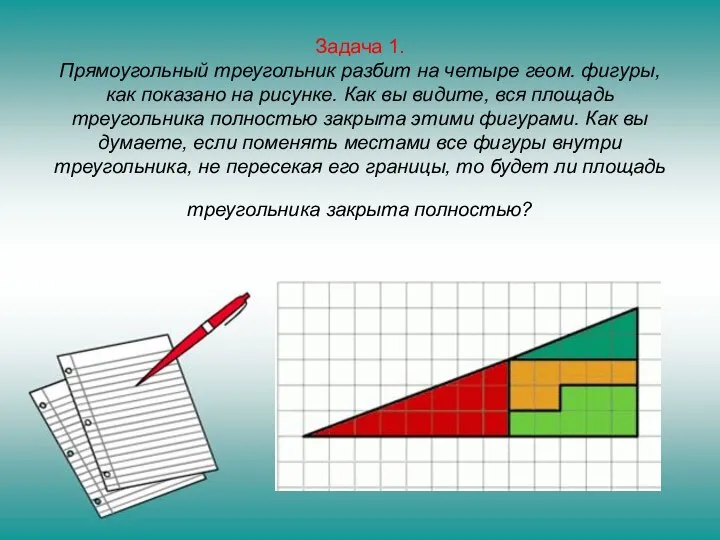
Как вы видите, вся площадь треугольника полностью закрыта этими фигурами. Как вы думаете, если поменять местами все фигуры внутри треугольника, не пересекая его границы, то будет ли площадь треугольника закрыта полностью?
Слайд 6 Это задание – пример математического парадокса.
Среди причин, способных возбуждать интерес

к математике, особую роль играют парадоксы. Парадоксы выделяются тем, что могут заинтересовать человека далекого от математики. В подобных задачах после увиденного возникает желание добраться до истины.
Слайд 7 Задача 2.
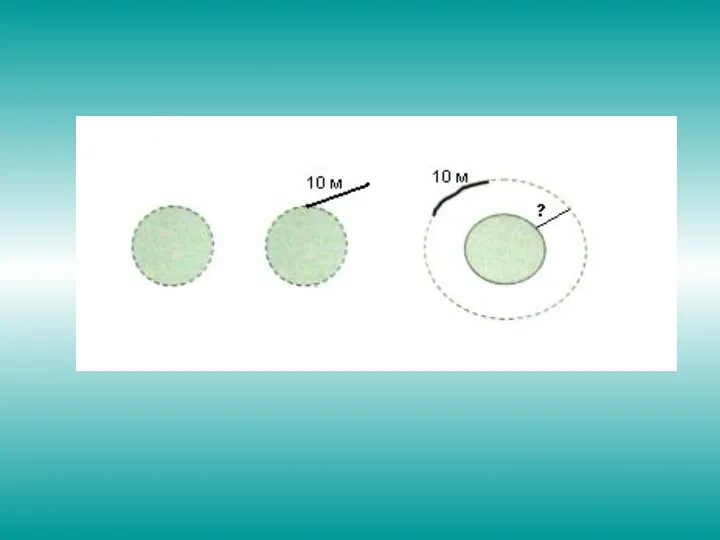
Представьте, что Землю опоясали веревкой по экватору. Осталось 10 лишних

метров. Тогда концы веревки соединили и расправили веревку так, чтобы с экватором получилась концентрическая окружность. Какой будет зазор между веревкой и Землей?
Слайд 9C = 2 π r C + 10 = 2 π (r

+ x)
C = 2 π r + 2 π x – 10
2 π r = 2 π r + 2 π x – 10
2 π x = 10
X = 10 : 2 π
X ≈ 1,59 м
Слайд 10 Такие задачи, демонстрируют несоответствие интуитивных ожиданий реальному положению дел. Когда вдруг

выясняется, что здравый смысл без вычислений не всегда может делать правильные выводы, возникают соображения типа «не пора ли выучить математические формулы». Нельзя не согласиться с Аристотелем «Познание начинается с удивления».
Слайд 122 2 = ?
4 : 4 = 5 : 5
4(1 : 1)
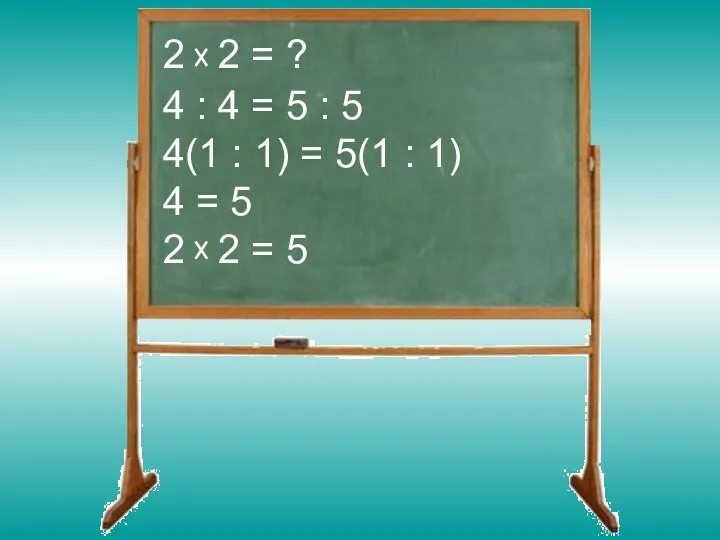
= 5(1 : 1)
4 = 5
2 2 = 5
Слайд 13 Софизмом называется умышленно ложное умозаключение, которое имеет видимость правильного. Любой софизм

содержит одну или несколько замаскированных ошибок. Разбор софизмов прежде всего развивает логическое мышление. Обнаружить ошибку в софизме это значит осознать ее, а осознание ошибки предупреждает повторение ее в дальнейшем в других математических рассуждениях. Разбор софизмов помогает сознательному усвоению изучаемого математического материала, развивает наблюдательность, вдумчивость и критическое отношение к тому, что изучается. Математические софизмы заставляют тщательно следить за точностью формулировок, правильностью записей и чертежей, что особенно важно при подготовке к ГИА.
Слайд 14Виды четырёхугольников
Прямоугольник
Квадрат
Ромб
Трапеция
Параллелограмм
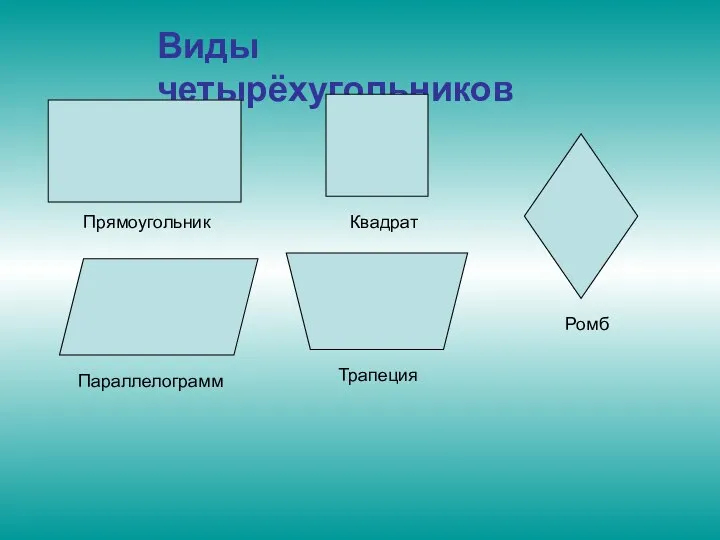
Слайд 15- Давайте отправимся все в царство четырехугольников. Кто первый придет, тот и

будет королем
Слайд 16- Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения

делятся пополам
Слайд 17Прямоугольник
Квадрат
Ромб
Трапеция
Параллелограмм
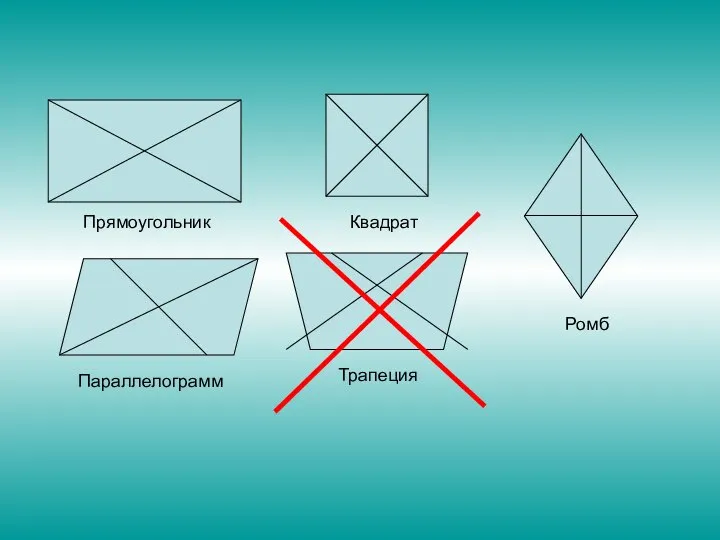
Слайд 18- Пройдут только те, у кого диагонали равны

Слайд 19Прямоугольник
Квадрат
Ромб
Параллелограмм
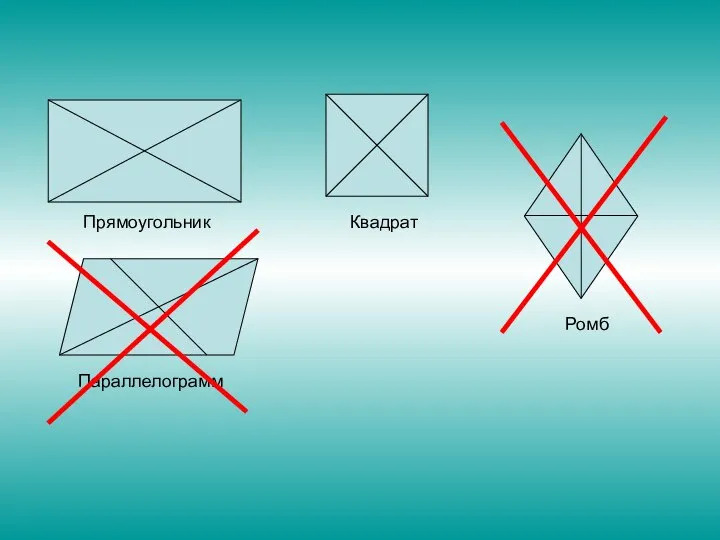
Слайд 20- Пропущу только тех, у кого диагонали пересекаются под прямым углом

Слайд 23 В данной ролевой игре использовался метод исключения, который эффективен при работе

с тестовым материалом.









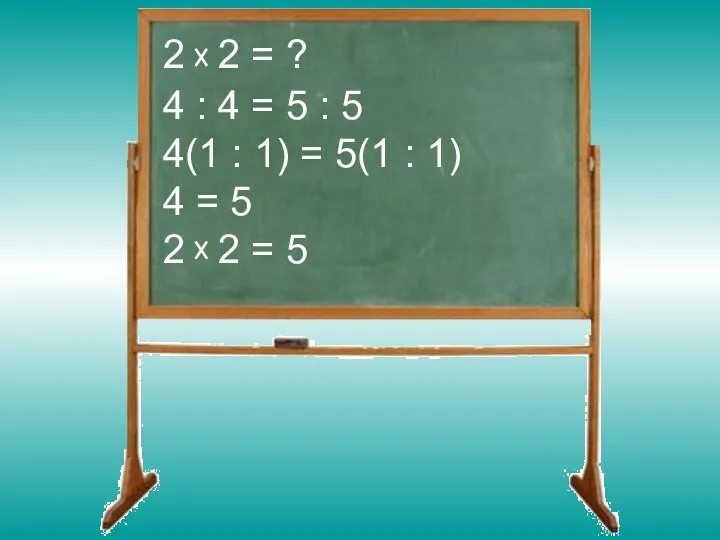












 Численное интегрирование
Численное интегрирование Десятичные дроби. Уравнения
Десятичные дроби. Уравнения Презентация по математике "Величины. Длина" -
Презентация по математике "Величины. Длина" -  Стереометрия. Тренажер
Стереометрия. Тренажер Решение задач на смеси и сплавы. Основное вещество
Решение задач на смеси и сплавы. Основное вещество Перпендикулярність площин
Перпендикулярність площин Верные и неверные неравенства
Верные и неверные неравенства Умножение вектора на число
Умножение вектора на число Элементы статистики. Количество звонков в день за ноябрь
Элементы статистики. Количество звонков в день за ноябрь Геометрические фигуры: круг, квадрат, треугольник
Геометрические фигуры: круг, квадрат, треугольник Презентация на тему Счет от одного до десяти
Презентация на тему Счет от одного до десяти  Алгебра в жизни человека
Алгебра в жизни человека 11097_user_file_57e19
11097_user_file_57e19 Выборочное наблюдение
Выборочное наблюдение Векторы. Задачи
Векторы. Задачи Увлекательный мир умножения
Увлекательный мир умножения Перпендикулярные прямые
Перпендикулярные прямые Презентация на тему ГИА 2013. Модуль «Алгебра» №1
Презентация на тему ГИА 2013. Модуль «Алгебра» №1  Схема Бернулли. Формула полной вероятности. Формула Байеса
Схема Бернулли. Формула полной вероятности. Формула Байеса Понятие вектора в пространстве
Понятие вектора в пространстве Перпендикулярность плоскостей
Перпендикулярность плоскостей Таблица классов и разрядов. Свойства сложения
Таблица классов и разрядов. Свойства сложения Решение неравенств. 8 класс
Решение неравенств. 8 класс Многогранники. Решение задач
Многогранники. Решение задач Treasure and numbers
Treasure and numbers Презентация на тему Путешествие в страну Занимательной математики (1 класс)
Презентация на тему Путешествие в страну Занимательной математики (1 класс)  Расположение прямой и окружности
Расположение прямой и окружности Решение задач Параллельные прямые
Решение задач Параллельные прямые