Функция. Свойства функции

Cодержание
4
Определение функции.
1
2
5
Способы задания функции.
График функции.
Алгоритм описания свойств функции.
Свойства функции.
3
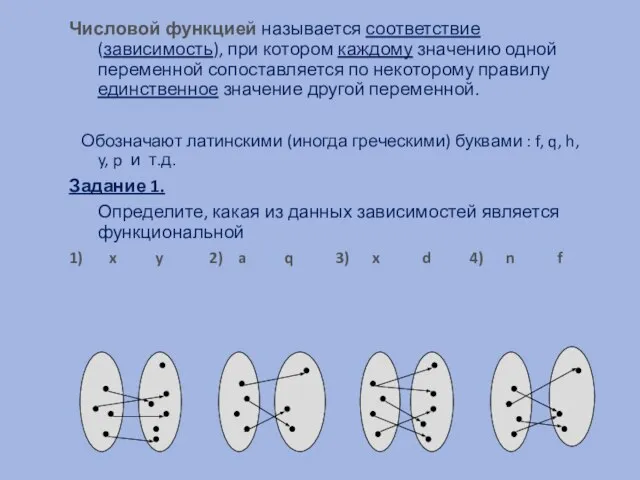
3

Числовой функцией называется соответствие (зависимость), при котором каждому значению одной переменной сопоставляется по некоторому правилу единственное значение другой переменной.
Обозначают латинскими (иногда греческими) буквами : f, q, h, y, p и т.д.
Задание 1.
Определите, какая из данных зависимостей является функциональной
1) x y 2) a q 3) x d 4) n f

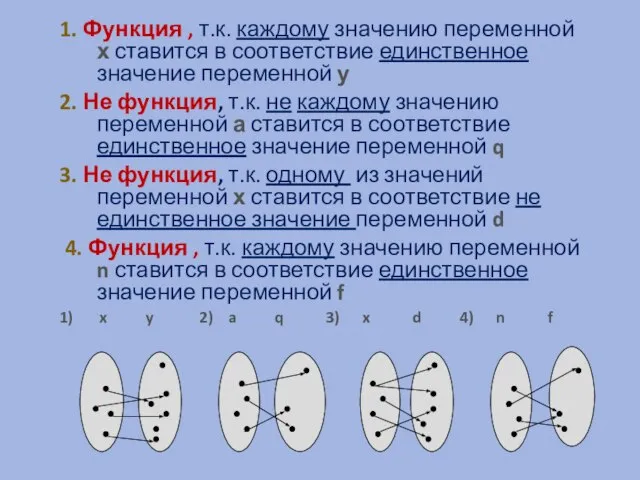
1. Функция , т.к. каждому значению переменной х ставится в соответствие единственное значение переменной у
2. Не функция, т.к. не каждому значению переменной а ставится в соответствие единственное значение переменной q
3. Не функция, т.к. одному из значений переменной х ставится в соответствие не единственное значение переменной d
4. Функция , т.к. каждому значению переменной n ставится в соответствие единственное значение переменной f
1) x y 2) a q 3) x d 4) n f

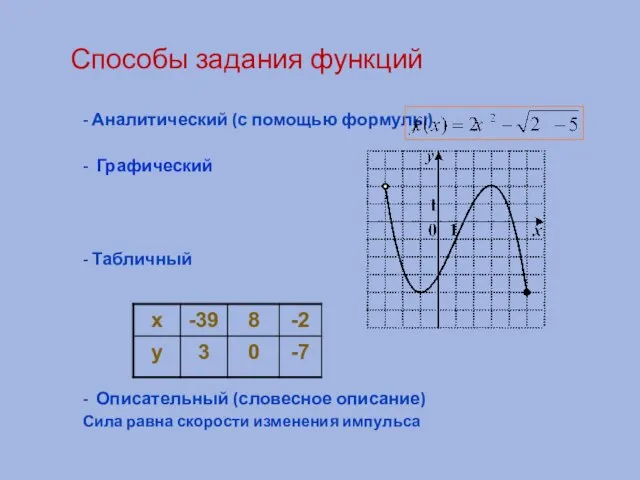
Способы задания функций
- Аналитический (с помощью формулы)
- Графический
- Табличный
- Описательный (словесное описание)
Сила равна скорости изменения импульса

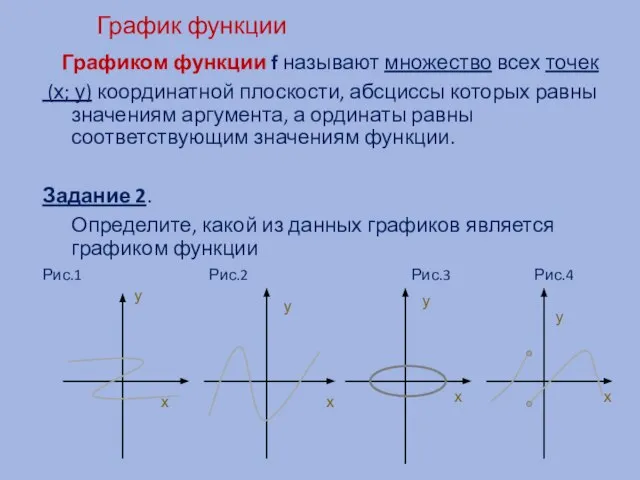
График функции
Графиком функции f называют множество всех точек
(х; у) координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты равны соответствующим значениям функции.
Задание 2.
Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
у
у
у
у
х
х
х
х

1. Область определения
2. Область значений
3. Нули функции
4. Четность
5. Промежутки знакопостоянства
6. Непрерывность
7. Монотонность
8. Наибольшее и наименьшее значения
9. Ограниченность
10. Выпуклость
СВОЙСТВА ФУНКЦИИ
Алгоритм описания свойств функции

1.Область определения
Область определения функции – все значения, которые принимает независимая переменная.
Обозначается : D (f).
Пример. Функция задана формулой у =
Данная формула имеет смысл при всех значениях
х ≠ -3, х ≠ 3,
поэтому D( y )=(- ∞;-3) U (-3;3) U (3; +∞)

2. Область значений
Область (множество) значений функции – все значения, которые принимает зависимая переменная.
Обозначается : E (f)
Пример. Функция задана формулой у =
Данная функция является квадратичной , график – парабола, вершина (0; 9)
поэтому E( y )= [ 9 ; +∞)

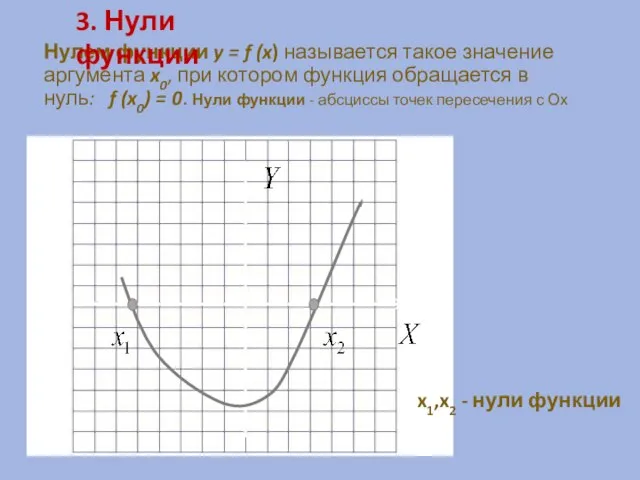
Нулем функции y = f (x) называется такое значение аргумента x0, при котором функция обращается в нуль: f (x0) = 0. Нули функции - абсциссы точек пересечения с Ох
3. Нули функции
x1,x2 - нули функции

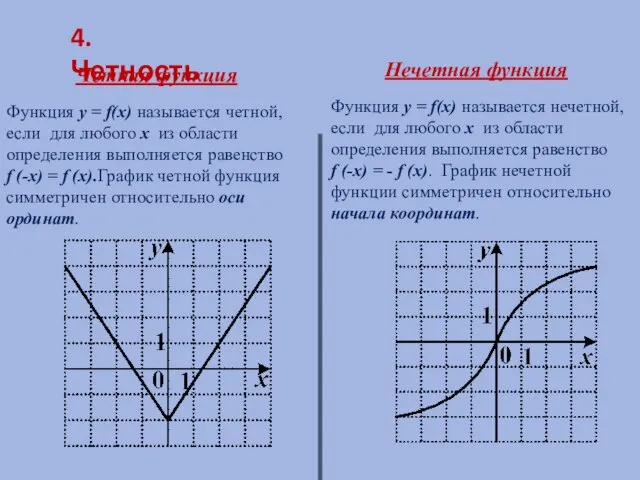
4. Четность
Четная функция
Нечетная функция
Функция y = f(x) называется четной, если для любого х из области определения выполняется равенство f (-x) = f (x).График четной функция симметричен относительно оси ординат.
Функция y = f(x) называется нечетной, если для любого х из области определения выполняется равенство
f (-x) = - f (x). График нечетной функции симметричен относительно начала координат.

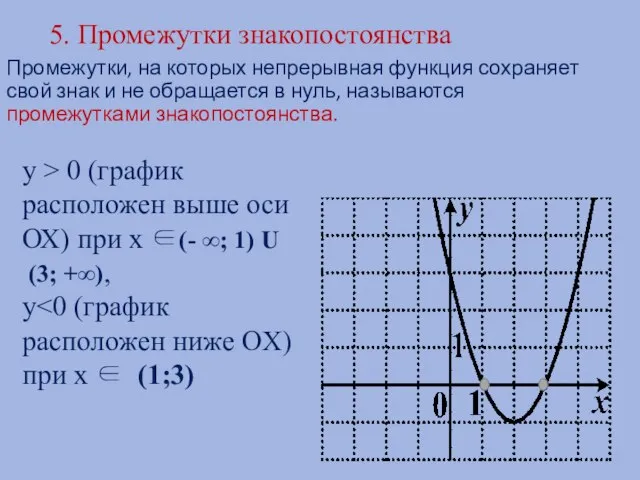
5. Промежутки знакопостоянства
Промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства.
y > 0 (график расположен выше оси ОХ) при х ∈(- ∞; 1) U
(3; +∞),
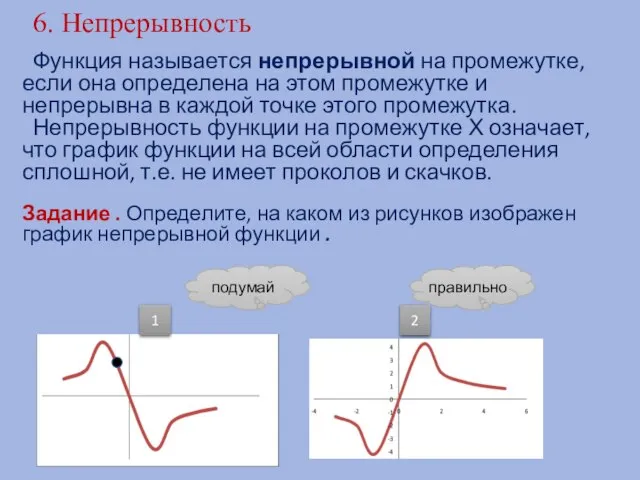
y<0 (график расположен ниже OX) при х ∈ (1;3)

6. Непрерывность
Функция называется непрерывной на промежутке, если она определена на этом промежутке и непрерывна в каждой точке этого промежутка.
Непрерывность функции на промежутке Х означает, что график функции на всей области определения сплошной, т.е. не имеет проколов и скачков.
Задание . Определите, на каком из рисунков изображен график непрерывной функции .
1
2
подумай
правильно

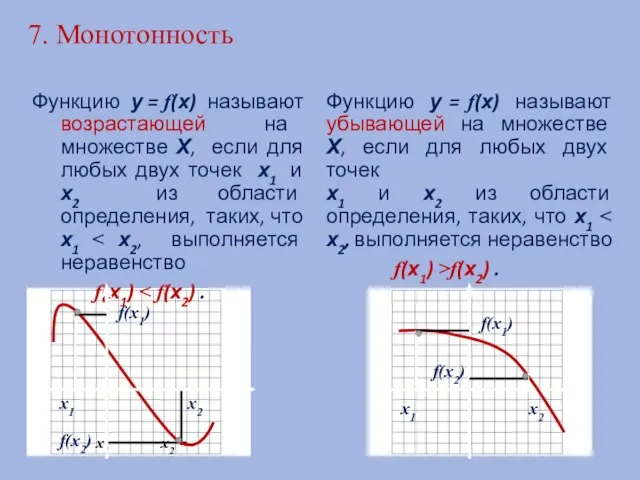
7. Монотонность
Функцию у = f(х) называют возрастающей на множестве Х, если для любых двух точек х1 и х2 из области определения, таких, что х1 < х2, выполняется неравенство
f(х1) < f(х2) .
Функцию у = f(х) называют убывающей на множестве Х, если для любых двух точек
х1 и х2 из области определения, таких, что х1 < х2, выполняется неравенство
f(х1) >f(х2) .
x1
х1
x2
f(x2)
f(x1)
x2
x1
x2
f(x2)
f(x1)

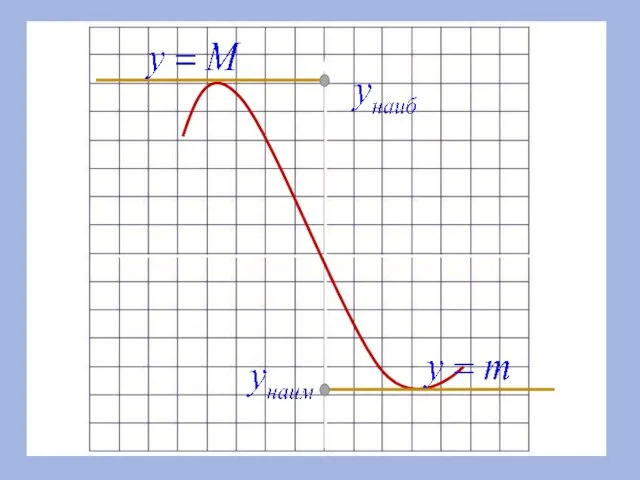
8.Наибольшее и наименьшее значения
Число m называют наименьшим значением функции
у = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что f(х0) = m.
2) всех х из области определения выполняется неравенство
f(х) ≥ f(х0).
Число M называют наибольшим значением функции
у = f(х) на множестве Х, если:
1) в области определения существует такая точка х0, что f(х0) = M.
2) для всех х из области определения выполняется неравенство
f(х) ≤ f(х0).

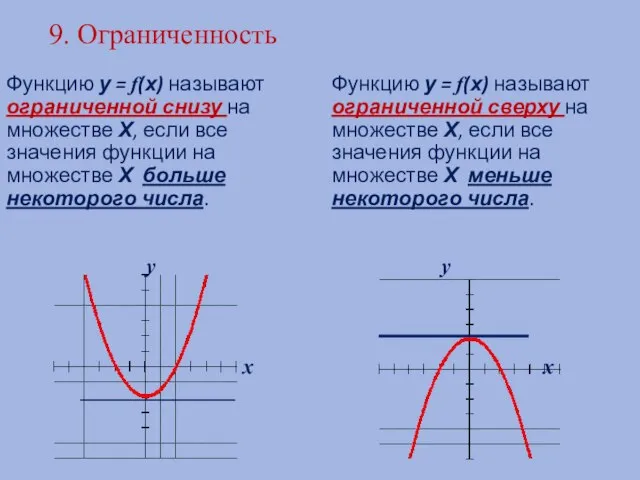
9. Ограниченность
Функцию у = f(х) называют ограниченной снизу на множестве Х, если все значения функции на множестве Х больше некоторого числа.
Функцию у = f(х) называют ограниченной сверху на множестве Х, если все значения функции на множестве Х меньше некоторого числа.
х
у
х
у

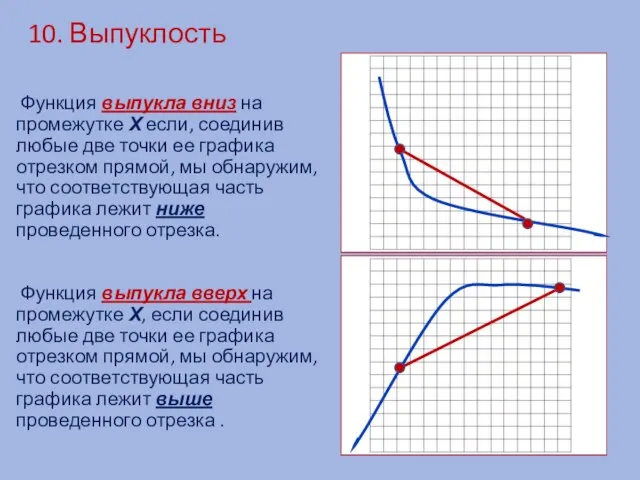
10. Выпуклость
Функция выпукла вниз на промежутке Х если, соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх на промежутке Х, если соединив любые две точки ее графика отрезком прямой, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка .