Однородные системы линейных алгебраических уравнений

О п р е д е л е н и е 1. Однородной системой линейных алгебраических уравнений (СЛАУ), состоящей из m уравнений с n неизвестными х1,…,хn, называется система вида:

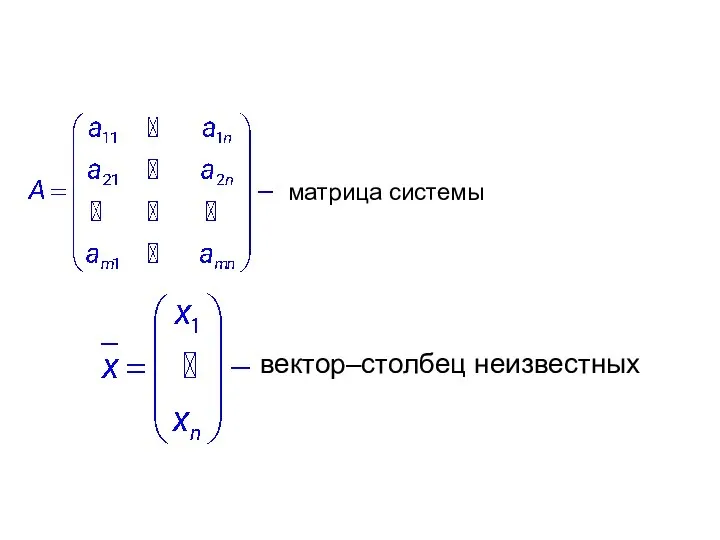
матрица системы
вектор–столбец неизвестных

Система линейных однородных уравнений всегда совместна, т. к. она всегда имеет, по крайней мере, нулевое решение .
Если в системе, а ее определитель отличен от нуля, то такая система имеет только нулевое решение, b=0.

Теорема1: Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг ее матрицы меньше количества неизвестных, .
В этом случае система имеет свободных
неизвестных, которые обозначают .

Однородная система линейных алгебраических уравнений Фундаментальная система решений
Обозначим решение системы
виде строки .
Теорема 2: Если - решение системы, то
- также решение этой системы.
Теорема 3: Если и -
решения системы (1), то при любых
линейная комбинация - также решение
данной системы.

Фундаментальная система решений (ФСР)
Определение . Система линейно независимых
решений называется фундаментальной,
если каждое решение системы (1) является линейной
комбинацией решений .
Теорема 4: Если ранг матрицы А r меньше числа
переменных n, то всякая фундаментальная система
решений системы (1) состоит из решений.

Фундаментальная система решений
Пример. Найти общее решение и ФСР однородной системы
Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

Ранг матрицы равен 2, свободные неизвестные,