Содержание
- 2. Линейная функция y = kx + b
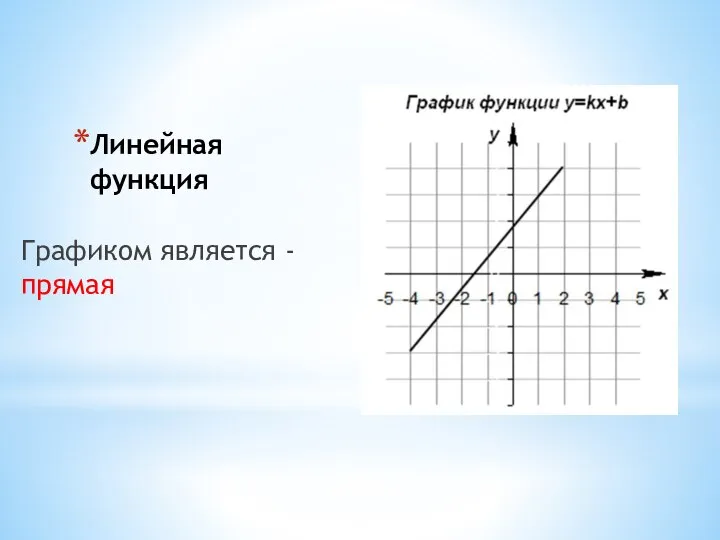
- 3. Линейная функция Графиком является - прямая
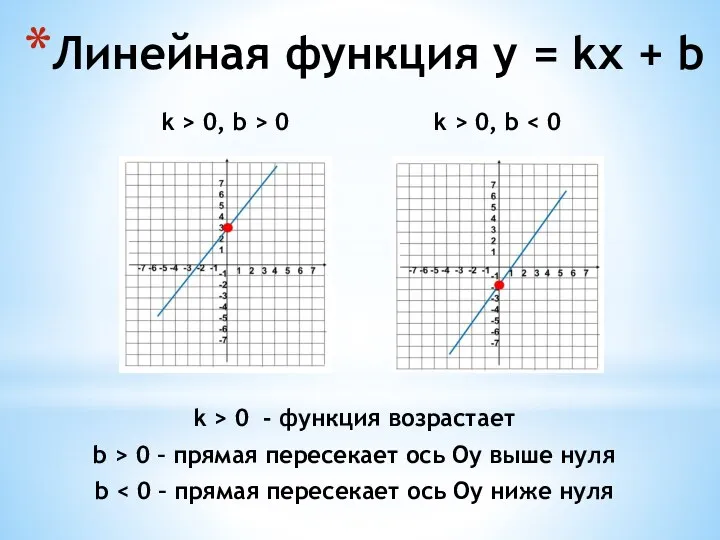
- 4. k > 0, b > 0 k > 0, b Линейная функция y = kx +
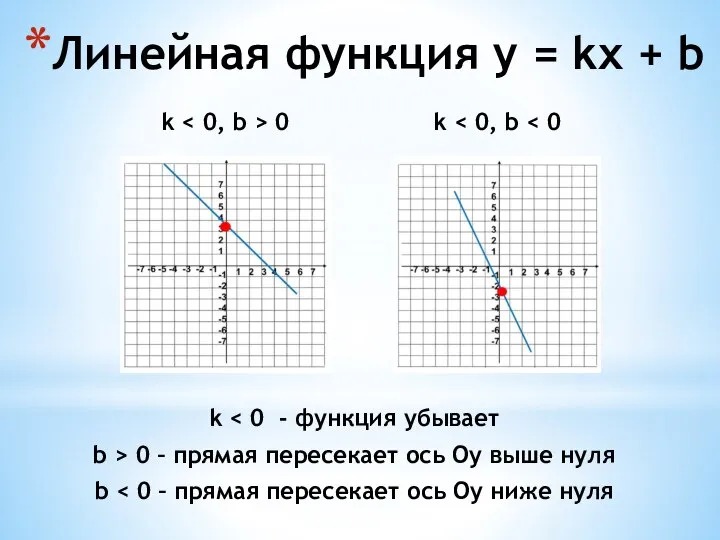
- 5. k 0 k Линейная функция y = kx + b k b > 0 – прямая
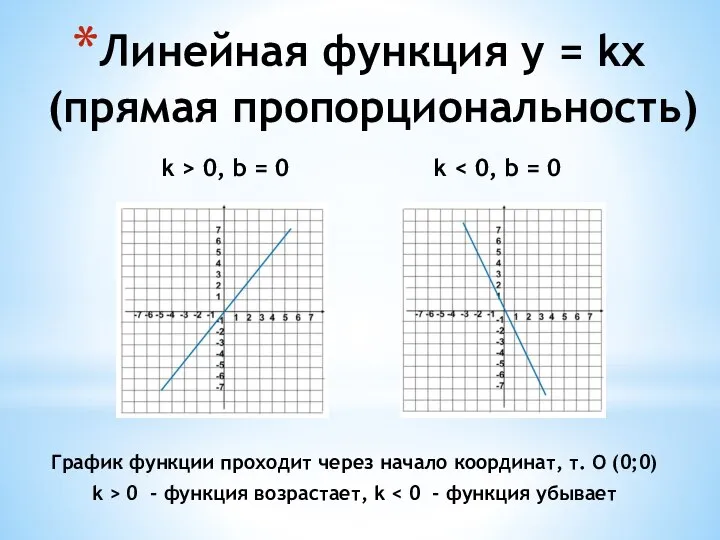
- 6. k > 0, b = 0 k Линейная функция y = kx (прямая пропорциональность) График функции
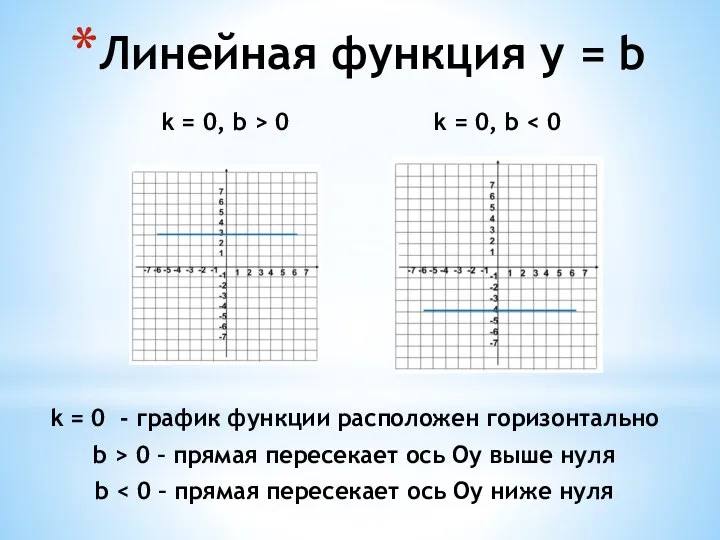
- 7. k = 0, b > 0 k = 0, b Линейная функция y = b k
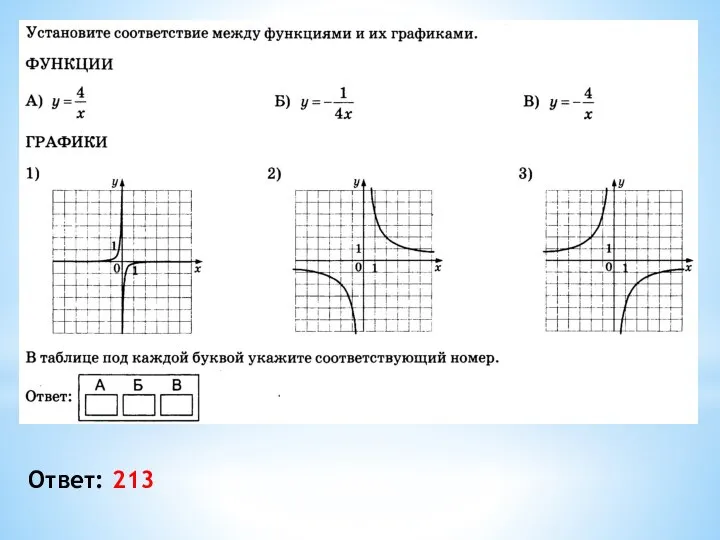
- 8. Ответ: 231
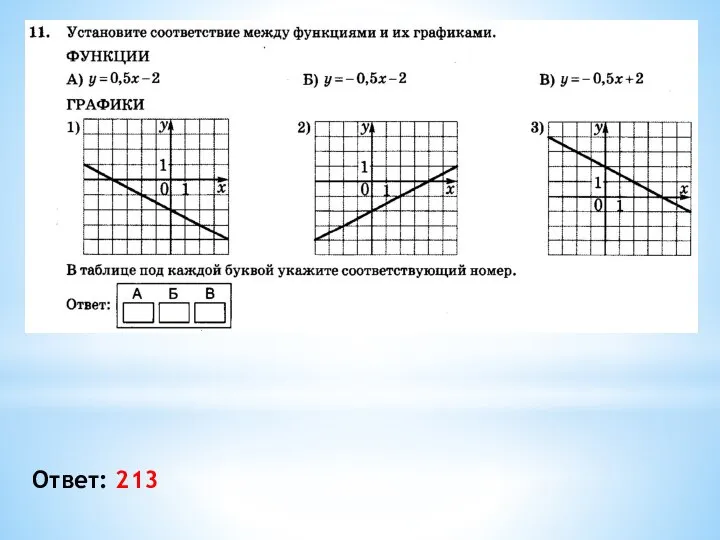
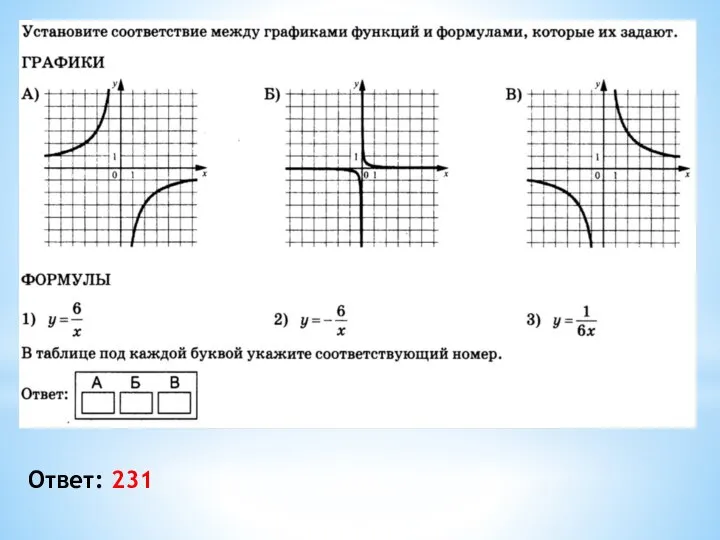
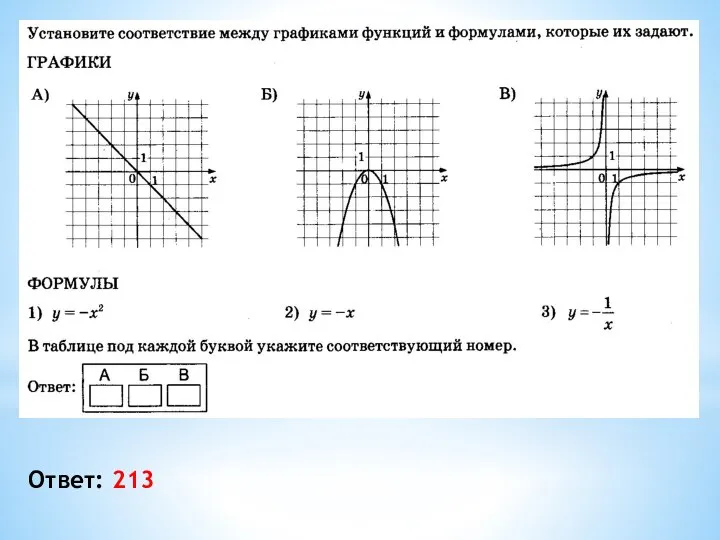
- 9. Ответ: 213
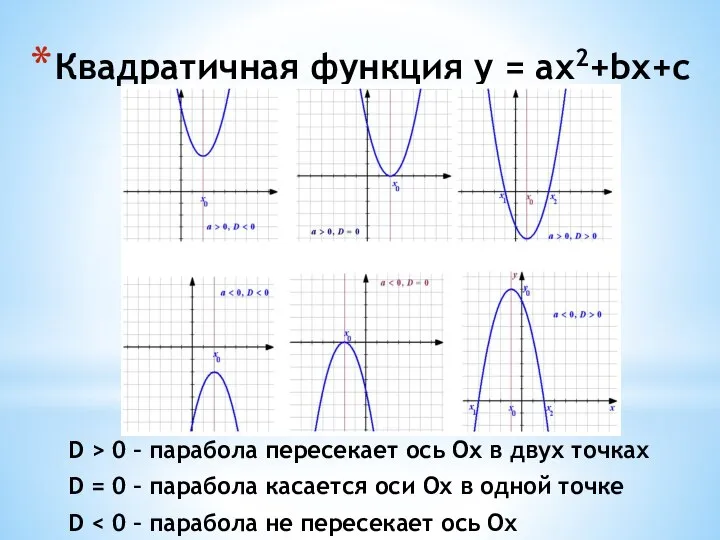
- 10. Квадратичная функция y = аx2 + bx + c
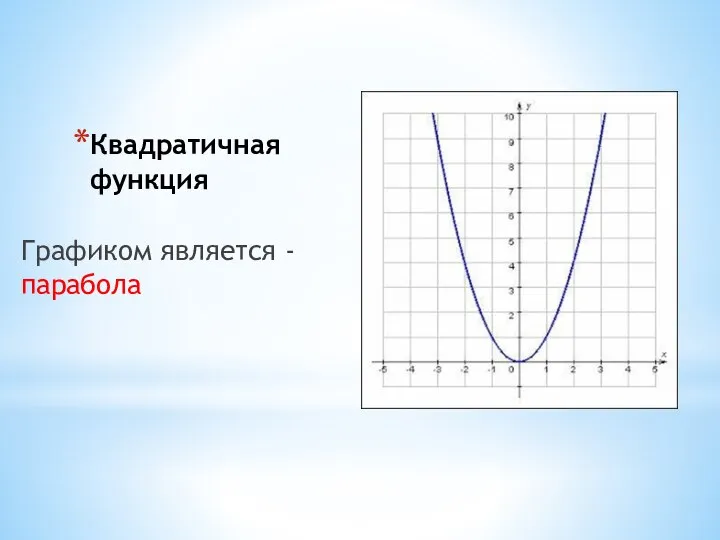
- 11. Квадратичная функция Графиком является - парабола
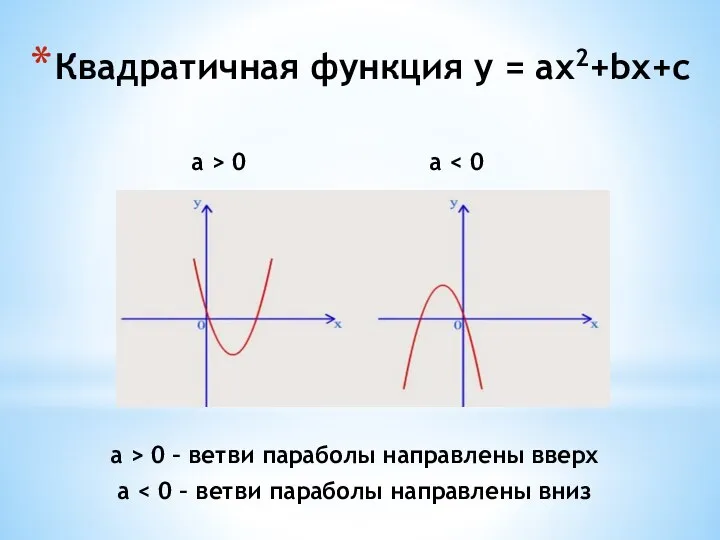
- 12. a > 0 a Квадратичная функция y = ax2+bx+с a > 0 – ветви параболы направлены
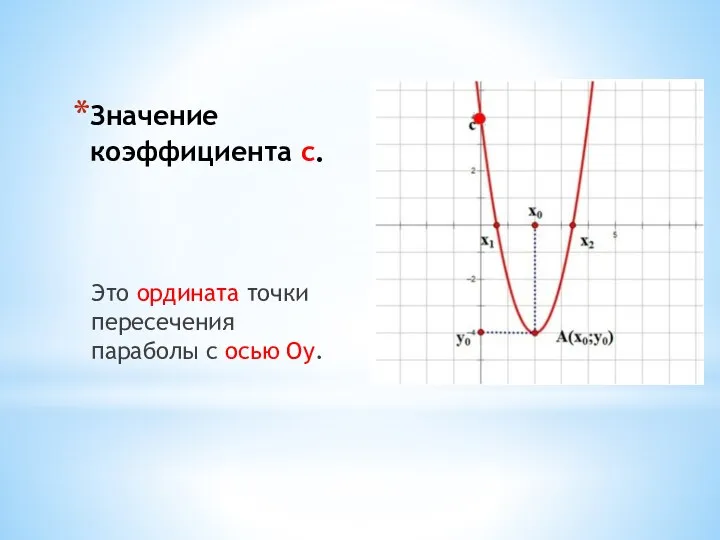
- 13. Значение коэффициента с. Это ордината точки пересечения параболы с осью Оy.
- 14. c > 0 c Квадратичная функция y = ax2+bx+с c > 0 – парабола пересекает ось
- 15. Квадратичная функция y = ax2+bx+с D > 0 – парабола пересекает ось Ox в двух точках
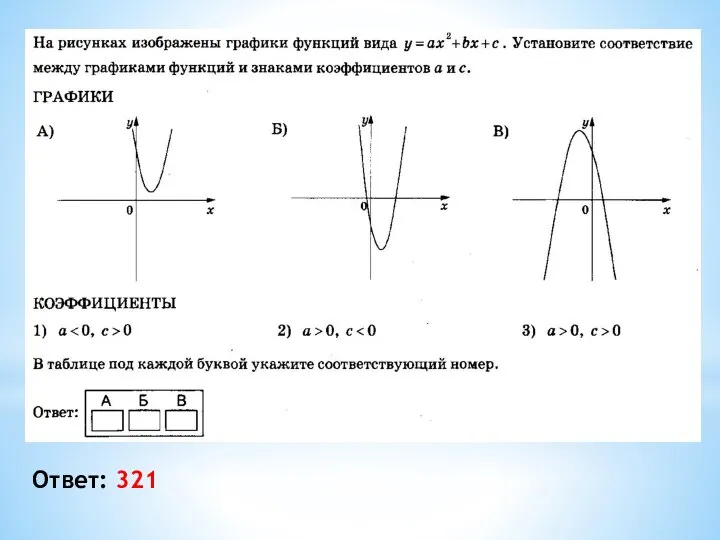
- 16. Ответ: 321
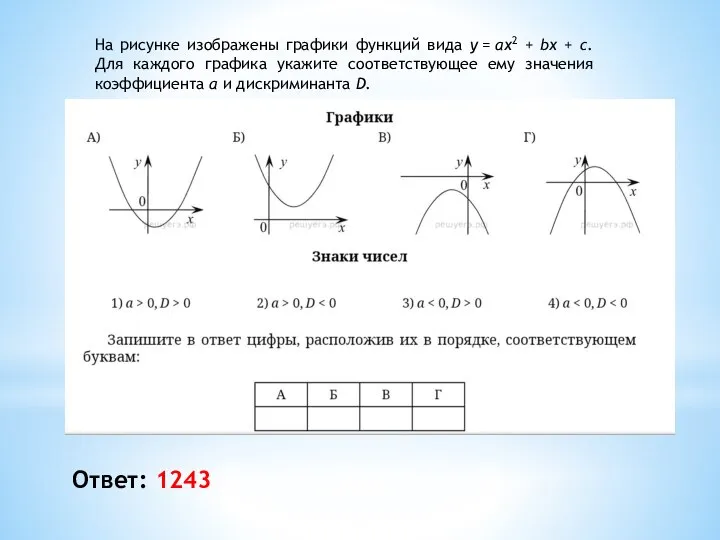
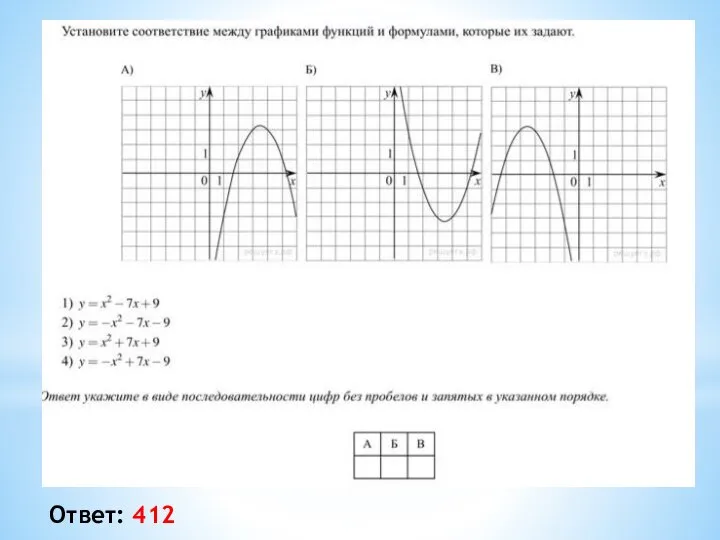
- 17. На рисунке изображены графики функций вида y = ax2 + bx + c. Для каждого графика
- 18. Ответ: 412
- 19. Функция обратной пропорциональной зависимости
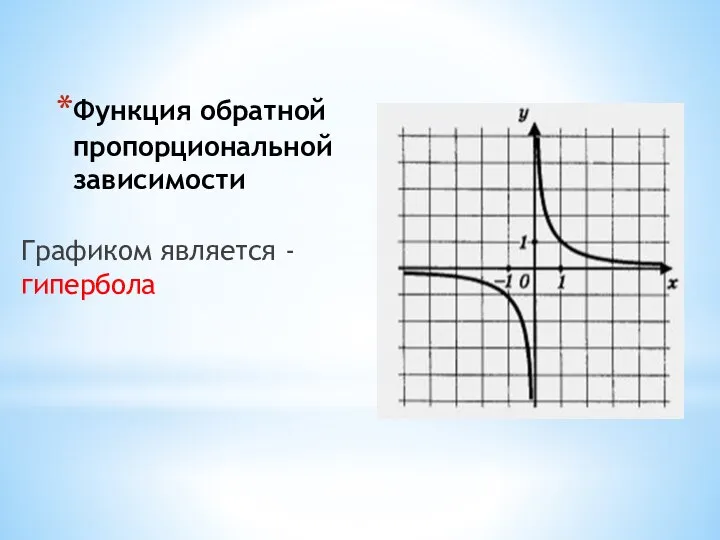
- 20. Функция обратной пропорциональной зависимости Графиком является - гипербола
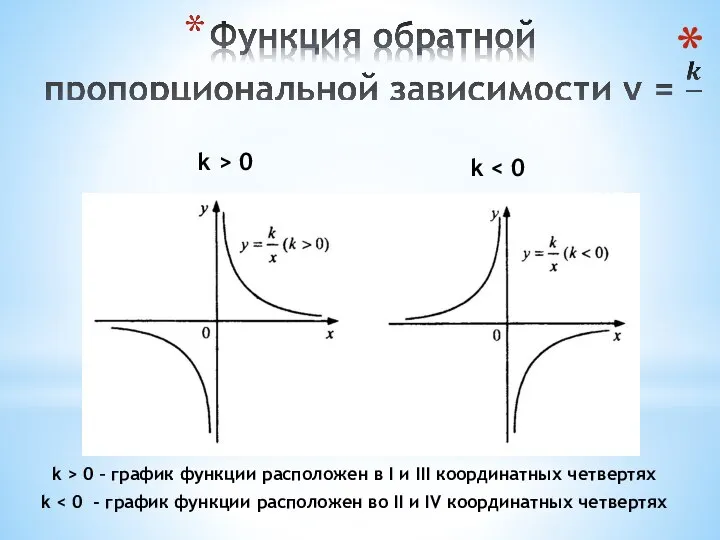
- 21. k > 0 k k > 0 – график функции расположен в I и III координатных
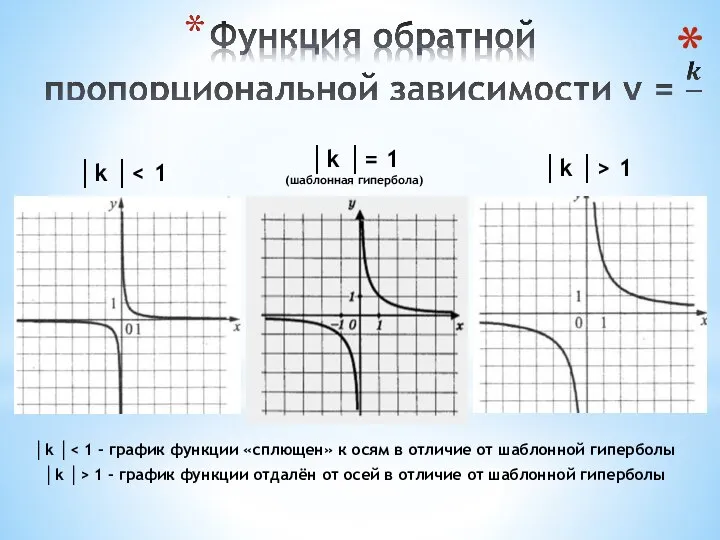
- 22. │k │ │k │> 1 │k │ │k │> 1 - график функции отдалён от осей
- 23. Ответ: 213
- 24. Ответ: 231
- 25. Степенная функция
- 26. Степенная функция Графиком является – ветвь параболы
- 27. Ответ: 132
- 28. Ответ: 213
- 30. Скачать презентацию








 Программирование графики
Программирование графики Свойства функций
Свойства функций Примеры +7, +8, +9
Примеры +7, +8, +9 Конус. Площадь поверхности конуса
Конус. Площадь поверхности конуса Понятие области
Понятие области Карточки по математике. Состав числа
Карточки по математике. Состав числа Построение графиков с модулем
Построение графиков с модулем Точки экстремума
Точки экстремума Backpropagation
Backpropagation Тригонометрические функции y = tg x и y = ctg x, их свойства и графики
Тригонометрические функции y = tg x и y = ctg x, их свойства и графики Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса
Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса Проценты. Определение
Проценты. Определение Вариация управления
Вариация управления Порядок выполнения действий в выражениях
Порядок выполнения действий в выражениях Урок-игра Новогодний серпантин. 6 класс
Урок-игра Новогодний серпантин. 6 класс 5dc68842a93b54ac
5dc68842a93b54ac Таблица умножения с Лунтиком
Таблица умножения с Лунтиком Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Уравнения. 3 класс
Уравнения. 3 класс Рубежный (итоговый) контроль по математике в 6-х классах образовательных учреждений г.Москвы апрель 2007 года
Рубежный (итоговый) контроль по математике в 6-х классах образовательных учреждений г.Москвы апрель 2007 года Решение текстовых задач с использованием квадратных уравнений
Решение текстовых задач с использованием квадратных уравнений Функциональные и степенные ряды
Функциональные и степенные ряды Что? Где? Когда?
Что? Где? Когда? Увеличение и уменьшение числа на несколько единиц, сравнивание длины отрезков. 1 класс
Увеличение и уменьшение числа на несколько единиц, сравнивание длины отрезков. 1 класс Сравнение моделей
Сравнение моделей Система пропорционирования в проектировании объектов дизайна
Система пропорционирования в проектировании объектов дизайна Среднее арифметическое. Среднее значение величины
Среднее арифметическое. Среднее значение величины Разработка параллельного метода вычислений
Разработка параллельного метода вычислений