Содержание
- 2. Найденные древние вавилонские глиняные таблички, датированные где-то между 1800 и 1600 годами до н.э., являются самыми
- 3. Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был Брахмагупта (Индия,
- 4. Задачи на квадратные уравнения встречались уже в 499 г. в Древней Индии. Часто они были в
- 5. Формулы решения квадратных уравнений в Европе были впервые изложены в “Книге абака”, написанной в 1202 году
- 6. Пусть дано квадратное уравнение ах2+вх+с=0, где а≠0. 1.Если а+в+с=0(т.е.сумма коэффициентов уравнения равна нулю), то х1=1,х2=с/а. Например:345х2-137х-208=0(345-137-208=0),значит
- 7. 1.5х2-7х+2=0; 2.3х2+5х-8=0; 3.11х2+25х-36=0; 4.11х2+27х+16=0; 5.939х2+978х+39=0. Задание . Решите уравнения:
- 9. Скачать презентацию






 Средние величины. (Лекция 4.2)
Средние величины. (Лекция 4.2) Элементы математической логики
Элементы математической логики Презентация на тему Правила дифференцирования
Презентация на тему Правила дифференцирования  Таблицы, часть 2, 9-11 классы
Таблицы, часть 2, 9-11 классы Цилиндр. Цилиндр в архитектуре города Хабаровска
Цилиндр. Цилиндр в архитектуре города Хабаровска Площадь четырёхугольника
Площадь четырёхугольника Интерактивная игра Состав числа в пределах первого десятка
Интерактивная игра Состав числа в пределах первого десятка Простейшие преобразования графиков
Простейшие преобразования графиков Деление одночлена на одночлен
Деление одночлена на одночлен Формула Стирлинга
Формула Стирлинга Запись многозначных чисел
Запись многозначных чисел Функции и предупреждающие знаки дорожного движения. 11 класс
Функции и предупреждающие знаки дорожного движения. 11 класс Многогранники. Виды многогранников
Многогранники. Виды многогранников Логика. Введение
Логика. Введение Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Производная функции
Производная функции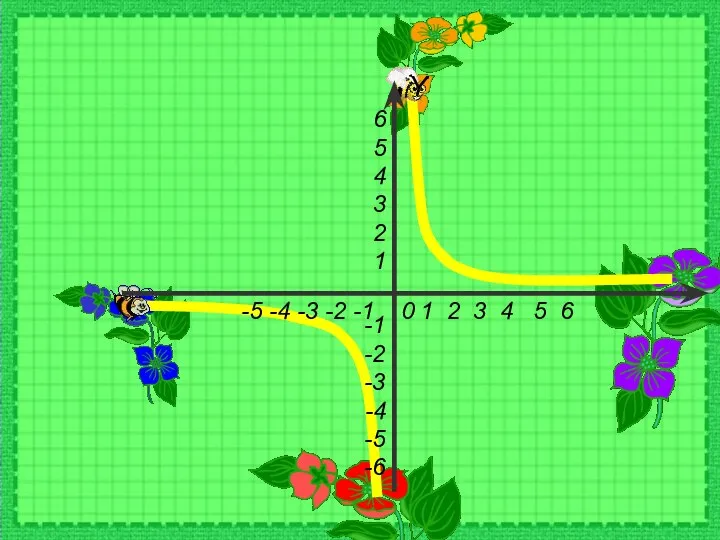 Функция у=1/х и её график
Функция у=1/х и её график Корни. Формулы
Корни. Формулы Вырезаем квадрат
Вырезаем квадрат Основные формулы для Огэ по математике
Основные формулы для Огэ по математике Решаем задачи
Решаем задачи Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Задачи с параметром в материалах ГИА и методы их решения (по материалам ЕГЭ за последние 5 лет)
Задачи с параметром в материалах ГИА и методы их решения (по материалам ЕГЭ за последние 5 лет) Системы уравнений. Задание №9. ОГЭ
Системы уравнений. Задание №9. ОГЭ Prezentado de enspezoj
Prezentado de enspezoj ДНФ и импликанты
ДНФ и импликанты Парная регрессия и корреляция
Парная регрессия и корреляция Первообразная и неопределённый интеграл. Лекция 2
Первообразная и неопределённый интеграл. Лекция 2