- Главная
- Математика
- Средние величины и показатели вариации

Содержание
- 2. «1» Каждая единица совокупности характеризуется своим признаком (показателем), который отличается от других единиц. Например: зарплата –
- 3. Основные элементы средних величин: Варианта (х) – столбец (признак), из которого рассчитывается средняя величина. Частота (весы)
- 4. «2» В зависимости от исходной информации различают несколько видов средних величин: средняя арифметическая: а) простая –
- 5. б) взвешенная - вычисляется в том случае, если признак, из которого вычисляется средняя, встречается неодинаковое число
- 6. средняя гармоническая: а) взвешенная – вычисляется в том случае, если даны варианты (х) и произведение (W)
- 7. средняя хронологическая (простая) – вычисляется в моментном динамическом ряду с равными интервалами времени: _ ½ х1
- 8. средняя геометрическая – применяется для расчёта среднего темпа роста (тенденции) в рядах динамики: _ n _
- 9. средняя прогрессивная – формула также выбирается исходя из имеющихся данных (арифметическая или гармоническая). Принцип расчёта заключается
- 10. «3» Информации о средних уровнях исследуемых показателей обычно бывает недостаточно для анализа экономических явлений или процессов.
- 11. Например: Рассмотрим вариацию урожайности зерновых по 10 хозяйствам Лукояновского района Нижегородской области: Для того, чтобы правильно
- 12. Среднее линейное отклонение - это средняя арифметическая из абсолютных отклонений вариант от их средней: _ _
- 13. Дисперсия – это квадрат среднего квадратического отклонения. Единиц измерения не имеет, используется в дисперсионном анализе. _
- 14. _ ∑ х∙f 50785 х = ------ = ---------- = 16, 7 (ц/га) – средняя урожайность
- 16. Скачать презентацию
Слайд 2 «1»
Каждая единица совокупности характеризуется своим признаком (показателем), который отличается
«1»
Каждая единица совокупности характеризуется своим признаком (показателем), который отличается

Например: зарплата – Иванова – 15000 руб. (х1)
Петрова – 12000 руб. (х2) } индивидуальные
Сидорова - 13000 руб.(х3) величины -
А для характеристики совокупности в целом рассчитывают среднюю величину (Х).
Средние величины - это обобщающие показатели, выражающие типичные размеры варьирующих признаков качественно однородных общественных явлений.
Для правильного исчисления средней необходимы следующие условия:
совокупность должна быть достаточно большой (массовой);
совокупность должна быть однородной;
если совокупность разнородна, то её нужно разделить на однородные группы и для каждой группы исчислить свою среднюю величину.
Например: зарплата, руб.
5600 _
5800 } х1 = 5833,3 руб.
6100
9200 _
10400 } х 2 = 10366,7 руб.
11500
18900 _
21300 } х3 =20933,3 руб.
22600
Слайд 3
Основные элементы средних величин:
Варианта (х) – столбец (признак),
Основные элементы средних величин:
Варианта (х) – столбец (признак),

Частота (весы) (f) – столбец, который показывает, сколько раз повторяется данный
признак (варианта).
n – число единиц совокупности (может быть равен ∑f).
W = х · f - это произведение варианты и частоты.
Например: х- урожайность, ц/га
f- посевная площадь, га
W – валовый сбор, ц
или х – зарплата 1 работника, руб.
f- количество работников, чел.
W – общий фонд зарплаты, руб. и т.п.
зарплата
n (f) (варианта -Х)
Например: Иванов – 15000 руб.
Петров – 12000 руб.
Сидоров - 13000 руб.
∑f = n = 3 ∑х = 40000
Слайд 4 «2»
В зависимости от исходной информации различают несколько видов средних
«2»
В зависимости от исходной информации различают несколько видов средних

средняя арифметическая:
а) простая – вычисляется в том случае, если признак, из которого вычисляется средняя, встречается один или одинаковое число раз.
_ ∑х х1 + х2 +…+ хn
х = ----- = --------------------
n n
Например: зарплата по бригаде, руб.
Иванов – 15000
Петров - 12000
Сидоров – 13000
Решение: _ 15000+12000+13000
Х = ----------------------------- = 13333,33 руб. – средняя зарплата 1 работника
3
Например: Квартал Производство хлеба, т
1 256
2 284
3 292
4 301
Решение: _ 256 + 284 +292+301
Х = ----------------------------- = 283 т – среднеквартальный объём производства хлеба
4
Слайд 5
б) взвешенная - вычисляется в том случае, если признак, из которого
б) взвешенная - вычисляется в том случае, если признак, из которого

_ ∑х∙f х1·f1+х2∙f2+…+хn·fn
х = ------- = ------------------------
∑f f1 + f2 + … + f n
Например:
_ 15200 ·3 + 16400 ·6 +17400 ·4
Решение: х = --------------------------------------------= 16431 руб. – средняя зарплата 1 работника
3 + 6 + 4
Например:
_ 15 · 190 + 18 · 210 + 16 · 250 10630
Решение: х = ----------------------------------------- = --------- = 16,4 (ц/га) – средняя урожайность зерновых
190 + 210 + 250 650
Слайд 6
средняя гармоническая:
а) взвешенная – вычисляется в том случае, если
средняя гармоническая:
а) взвешенная – вычисляется в том случае, если

_ ∑ W W1 + W2 + … +Wn
х = ------- = ----------------------------
∑ W W1 W2 Wn
х ---- + ---- + … + ----
х1 х2 Хn
Например:
_ 1600 + 2400 + 3750 7750
Решение: х = ---------------------------- = -------- = 12,7 (ц/га)
1600 2400 3750 610
------- + ------- + -------
10 12 15
б) простая - встречается и используется очень редко
_ n
х = ------
∑ 1
х
Слайд 7 средняя хронологическая (простая) – вычисляется в моментном динамическом ряду с равными
средняя хронологическая (простая) – вычисляется в моментном динамическом ряду с равными

_ ½ х1 + х2 + х3 + … +½хn
х = ----------------------------------
n – 1
где n – число периодов
Например: имеется численность работников на:
1.01.- 126 чел.
1.02.- 132 чел.
1.03.- 138 чел.
1.04.- 129 чел.
Определить среднюю численность работников за 1 квартал?
_ ½·126 + 132+138+½∙129
Решение: х = --------------------------------- = 133 (чел.) – средняя численность работников
4 - 1 за 1 квартал
средняя хронологическая (взвешенная) – вычисляется в моментном динамическом ряду с разными интервалами времени:
_ (х1+х2)∙f1 +(х2+х3)∙f2 + …+ (хn-1 + хn)∙fn-1
х = ---------------------------------------------------
2∑f
где f – промежуток времени между датами (см. тему «Ряды динамики»)
Слайд 8 средняя геометрическая – применяется для расчёта среднего темпа роста (тенденции) в
средняя геометрическая – применяется для расчёта среднего темпа роста (тенденции) в
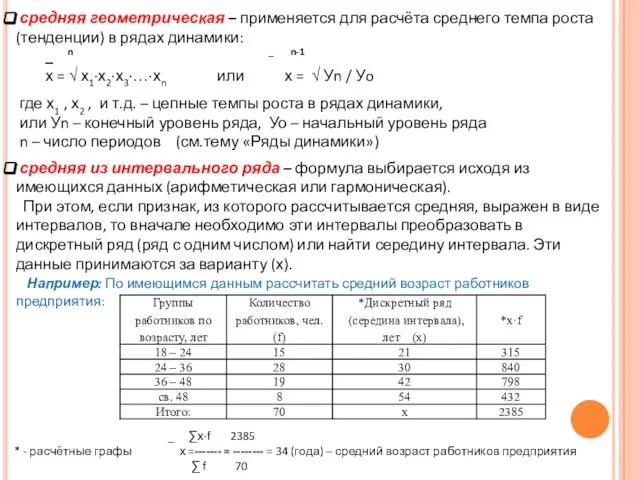
_ n _ n-1
х = √ х1·х2∙х3·…·хn или х = √ Уn / Уo
где х1 , х2 , и т.д. – цепные темпы роста в рядах динамики,
или Уn – конечный уровень ряда, Уо – начальный уровень ряда
n – число периодов (см.тему «Ряды динамики»)
средняя из интервального ряда – формула выбирается исходя из имеющихся данных (арифметическая или гармоническая).
При этом, если признак, из которого рассчитывается средняя, выражен в виде интервалов, то вначале необходимо эти интервалы преобразовать в дискретный ряд (ряд с одним числом) или найти середину интервала. Эти данные принимаются за варианту (х).
Например: По имеющимся данным рассчитать средний возраст работников предприятия:
_ ∑х∙f 2385
* - расчётные графы х =------- = -------- = 34 (года) – средний возраст работников предприятия
∑ f 70
Слайд 9 средняя прогрессивная – формула также выбирается исходя из имеющихся данных (арифметическая
средняя прогрессивная – формула также выбирается исходя из имеющихся данных (арифметическая

Принцип расчёта заключается в том , что берутся не все данные условия, а выбираются наилучшие показатели варианты.
Например: По имеющимся данным рассчитать среднюю прогрессивную сменную выработку:
* - наилучшие данные по сменной выработке 1 работника
_ ∑ W 540 + 375 + 492 + 420
х = ------- = ------------------------------- = 76 (дет.) – средняя прогрессивная сменная
∑ W 540 375 492 420 выработка 1 работника
х ----- + ----- + ---- + -----
90 75 82 60
Слайд 10
«3»
Информации о средних уровнях исследуемых показателей обычно бывает недостаточно
«3»
Информации о средних уровнях исследуемых показателей обычно бывает недостаточно

Так, например, если взять совокупность из 10-30 с./х.-предриятий района и сравнить по ним такие показатели, как: урожайность культур, продуктивность животных, трудоёмкость или себестоимость 1 ц продукции, то эти показатели будут отличаться при переходе от одного хозяйства к другому, т.к. зависят от многочисленных факторов, влияющих на них. А сочетание этих факторов в хозяйствах различно, поэтому и результаты будут различаться (варьировать).
Например: На урожайность влияют следующие факторы: сорт семян, их качество, состав почвы, количество вносимых удобрений, сроки и качество работ, климатические условия и т.д.
На продуктивность коров влияет: уровень и качество кормления, условия содержания, породный и возрастной состав животных и т.д.
Чем лучше сочетание этих факторов, тем выше и результат.
Однако на практике, такое сочетание редко, поэтому показатели колеблются (варьируют).
В связи с этим, рассматриваемая совокупность по данному признаку может быть однородной или разнородной. А вот чем однороднее совокупность, тем меньше будет и вариация признака.
Слайд 11Например: Рассмотрим вариацию урожайности зерновых по 10 хозяйствам Лукояновского района Нижегородской области:
Например: Рассмотрим вариацию урожайности зерновых по 10 хозяйствам Лукояновского района Нижегородской области:

Размах вариации – это разность между максимальным и минимальным значениями признака:
R = Хmax - Х min
Слайд 12 Среднее линейное отклонение - это средняя арифметическая из абсолютных отклонений вариант
Среднее линейное отклонение - это средняя арифметическая из абсолютных отклонений вариант

_
_ ∑| х – х |
для не взвешенного ряда - d = ------------
n
_
_ ∑|х – х |∙f
для взвешенного ряда - d = --------------
∑f
Единицы измерения те же, что и у показателя (например, ц/га)
Среднее квадратическое отклонение – наиболее точно характеризует отклонение вариант от средней величины.
Имеет ту же размерность, что и изучаемый признак, например: ц/га.
_
∑ ( х – х )2
σ = √ -------------- - для не взвешенного ряда
n
_
∑ ( х – х )2 ∙ f
σ= √ ------------------ - для взвешенного ряда
∑ f
Слайд 13 Дисперсия – это квадрат среднего квадратического отклонения.
Единиц измерения не
Дисперсия – это квадрат среднего квадратического отклонения.
Единиц измерения не
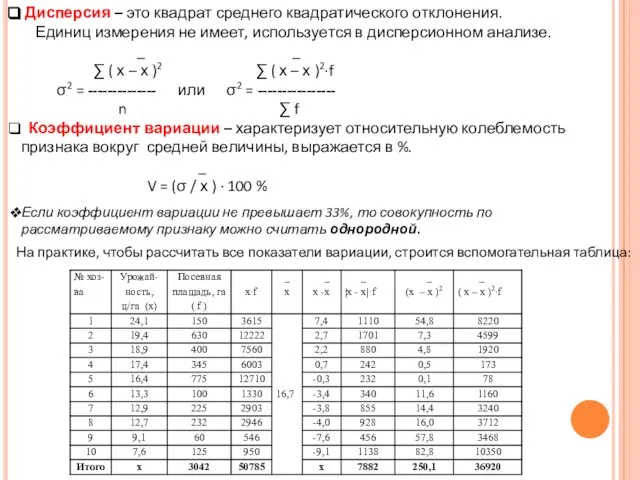
_ _
∑ ( х – х )2 ∑ ( х – х )2∙f
σ2 = -------------- или σ2 = ----------------
n ∑ f
Коэффициент вариации – характеризует относительную колеблемость признака вокруг средней величины, выражается в %.
_
V = (σ / х ) ∙ 100 %
Если коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.
На практике, чтобы рассчитать все показатели вариации, строится вспомогательная таблица:
Слайд 14
_ ∑ х∙f 50785
х = ------ = ---------- = 16, 7
_ ∑ х∙f 50785
х = ------ = ---------- = 16, 7

∑ f 3042
R = Хmax – Хmin = 24,1 – 7,6 = 16,5 (ц/га) – размах вариации
_
_ ∑|х – х | · f 7882
d = -------------- = ------- = 2,6 (ц/га) – среднее линейное отклонение
∑ f 3042
_ 2
2 ∑ ( х – х ) ∙ f 36920
σ = -------------- = --------- = 12,1 - дисперсия
∑ f 3042
_ 2
∑ (х – х ) · f 36920
σ = √ ------------- = √ ----------- =√ 12,1 =3,5 (ц/га) – среднее квадратическое отклонение
∑ f 3042
_
V = (σ/ х ) ∙ 100 % = 3,5 : 16,7 · 100% = 21(%) – коэффициент вариации
На основании произведённых расчётов можно сделать следующие выводы:
Урожайность по 10 хозяйствам района варьирует от 7,6 до 24,1 ц/га.
Размах вариации составляет 16,5 ц/га. Средняя урожайность составляет 16,7 ц/га.
В целом по данной совокупности хозяйств урожайность отклоняется от среднего уровня
на 3,5 ц/га или на 21%.
В данном случае коэффициент вариации характеризует небольшую колеблемость урожайности вокруг её средней величины, т.е. совокупность по урожайности можно считать однородной.
 Аналоги теореми порівняння Колмогорова та їх застосування
Аналоги теореми порівняння Колмогорова та їх застосування Бутылка Клейна
Бутылка Клейна Устный счет
Устный счет Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Прямоугольный параллелепипед
Прямоугольный параллелепипед Кругові приклади
Кругові приклади Сложение и вычитание вида +1 и -1
Сложение и вычитание вида +1 и -1 Состав чисел в пределах 10. Закрепление пройденного
Состав чисел в пределах 10. Закрепление пройденного Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Сумма углов в треугольнике
Сумма углов в треугольнике Приближение десятичных дробей
Приближение десятичных дробей Порядок действий в примерах (для младших школьников)
Порядок действий в примерах (для младших школьников) Логика предикатов
Логика предикатов Готовимся к ЕГЭ. Базовый уровень
Готовимся к ЕГЭ. Базовый уровень Аппликации из геометрических фигур
Аппликации из геометрических фигур Треугольники. Решение задач
Треугольники. Решение задач Обработка результатов измерения отклонений от круглости
Обработка результатов измерения отклонений от круглости Углы, связанные с окружностью
Углы, связанные с окружностью Величины
Величины Презентация на тему Число и цифра 4
Презентация на тему Число и цифра 4  Выберите чётные числа (триггеры)
Выберите чётные числа (триггеры) Подготовка к ОГЭ, 9 класс, геометрия
Подготовка к ОГЭ, 9 класс, геометрия Моделирование вероятности столкновения судов
Моделирование вероятности столкновения судов 2.1._-_
2.1._-_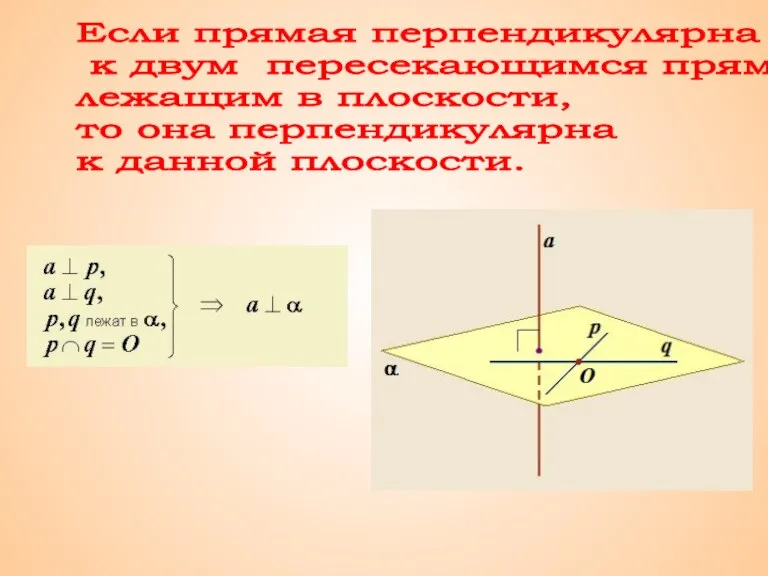 Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Основы метрологического обеспечения
Основы метрологического обеспечения Смежные и вертикальные углы
Смежные и вертикальные углы