Векторы на плоскости. Понятие вектора. Равенство векторов

Векторы на плоскости
Понятие вектора. Равенство векторов
Векторные величины в отличие от скалярных имеют не только числовое значение, но и направление в пространстве.
Сонаправленные вектора – коллинеарные векторы, имеющие одинаковые направления.
А В
С D
Противоположно направленные вектора – коллинеарные векторы, имеющие разные направления.
T E
V L

Вектор – это направленный отрезок. Вектор обозначают двумя заглавными буквами (соответствующие началу и концу вектора) со стрелкой над ними или одной прописной буквой со стрелкой над ней.
Если векторы лежат на перпендикулярных прямых, то их называют ортогональными.

Векторы называют равными, если они сонаправлены и их модули равны. A B
R K
Вектор АВ = вектору RK.
Равные векторы можно совместить параллельным переносом, и, обратно, если векторы совмещаются параллельным переносом, то эти векторы равны.
Модулем вектора АВ называют длину отрезка АВ.
Нулевой вектор – вектор, начало и конец которого совпадают. Его обозначают нулём со стрелкой над ним. Любую точку плоскости можно рассматривать как нулевой вектор.

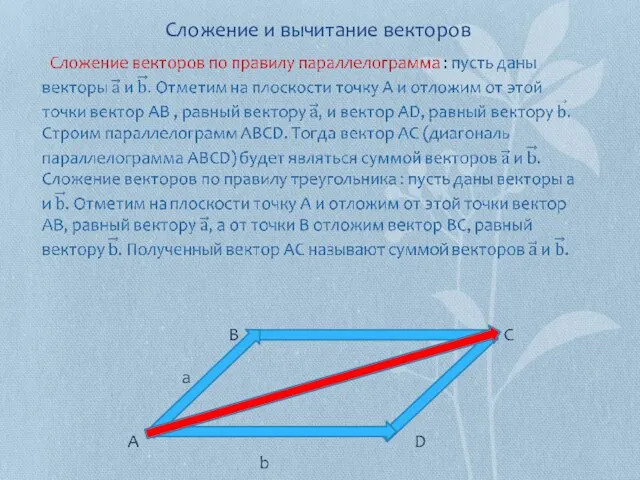
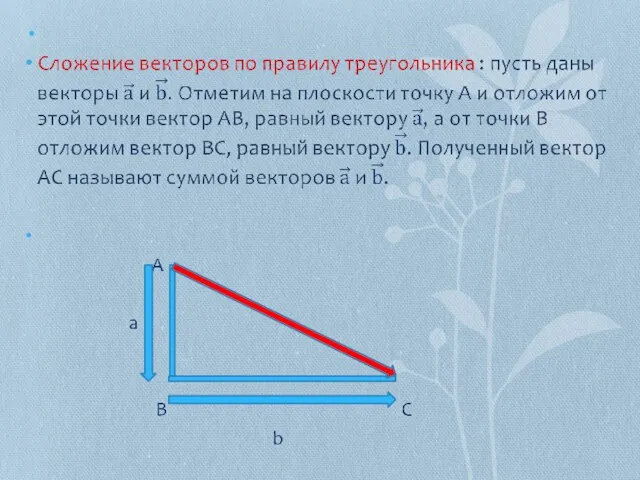
Сложение и вычитание векторов

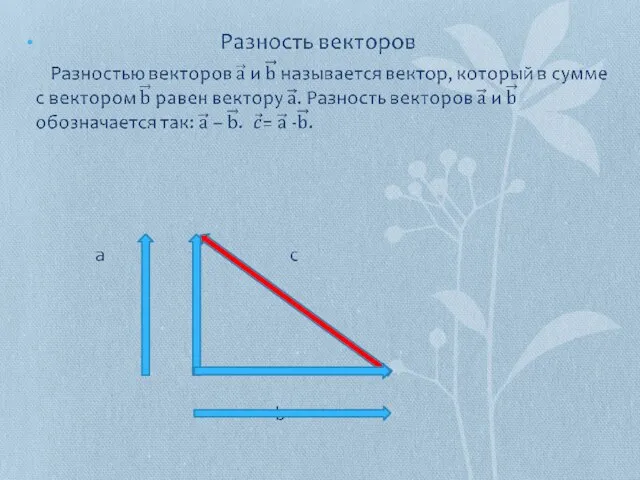
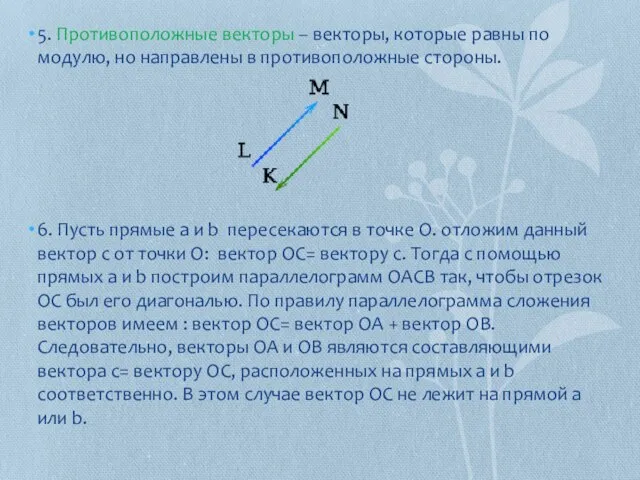
5. Противоположные векторы – векторы, которые равны по модулю, но направлены в противоположные стороны.
6. Пусть прямые a и b пересекаются в точке О. отложим данный вектор с от точки О: вектор ОС= вектору с. Тогда с помощью прямых а и b построим параллелограмм ОАСВ так, чтобы отрезок ОС был его диагональю. По правилу параллелограмма сложения векторов имеем : вектор ОС= вектор ОА + вектор ОВ. Следовательно, векторы ОА и ОВ являются составляющими вектора с= вектору ОС, расположенных на прямых а и b соответственно. В этом случае вектор ОС не лежит на прямой а или b.

Умножение вектора на число

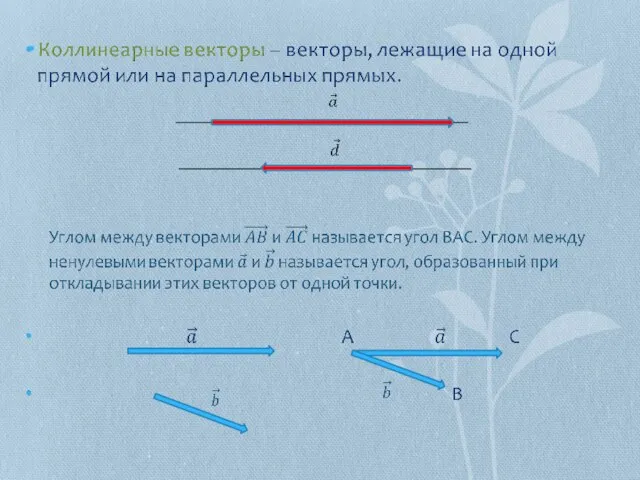
Угол между векторами, скалярное произведение векторов

Координаты вектора
1. Теорема о разложении вектора по двум неколлинеарным векторам:
Если нулевые векторы а и b не коллинеарны, то для любого вектора с найдутся числа х и y такие, что выполняется равенство c=ха+yb, причём коэффициенты разложения х и y определяются единственным образом.
Доказательство:
На плоскости отложим от точки О векторы а, b и с. Концы векторов соответственно обозначим через А, В, С. Тогда по теореме о разложении вектора на составляющие по двум пересекающимся прямым, вдоль прямых ОА и ОВ найдутся единственные векторы ОА’ и ОИ’ такие, что ОС=ОА’+OB’.
Так как вектор ОА коллинеарен вектору ОА’ и вектор ОВ коллинеарен вектору ОВ’, то по теореме о коллинеарных векторах существуют единственные действительные числа х и y, что вектор ОА=хОА=ха и вектор ОВ=yOB=yb. Поэтому из равенства ОС=ОА+ОВ следует единственное представление вида с=ОС=ха+yb. Теорема доказана.
Базисные векторы - выбранные на плоскости два неколлинеарных вектора, по которым производится разложение заданного вектора.
Любые два неколлинеарных вектора можно приять в качестве базисных векторов и любой вектор этой плоскости однозначно разлагается по этим базисным векторам. В доказанной теореме векторы а и b – базисные векторы, а действительные числа х и y называются координатами вектора с в базисе векторов а и b.

Свойства координат вектора

Направляющий вектор прямой- это любой ненулевой вектор, лежащий на данной прямой или на параллельной ей прямой.
Уравнение прямой , проходящий через две заданные точки (x1,y1) и (x2,y2), записывается так:
Вектор нормали- это вектор, который перпендикулярен данной плоскости .
Уравнение прямой по вектору нормали: а(х-х0)+в(у-у0)=0
Формула, по которой можно определить угол между прямыми :
Расстояние от точки до прямой равно длине перпендикуляра опущенного из точки на прямую.

Выражение скалярного произведения через координаты векторов