Содержание
- 2. Титульный лист Творческая работа Коноховой Елены ученицы 8 класса МОУ «СОШ с.Петропавловка Саратовской области Дергачёвского района»
- 3. Предисловие Многие знают, что такое лента (лист) Мёбиуса. Тем, кто ещё не знаком с удивительным листом,
- 4. Таинственный и знаменитый лист Мёбиуса (иногда говорят : лента Мёбиуса) придумал в 1858г. немецкий геометр Август
- 5. Лист Мёбиуса – один из объектов области математики под названием «топология» (по-другому – «геометрия положений»). Удивительные
- 6. Рассказывают, что открыть свой «лист» Мёбиусу помогла служанка, сшившая однажды неправильно концы ленты. Легенда
- 7. Увлекательное исследование Запаситесь несколькими листами обычной белой бумаги, клеем и ножницами.
- 8. Берем бумажную ленту АВСD. Прикладываем ее концы АВ и СD друг к другу и склеиваем. Но
- 9. Получим такое перекрученное кольцо
- 10. ? Зададимся вопросом: сколько сторон у этого куска бумаги? Две, как у любого другого? А ничего
- 11. Красим, не отрываемся, на другую сторону не переходим. Красим... Закрасили? А где же вторая, чистая сторона?
- 12. Теперь второй вопрос. Что будет, если разрезать обычный лист бумаги? Конечно же, два обычных листа бумаги.
- 13. А вот что получилось у меня Лента перекручена два раза
- 14. Теперь сделайте новый лист Мёбиуса и скажите, что будет, если разрезать его вдоль, но не посередине,
- 15. А вот что получилось у меня
- 16. А если на три части? Три ленты? А ничего подобного! ?
- 17. Получим два сцепленных кольца. Одно из них вдвое длиннее исходного и перекручено два раза. Второе- лист
- 18. Человечек - перевертыш. Вырежьте бумажного человечка и отправьте его вдоль пунктира, идущего посередине листа Мёбиуса.
- 19. Он вернулся к месту старта. Но в каком виде! В перевернутом! А чтобы он вернулся к
- 20. Исследуйте дальше эту поразительную (и тем не менее совершенно реальную) одностороннюю поверхность, и вы получите море
- 22. Скачать презентацию


















 Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша
Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша Приемы вычитания с переходом на десяток
Приемы вычитания с переходом на десяток Функция y=ctg x. График
Функция y=ctg x. График Матрицы и определители
Матрицы и определители Дифференциальное исчисление в нормированных пространствах
Дифференциальное исчисление в нормированных пространствах Элементы теории обобщенных функций
Элементы теории обобщенных функций ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Механический смысл производной. Задания для устного счета
Механический смысл производной. Задания для устного счета Умножение. Координаты точки
Умножение. Координаты точки Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Решение задач на дроби
Решение задач на дроби Равенство
Равенство Случаи вычитания 11-
Случаи вычитания 11- Веселые ромашки
Веселые ромашки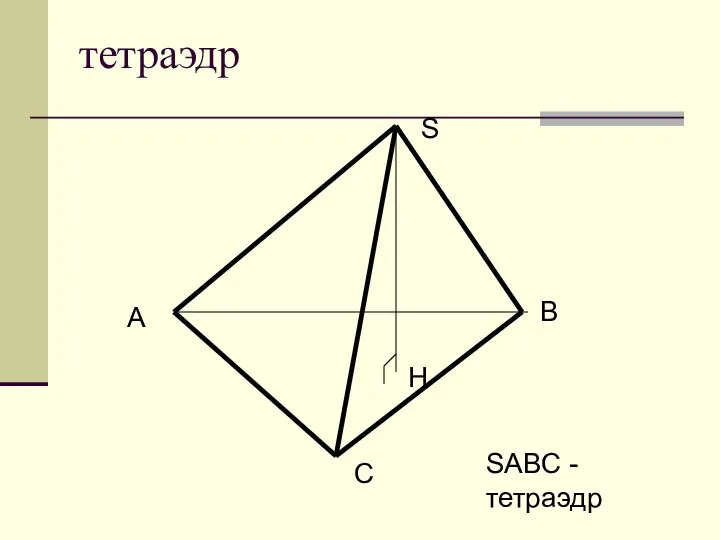 Тетраэдр
Тетраэдр Векторы. Направление вектора
Векторы. Направление вектора Изоморфные графы
Изоморфные графы Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины Игры. Памятка
Игры. Памятка Многоугольники в жизни
Многоугольники в жизни Методический материал по алгебре
Методический материал по алгебре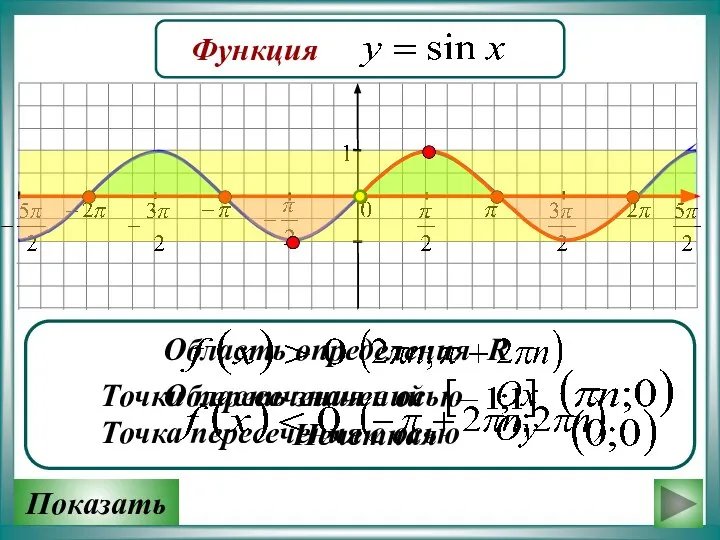 График функции y = sin x
График функции y = sin x Путешествие по морям
Путешествие по морям Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Площадь параллелограмма
Площадь параллелограмма Смежные углы
Смежные углы Сложение целых чисел
Сложение целых чисел Понятие интеграла
Понятие интеграла