Содержание
- 2. Приведение и использование погрешностей
- 6. Число δх называется погрешностью или ошибкой измерения в измерении х.
- 7. Абсолютная погрешность — понимают разность между точным (истинным) значением величины xист и ее приближенным (измеренным) значением
- 8. Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерений ∆x к истинному значению xист измеряемой
- 9. Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному
- 10. Если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то xнорм определяется равным верхнему
- 11. Значащие цифры
- 13. Погрешность в любой измеренной величине имеет ту же размерность, что и сама измеренная величина.
- 14. Различие
- 15. Сравнение двух измеренных значений
- 17. Относительные погрешности Качество измерения характеризуется на только самой погрешностью δх, но также и отношением δх к
- 19. Погрешность в произведении
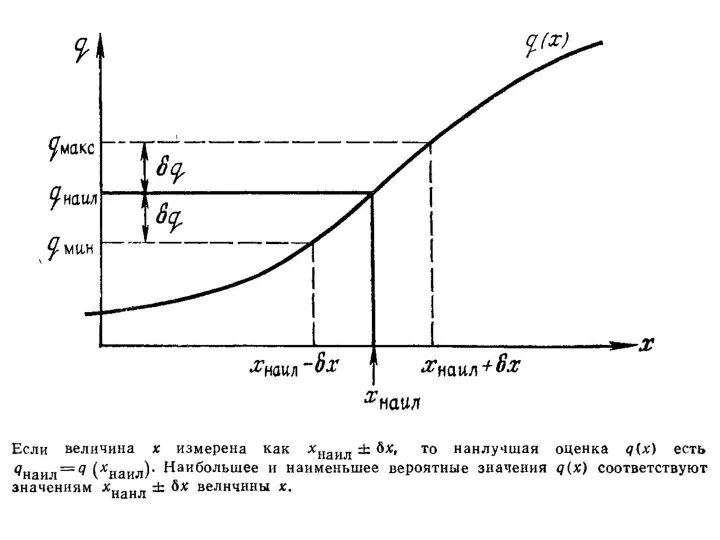
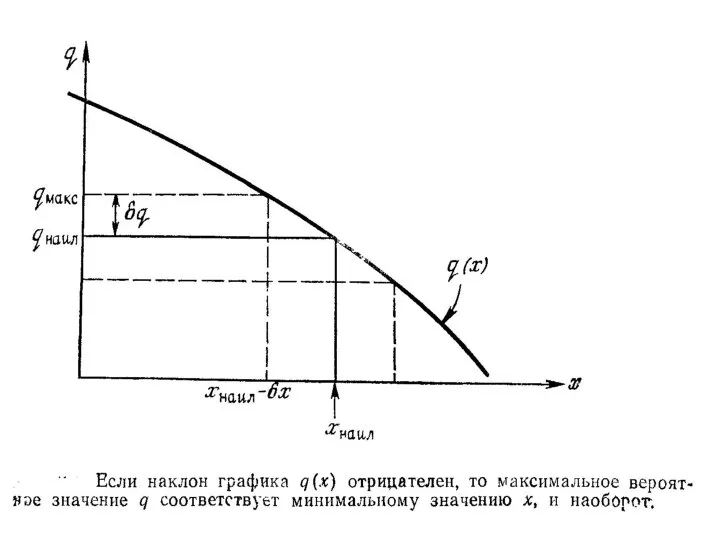
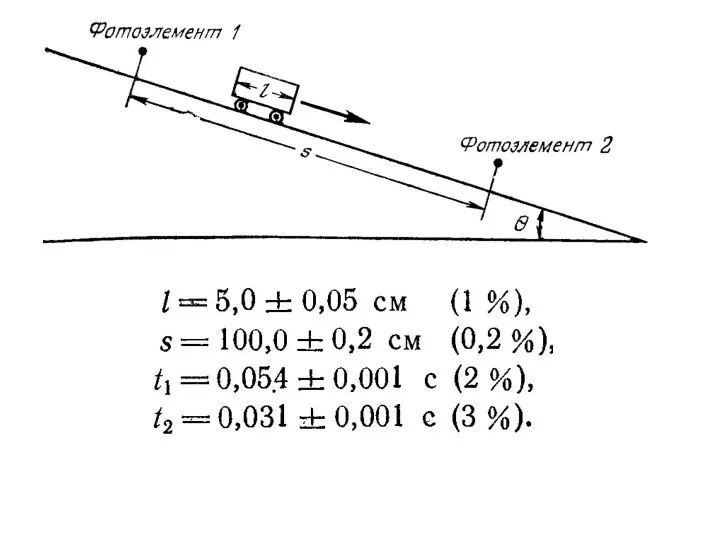
- 21. Погрешности в косвенных измерениях Если измеряются две величины х и у и вычисляется их сумма х+у
- 23. Если измеряются две величины х и у и вычисляется их произведение х·у или их частное х/у,
- 27. Измеряем толщину Т 100 листов бумаги и получаем результат
- 31. Независимые погрешности в сумме
- 40. тогда в соответствии с правилом погрешность равна
- 41. Степенная функция
- 52. Скачать презентацию

































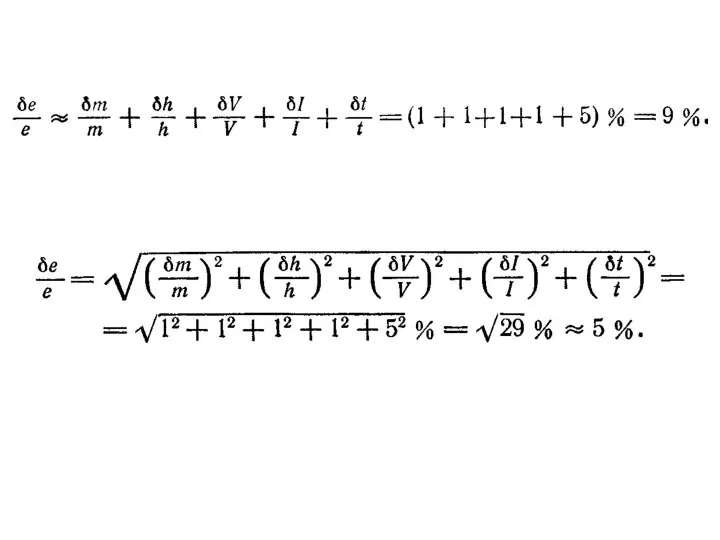






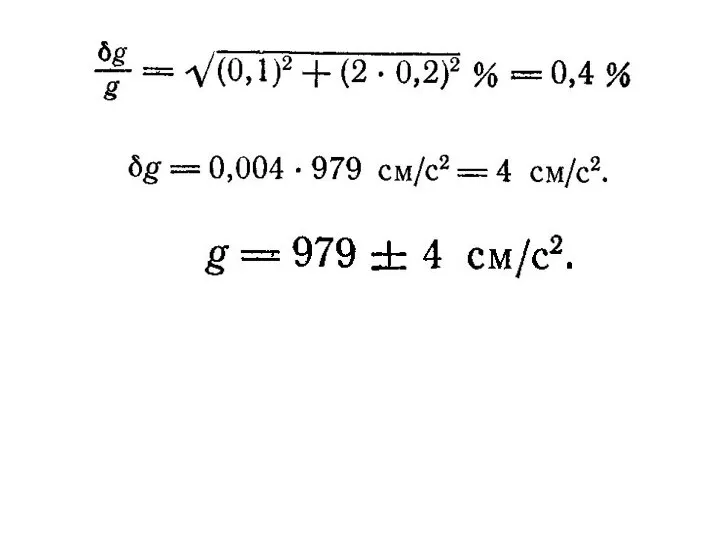

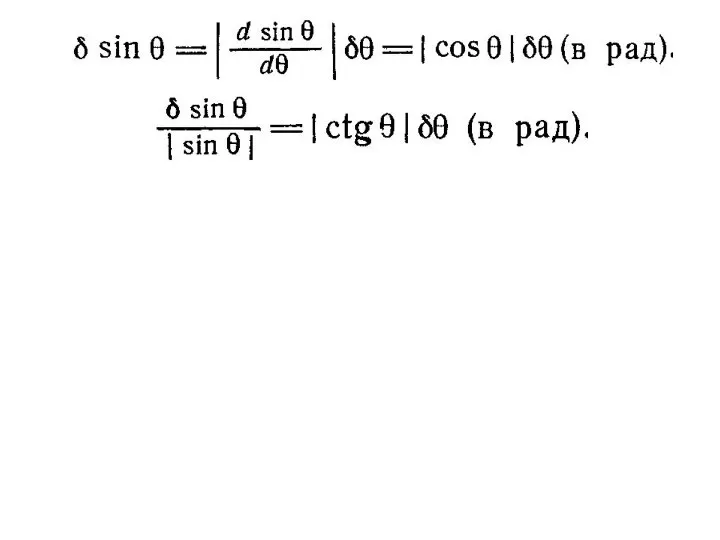



 Методы интегрирования
Методы интегрирования Понятие логарифма
Понятие логарифма Линейная алгебра. Применение определителей
Линейная алгебра. Применение определителей Линейные неравенства. Системы линейных неравенств. Повторение
Линейные неравенства. Системы линейных неравенств. Повторение Математическая статистика (среднее арифметическое, мода, размах, медиана) комбинаторика
Математическая статистика (среднее арифметическое, мода, размах, медиана) комбинаторика Четырёхугольники, их признаки и свойства. Геометрия. 8 класс
Четырёхугольники, их признаки и свойства. Геометрия. 8 класс Параллельность плоскостей определение
Параллельность плоскостей определение Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Непрерывные дроби
Непрерывные дроби Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Постороение графиков функций
Постороение графиков функций Углы
Углы Десятичные дроби Десятичная запись дробных чисел
Десятичные дроби Десятичная запись дробных чисел Наибольшее и наименьшее значения функции. Применение производной к исследованию функций
Наибольшее и наименьшее значения функции. Применение производной к исследованию функций Область определения выражения
Область определения выражения Многоугольники
Многоугольники «Роль игры в процессе обучения на уроках математики»
«Роль игры в процессе обучения на уроках математики» формулы сокращенного умножения
формулы сокращенного умножения Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов
Использование кватернионов в решении задачи навигации в трехмерном пространстве при помощи выделенных линейных объектов Комбинаторная задача с лампочками
Комбинаторная задача с лампочками Большие квадраты
Большие квадраты Один. Много
Один. Много Признаки делимости чисел
Признаки делимости чисел Параллельный перенос
Параллельный перенос Презентация на тему Тренажер по формулам сокращенного умножения
Презентация на тему Тренажер по формулам сокращенного умножения  Подготовка к ОГЭ по математике
Подготовка к ОГЭ по математике Формула Пика
Формула Пика Фракталы: Красота в простом
Фракталы: Красота в простом