Содержание
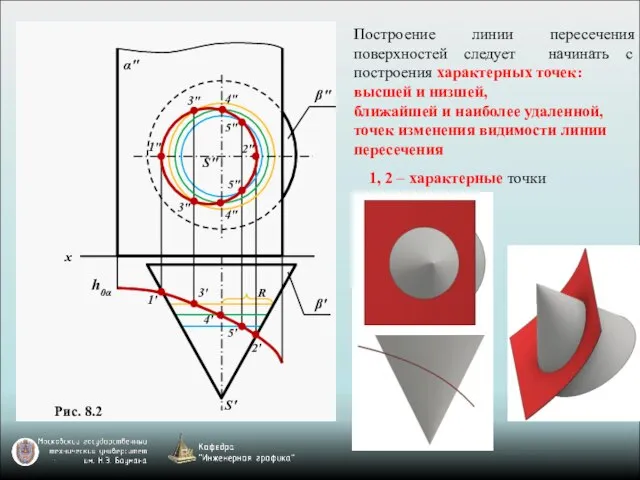
- 2. Построение линии пересечения поверхностей, одна их которых занимает проецирующее положение Линией пересечения двух поверхностей называется линия,
- 3. Рис. 8.2 2' 1' 4' 3' 5' S' β' h0α 3" 2" 1" 3" 4" 4"
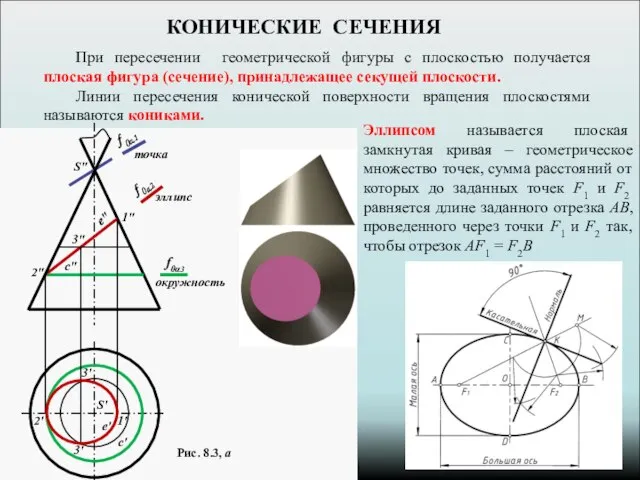
- 4. КОНИЧЕСКИЕ СЕЧЕНИЯ При пересечении геометрической фигуры с плоскостью получается плоская фигура (сечение), принадлежащее секущей плоскости. Линии
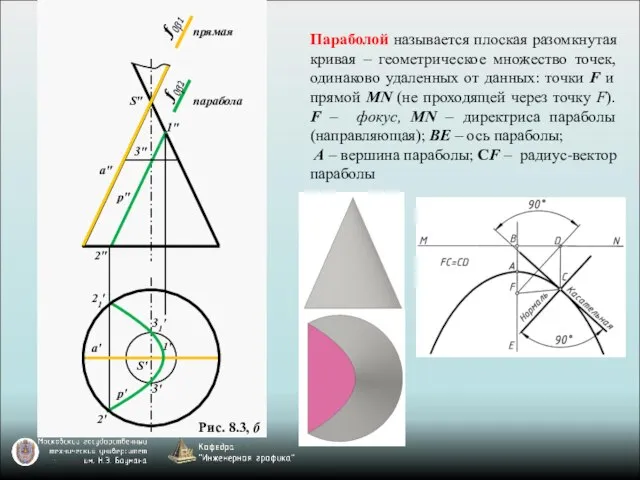
- 5. Рис. 8.3, б Параболой называется плоская разомкнутая кривая – геометрическое множество точек, одинаково удаленных от данных:
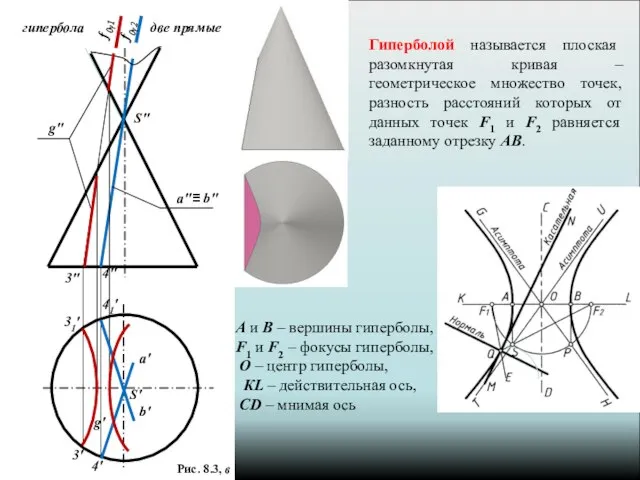
- 6. Рис. 8.3, в Гиперболой называется плоская разомкнутая кривая – геометрическое множество точек, разность расстояний которых от
- 7. Построение линии пересечения поверхностей общего положения Рис. 8.4 Алгоритм решения: Ввести вспомогательную поверхность-посредник ϒ1 Построить линии
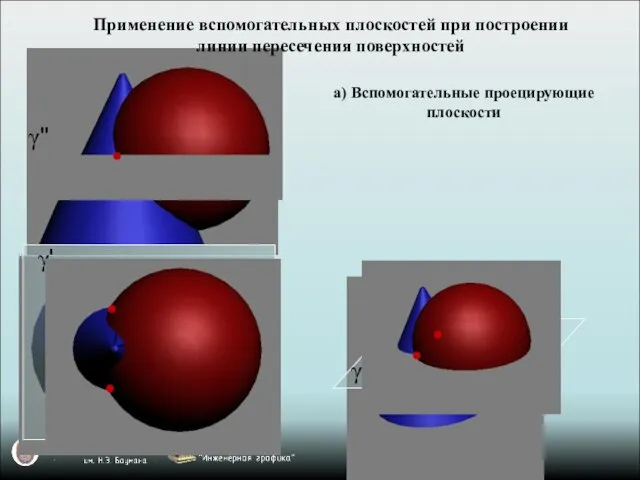
- 8. γ" γ' γ а) Вспомогательные проецирующие плоскости Применение вспомогательных плоскостей при построении линии пересечения поверхностей
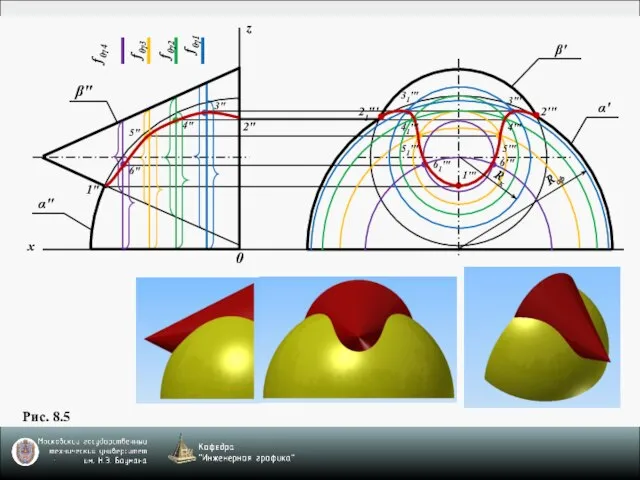
- 9. Рис. 8.5 f0γ1 f0γ2 f0γ3 f0γ4 z x 0 α" β" 1" 2" α' β' 2'"
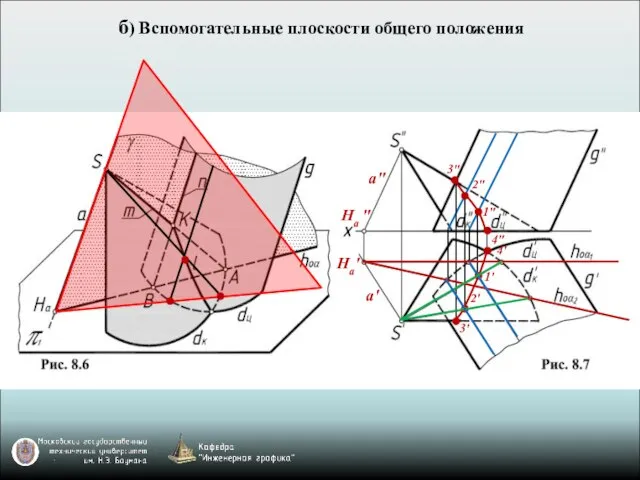
- 10. б) Вспомогательные плоскости общего положения 1' 2' 2" 1" 3' 3" 4' 4" a' Ha' a"
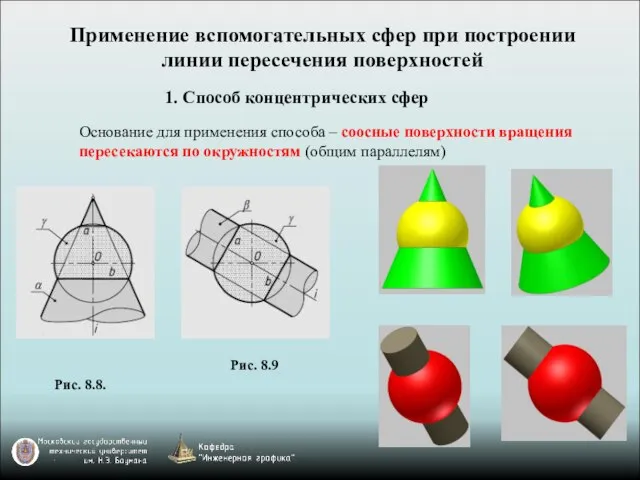
- 11. Применение вспомогательных сфер при построении линии пересечения поверхностей 1. Способ концентрических сфер Основание для применения способа
- 12. Область применения способа: Обе пересекающиеся поверхности – поверхности вращения Оси поверхностей вращения пересекаются Плоскость симметрии, определяемая
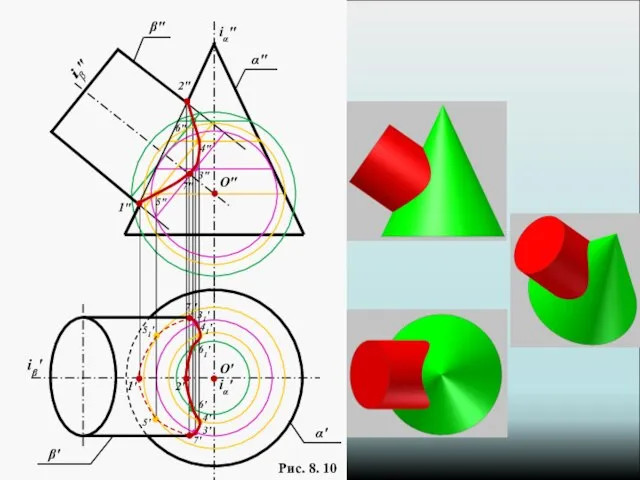
- 13. Рис. 8. 10 α" iα" β" iβ" O" 1" 2" Rmin Rmax O' 2' 1' β'
- 14. Рис. 8. 10 O" O' 1' 2' 71' 7' 2" 1" 7" β" α" iα" iβ"
- 15. 2. Способ эксцентрических сфер В основу способа положено обстоятельство, что одна и та же окружность с
- 16. Область применения способа: Одна из пересекающихся поверхностей – поверхность вращения, вторая поверхность содержит семейство круговых сечений
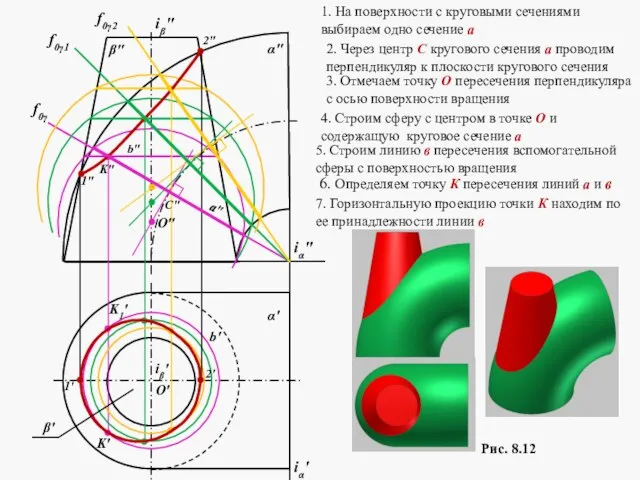
- 17. Алгоритм построения линии пересечения поверхностей, используя способ эскцентрических сфер: На поверхности с круговыми сечениями выбираем одно
- 18. Рис. 8.12 1" 2" f0γ a" C" O" b" K" K' K1' b' iβ' iα' 2'
- 19. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ Рис. 8.13 Конические поверхности с общей вершиной пересекаются по общим образующим Сумма
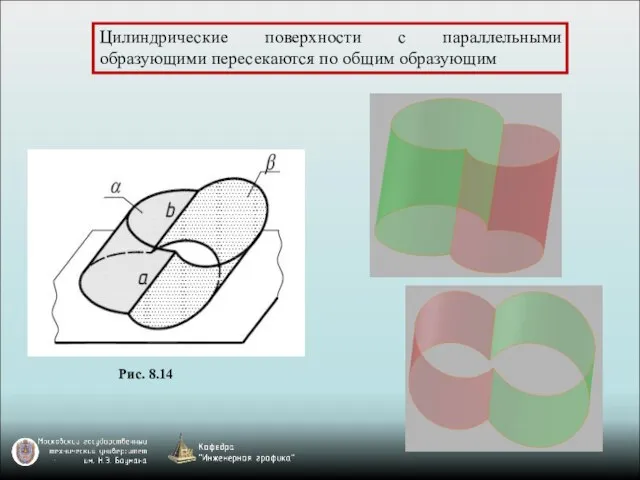
- 20. Цилиндрические поверхности с параллельными образующими пересекаются по общим образующим Рис. 8.14
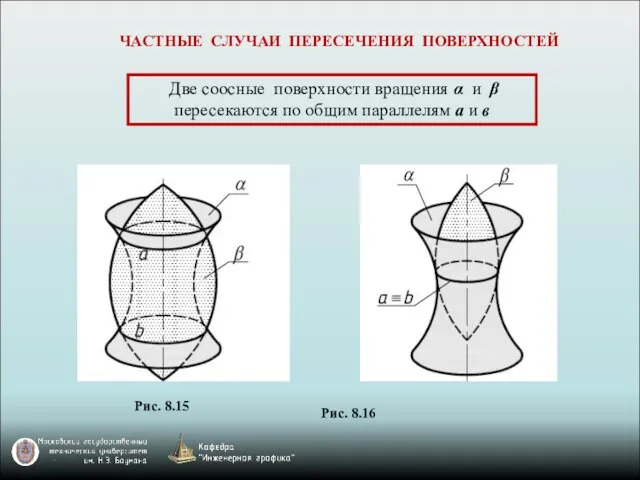
- 21. Две соосные поверхности вращения α и β пересекаются по общим параллелям а и в Рис. 8.16
- 22. ПОСТРОЕНИЕ ОЧЕРКА ПОВЕРХНОСТИ ВРАЩЕНИЯ Для построения очерковых образующих поверхности вращения с наклонной осью в нее вписывается
- 23. Рис. 8.18 Для построения поверхности конуса вращения с наклонной осью необходимо вписать в конус сферу и
- 24. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА Теорема. Если две поверхности второго порядка пересекаются по одной плоской
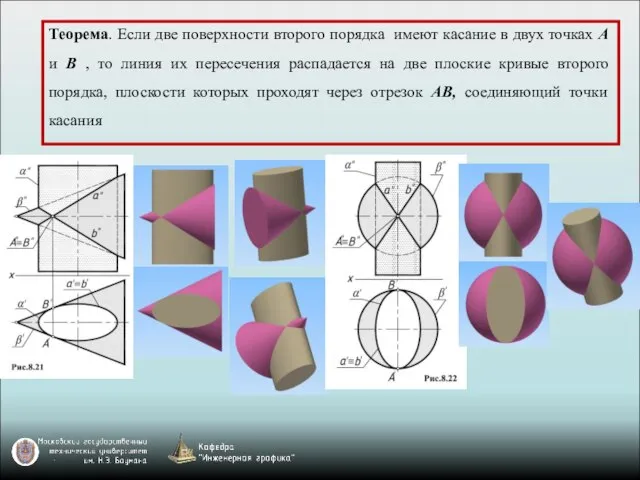
- 25. Теорема. Если две поверхности второго порядка имеют касание в двух точках А и В , то
- 26. Теорема Монжа Проекция линии касания (окружность) цилиндра и сферы Проекция линии касания (окружность) конуса и сферы
- 28. Скачать презентацию












 Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Письмо цифры 6
Письмо цифры 6 Задачи по геометрии
Задачи по геометрии Стереометрия. Геометрия
Стереометрия. Геометрия Открытое акционерное общество в 6 классе
Открытое акционерное общество в 6 классе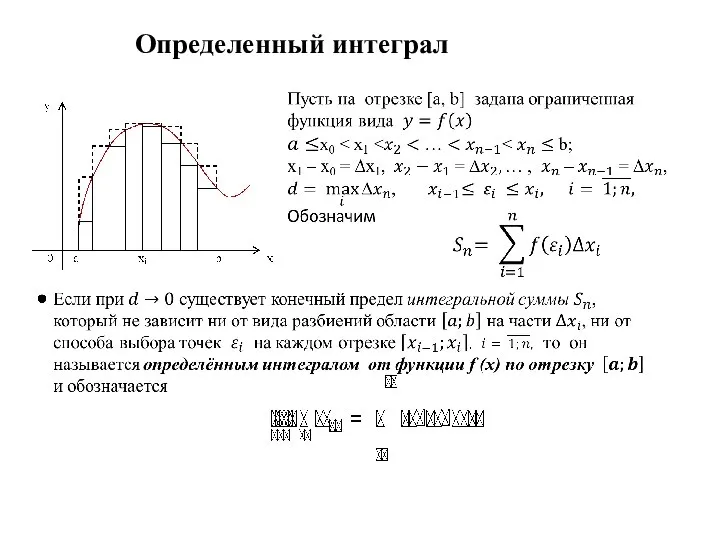 Определённый интеграл
Определённый интеграл Разметка прямоугольника по угольнику
Разметка прямоугольника по угольнику Суждение, как форма мышления. Классификация
Суждение, как форма мышления. Классификация Квадратичная функция
Квадратичная функция Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Урок-КВН
Урок-КВН Названия чисел в записях действий
Названия чисел в записях действий Подготовка к контрольной работе. Уравнения
Подготовка к контрольной работе. Уравнения Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5
Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5 Математическое обеспечение (МО) цифрового (автоматизированного) проектирования
Математическое обеспечение (МО) цифрового (автоматизированного) проектирования Площади фигур
Площади фигур Какие бывают графы
Какие бывают графы Понятие цилиндра
Понятие цилиндра Степенная функция и её график
Степенная функция и её график Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Задачи для подготовки к контрольной работе
Задачи для подготовки к контрольной работе Решение треугольников
Решение треугольников Устный счёт. Назови числа по порядку
Устный счёт. Назови числа по порядку Entrant
Entrant Угол между векторами (часть 2)
Угол между векторами (часть 2) Сложение +5
Сложение +5 Формирование алгоритмического мышления у младших школьников
Формирование алгоритмического мышления у младших школьников Презентация на тему Величины (4 класс)
Презентация на тему Величины (4 класс)