Изучить понятия параллельное проектирование и его

1. Изучить понятия «параллельное проектирование» и его свойства, продолжить формирование навыков работы с чертежными инструментами, в частности, построение изображений пересекающихся, параллельных и скрещивающихся прямых;
2. Продолжить развития абстрактного мышления, пространственного воображения, познавательного интереса.
задачи урока :

В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно для этого используется параллельное проектирование пространственной фигуры на плоскость.

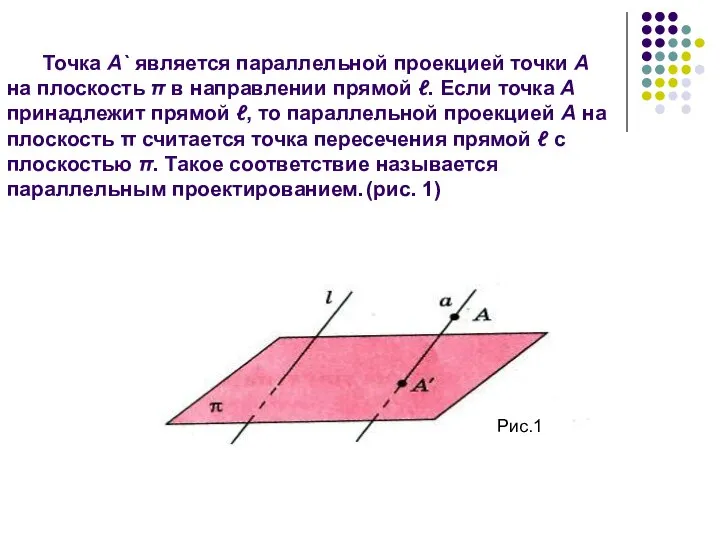
Точка А` является параллельной проекцией точки А на плоскость π в направлении прямой ℓ. Если точка А принадлежит прямой ℓ, то параллельной проекцией А на плоскость π считается точка пересечения прямой ℓ с плоскостью π. Такое соответствие называется параллельным проектированием. (рис. 1)

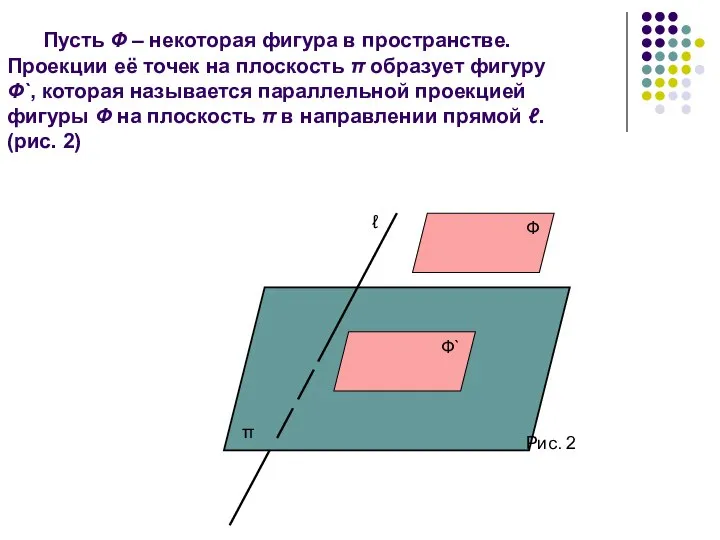
Пусть Ф – некоторая фигура в пространстве. Проекции её точек на плоскость π образует фигуру Ф`, которая называется параллельной проекцией фигуры Ф на плоскость π в направлении прямой ℓ. (рис. 2)

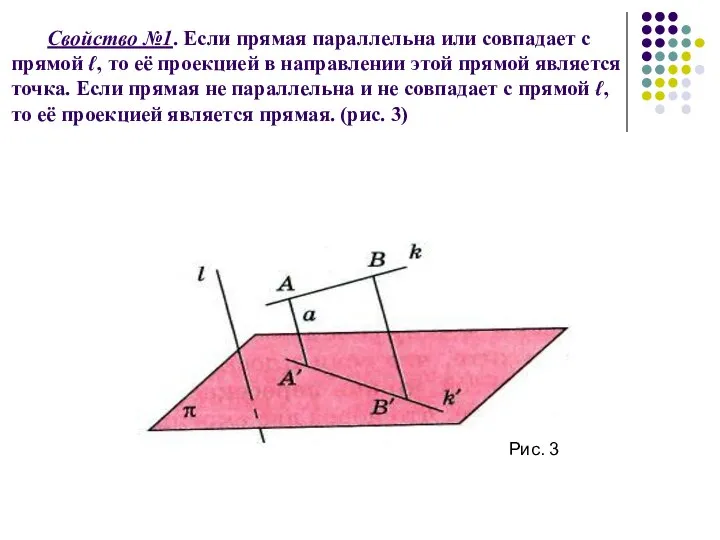
Свойство №1. Если прямая параллельна или совпадает с прямой ℓ, то её проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой ℓ, то её проекцией является прямая. (рис. 3)

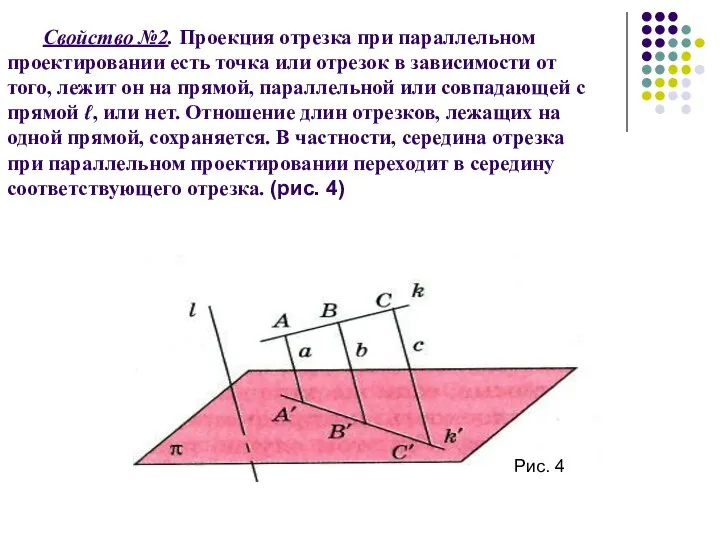
Свойство №2. Проекция отрезка при параллельном проектировании есть точка или отрезок в зависимости от того, лежит он на прямой, параллельной или совпадающей с прямой ℓ, или нет. Отношение длин отрезков, лежащих на одной прямой, сохраняется. В частности, середина отрезка при параллельном проектировании переходит в середину соответствующего отрезка. (рис. 4)

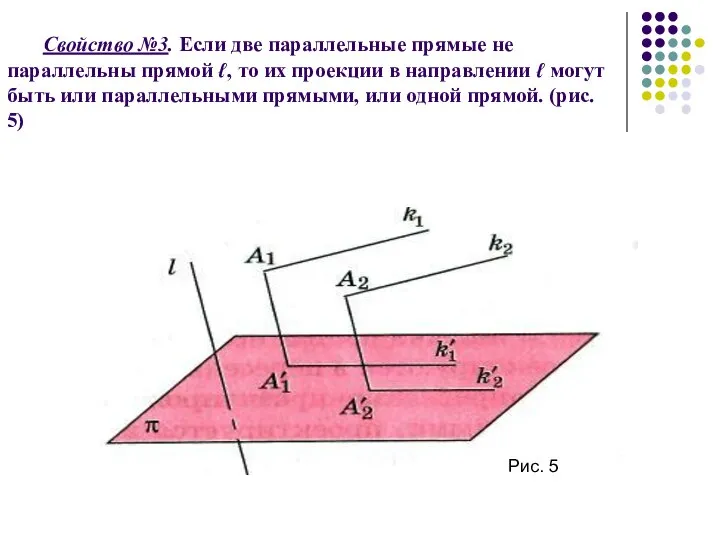
Свойство №3. Если две параллельные прямые не параллельны прямой ℓ, то их проекции в направлении ℓ могут быть или параллельными прямыми, или одной прямой. (рис. 5)

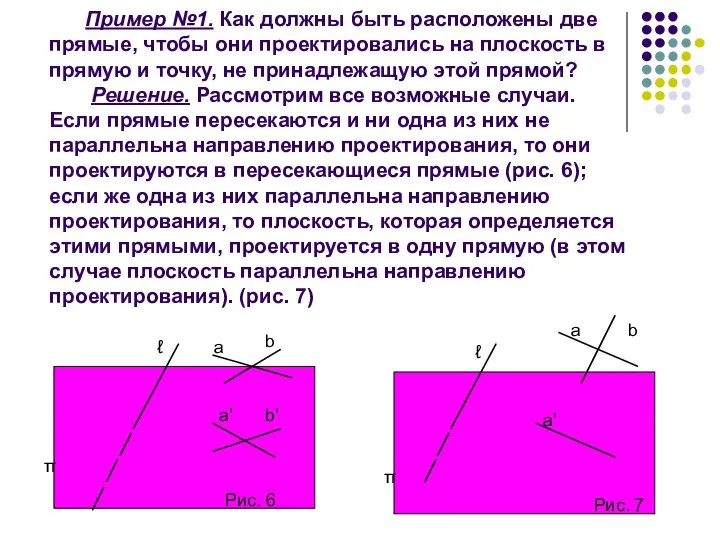
Пример №1. Как должны быть расположены две прямые, чтобы они проектировались на плоскость в прямую и точку, не принадлежащую этой прямой? Решение. Рассмотрим все возможные случаи. Если прямые пересекаются и ни одна из них не параллельна направлению проектирования, то они проектируются в пересекающиеся прямые (рис. 6); если же одна из них параллельна направлению проектирования, то плоскость, которая определяется этими прямыми, проектируется в одну прямую (в этом случае плоскость параллельна направлению проектирования). (рис. 7)

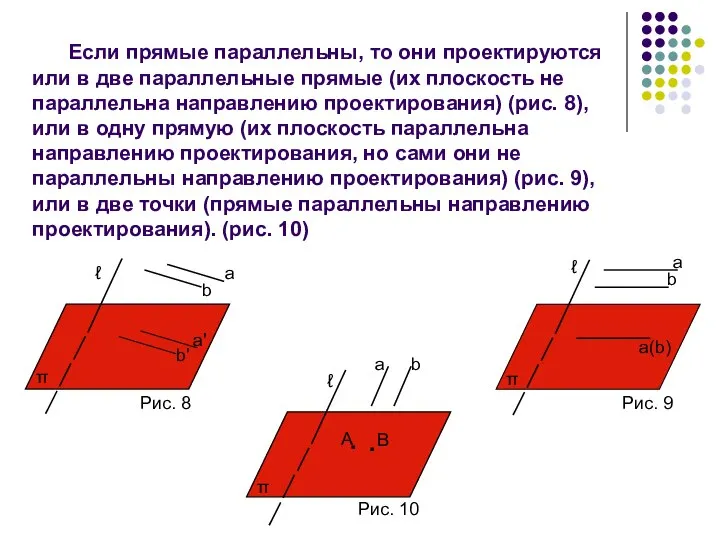
Если прямые параллельны, то они проектируются или в две параллельные прямые (их плоскость не параллельна направлению проектирования) (рис. 8), или в одну прямую (их плоскость параллельна направлению проектирования, но сами они не параллельны направлению проектирования) (рис. 9), или в две точки (прямые параллельны направлению проектирования). (рис. 10)

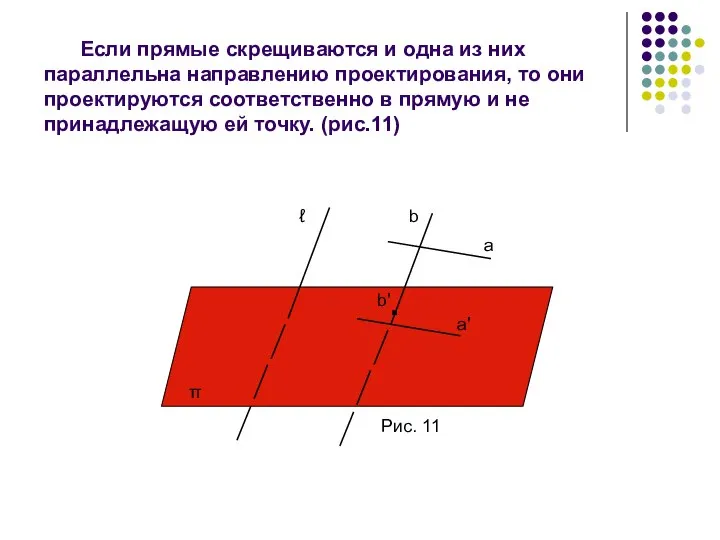
Если прямые скрещиваются и одна из них параллельна направлению проектирования, то они проектируются соответственно в прямую и не принадлежащую ей точку. (рис.11)

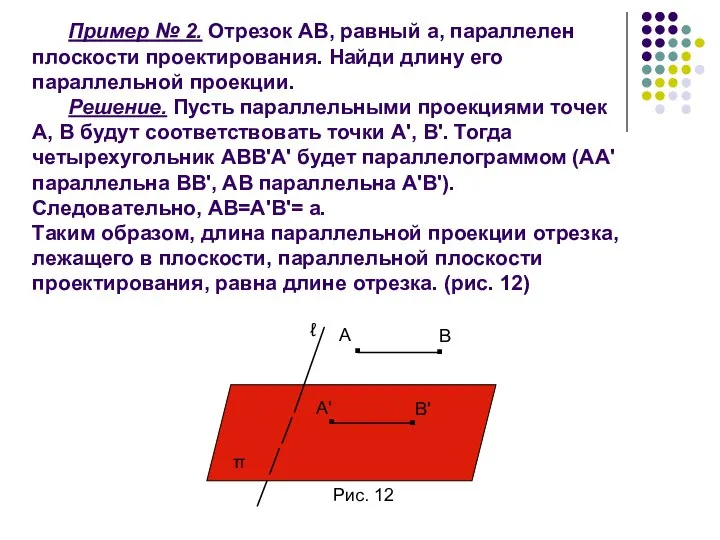
Пример № 2. Отрезок АВ, равный а, параллелен плоскости проектирования. Найди длину его параллельной проекции.
Решение. Пусть параллельными проекциями точек А, В будут соответствовать точки А', В'. Тогда четырехугольник АВВ'А' будет параллелограммом (АА' параллельна ВВ', АВ параллельна А'В'). Следовательно, АВ=А'В'= а.
Таким образом, длина параллельной проекции отрезка, лежащего в плоскости, параллельной плоскости проектирования, равна длине отрезка. (рис. 12)

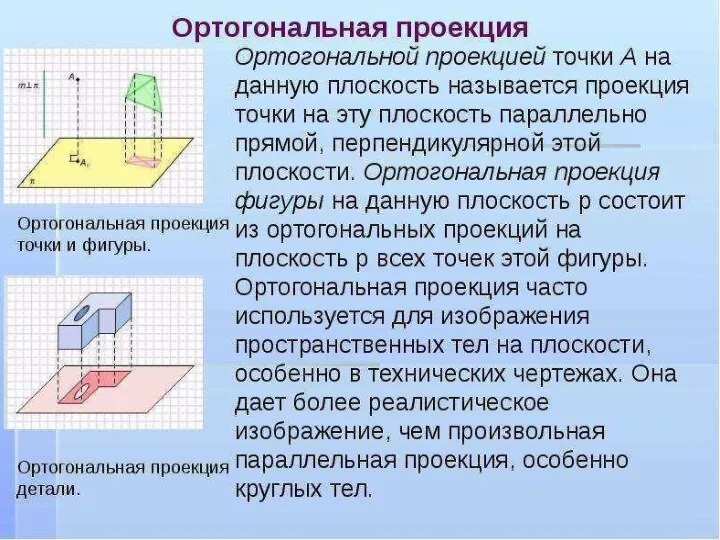
Ортогональное проектирование
Ортогональное проектирование является частным случаем параллельного проектирования. Ортогональное проектирование - это такое параллельное проектирование, при котором прямая проектирования перпендикулярна плоскости проекции.