Содержание
- 2. Определение производной функции? Производной функции в данной точке называется предел отношения приращения функции в этой точке
- 3. Устная работа 1 сosх sinх+12
- 4. Устная работа
- 5. Используя определение производной функции, решают ряд задач в алгебре, физике, химии. Рассмотрим физический смысл производной. материальная
- 6. Задача: Точка движется прямолинейно по закону s(t) = t3+ 2t ( где s(t) – измеряется в
- 7. Что мы сделали за часть урока? Повторили определение производной функции и формулы дифференцирования. Решили задачу на
- 8. Задача: По прямой движется материальная точка, скорость которой в момент времени t задается формулой v(t) =
- 9. При решении задачи, мы, зная производную функции, восстановили ее первичный образ. Эта операция восстановления - операция
- 10. y = F(x) называют первообразной для y = f(x) на промежутке X, если при x ∈
- 11. Операция дифферен-цирования функция y = F(х) (первообразная) y = f(х) производная Операция интегри- рования В математике
- 12. Запомните: Первообразная – это родитель производной:
- 13. Задача: Найдите все первообразные для функций: f(х)=3 f(х)= х2 f(х)=cosx f(х)=12 f(х)=х5
- 14. Три правила нахождения первообразных Если функции у=f(x) и у=g(x) имеют на промежутке первообразные соответственно у=F(x) и
- 15. Найти первообразные для функции Решение: Используя правила нахождения первообразных и таблицу получим
- 18. Скачать презентацию















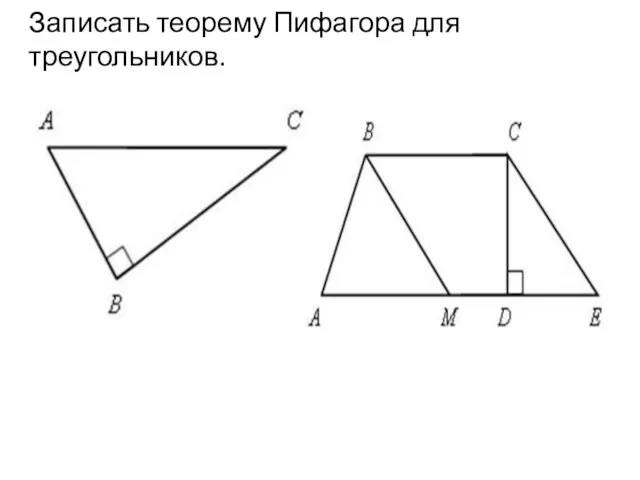 Теорема Пифагора. Урок 24
Теорема Пифагора. Урок 24 Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Можно ли измерить длину окружности?
Можно ли измерить длину окружности? Умножение многочлена на многочлен
Умножение многочлена на многочлен Элементы теории графов
Элементы теории графов Математическая логика
Математическая логика Площадь круга и его частей
Площадь круга и его частей Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Метрология. Погрешность измерений
Метрология. Погрешность измерений Математический маятник. Измерения
Математический маятник. Измерения Презентация на тему Функция
Презентация на тему Функция  Решение примеров на сложение в пределах 20. (1-2 класс)
Решение примеров на сложение в пределах 20. (1-2 класс) Теория вероятностей
Теория вероятностей Действия с десятичными дробями
Действия с десятичными дробями Круглые числа. Величина
Круглые числа. Величина Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц
Графическая лаборатория Цель: систематизировать знания по теме «Функции и их графики», закрепить навыки работы с графиками функц Математический проект
Математический проект Случаи вычитания
Случаи вычитания Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Волшебные палочки. Головоломки
Волшебные палочки. Головоломки Перемещение тела на плоскости (задача)
Перемещение тела на плоскости (задача) объём DVD диска
объём DVD диска Линейные неравенства с параметром
Линейные неравенства с параметром Порядковый счёт в пределах 10
Порядковый счёт в пределах 10 Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Тригонометрия. Восхождение на пик
Тригонометрия. Восхождение на пик Красота многогранников и не только. Из природы в науку
Красота многогранников и не только. Из природы в науку