Содержание
- 2. Сложение в десятичной системе.
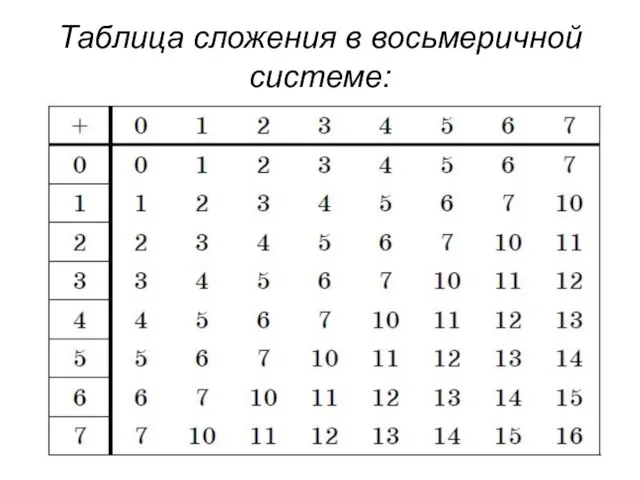
- 3. Таблица сложения в восьмеричной системе:
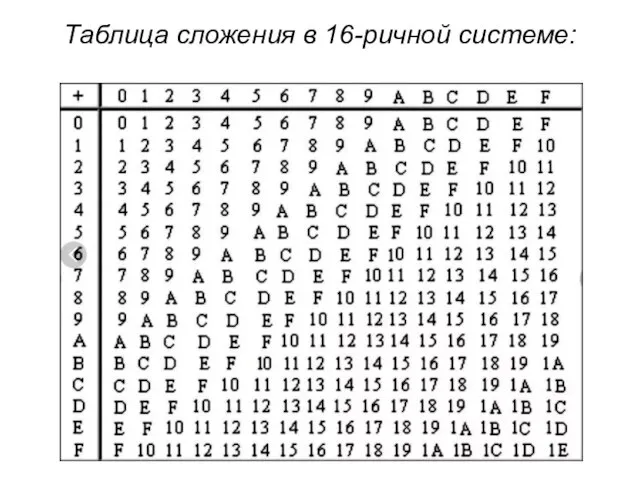
- 4. Таблица сложения в 16-ричной системе:
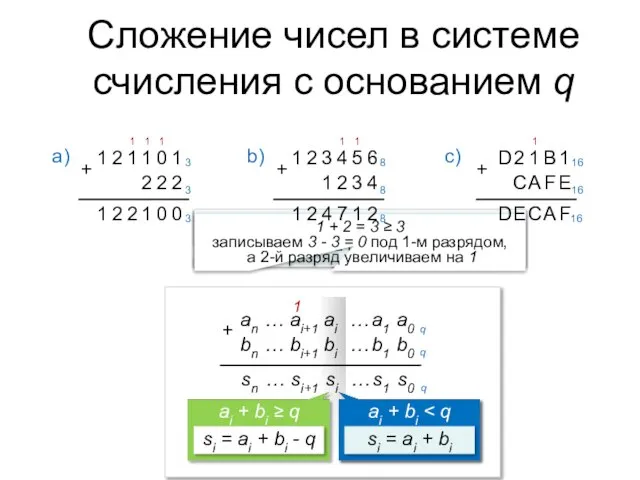
- 5. Правило сложения Aq+Bq=S Чтобы в системе счисления с снованием q получить сумму S двух чисел A
- 6. 1 + 2 = 3 ≥ 3 записываем 3 – 3 = 0 под 2-м разрядом,
- 7. Сложение чисел с разным основанием Для того, чтобы сложить два числа с разными основаниями систем счисления,
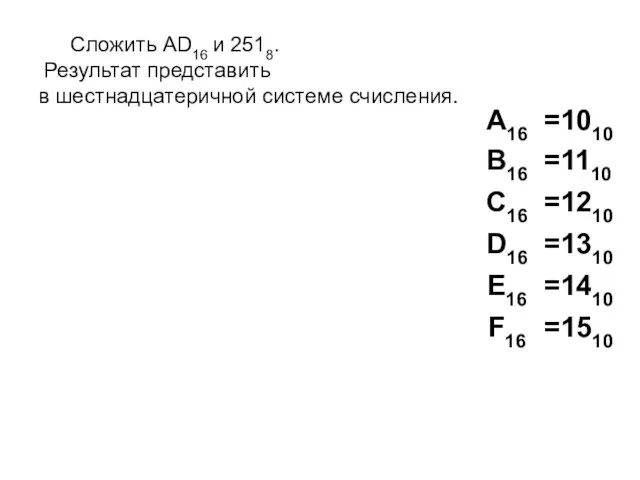
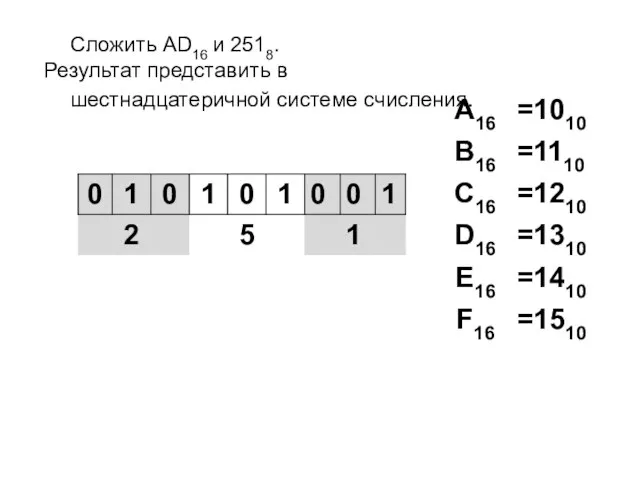
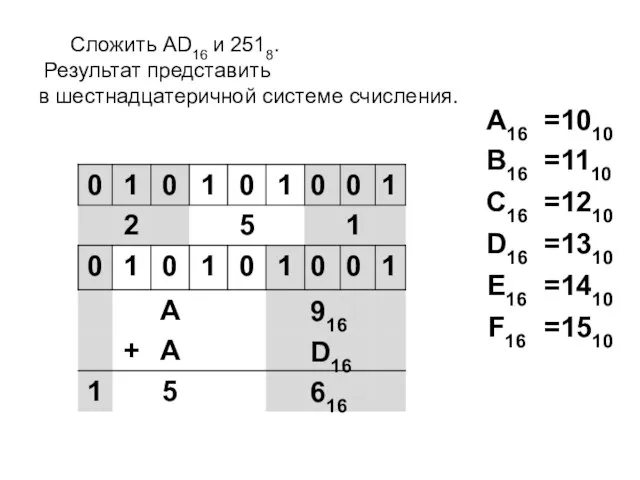
- 8. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
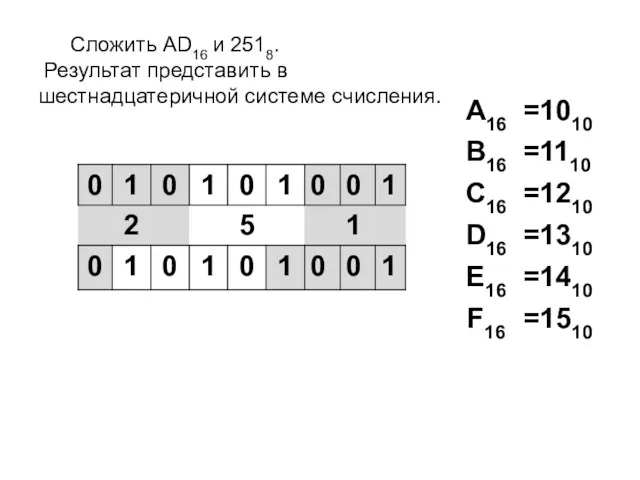
- 9. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
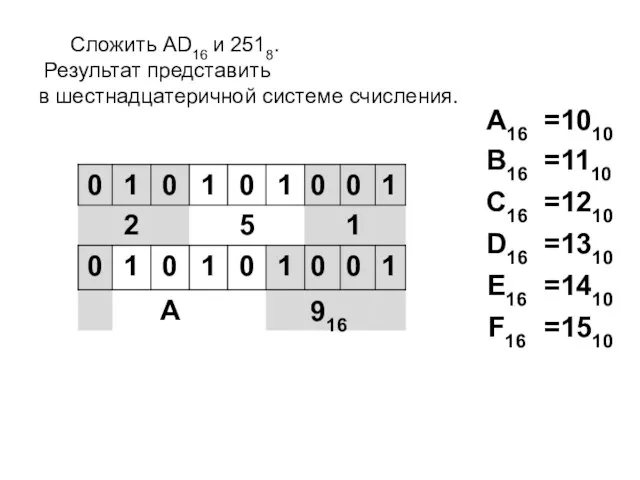
- 10. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
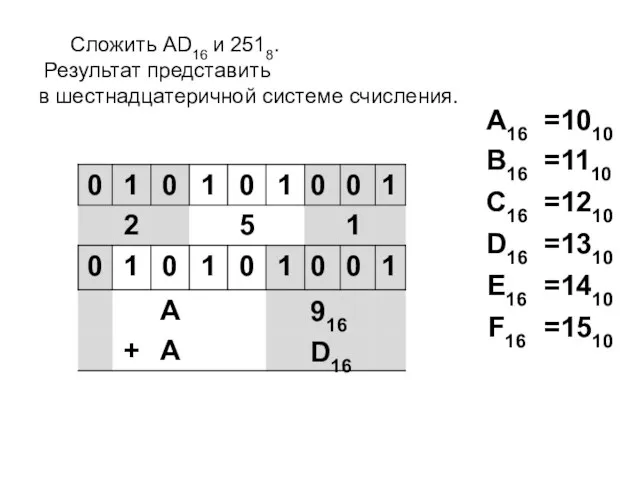
- 11. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
- 12. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
- 13. Сложить AD16 и 2518. Результат представить в шестнадцатеричной системе счисления.
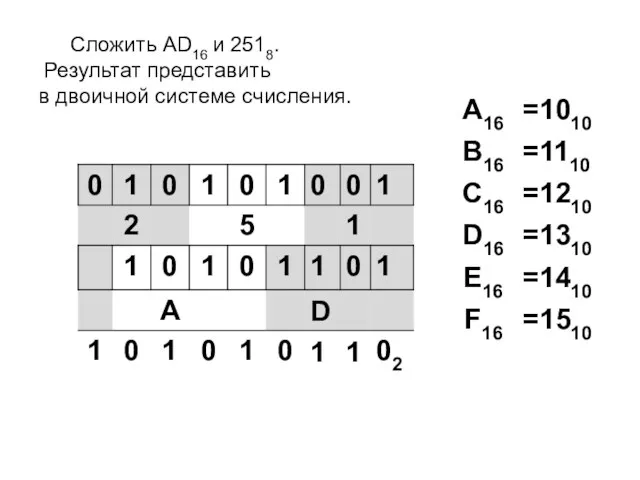
- 14. Сложить AD16 и 2518. Результат представить в двоичной системе счисления.
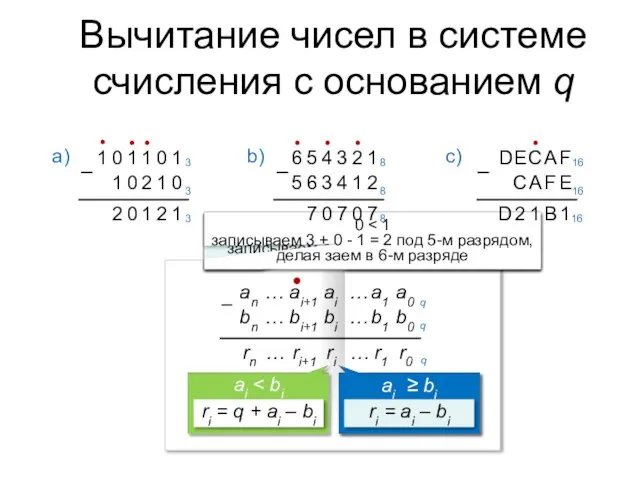
- 15. Правило вычитания Чтобы в системе счисления с основанием q получить разность R двух чисел A и
- 16. 0 = 0 записываем 0 под 4-м разрядом 0 0 1 ≥ 0 записываем 1 -
- 17. Правило вычитания чисел в системе счисления с основанием p Записать цифры числа друг под другом, соблюдая
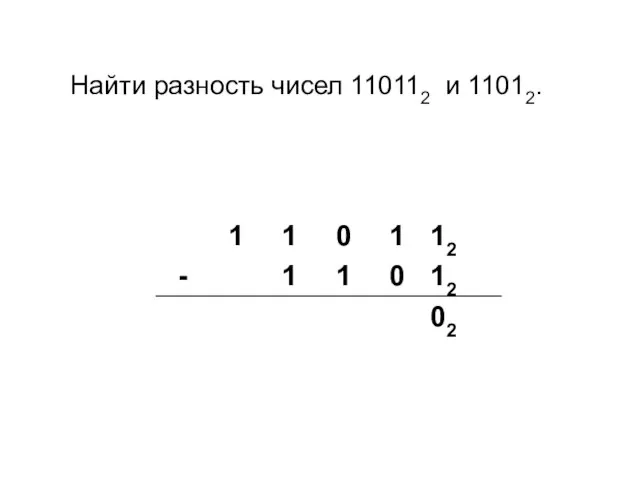
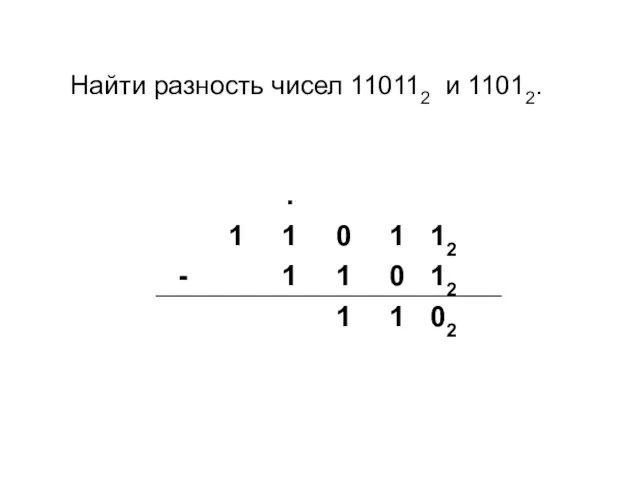
- 18. Найти разность чисел 110112 и 11012.
- 19. Найти разность чисел 110112 и 11012.
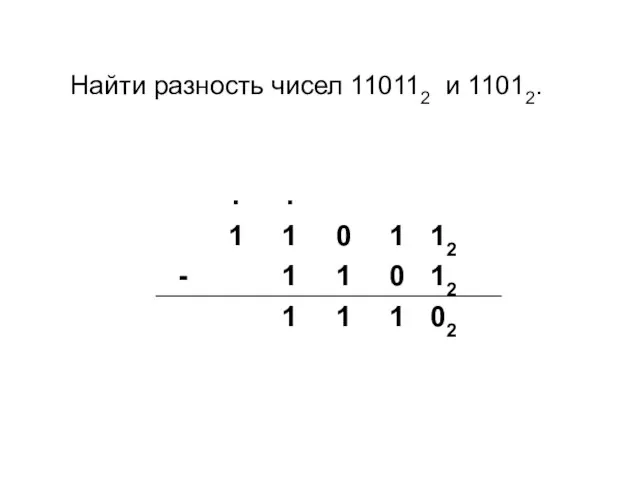
- 20. Найти разность чисел 110112 и 11012.
- 21. Найти разность чисел 110112 и 11012.
- 22. Найти разность чисел 110112 и 11012.
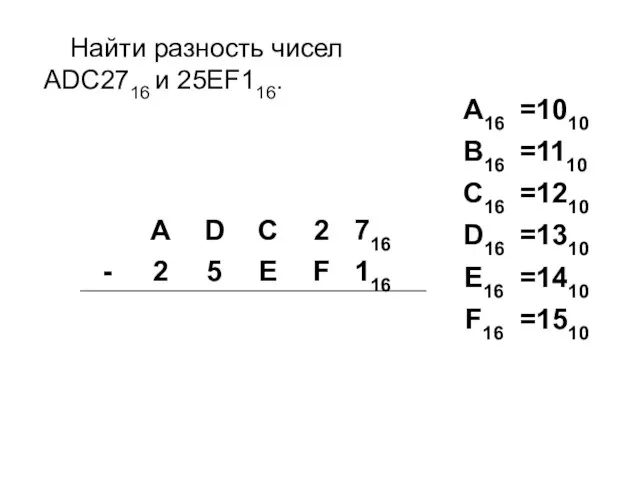
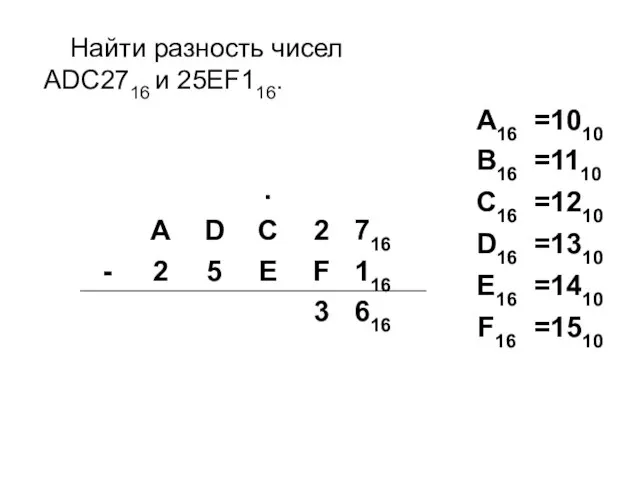
- 23. Найти разность чисел ADC2716 и 25EF116.
- 24. Найти разность чисел ADC2716 и 25EF116.
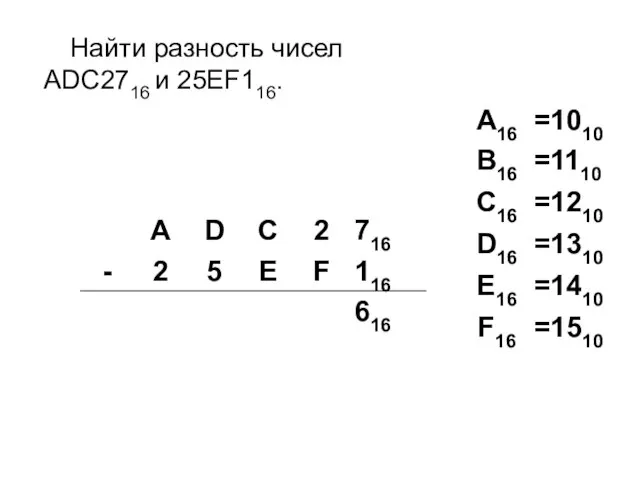
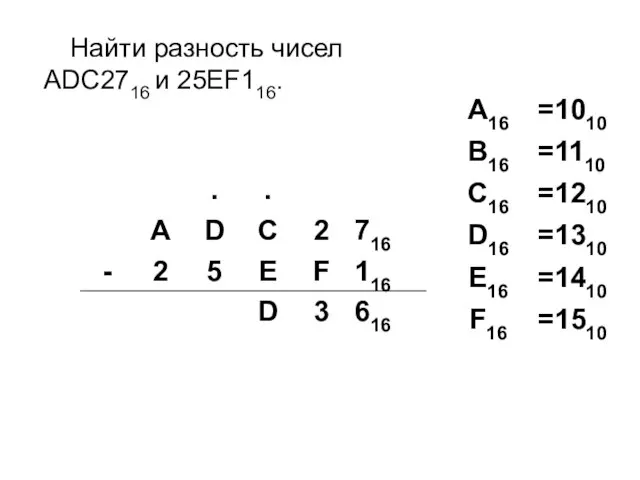
- 25. Найти разность чисел ADC2716 и 25EF116.
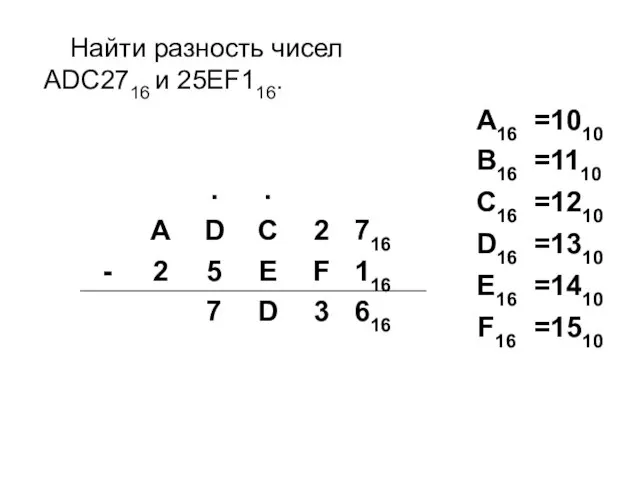
- 26. Найти разность чисел ADC2716 и 25EF116.
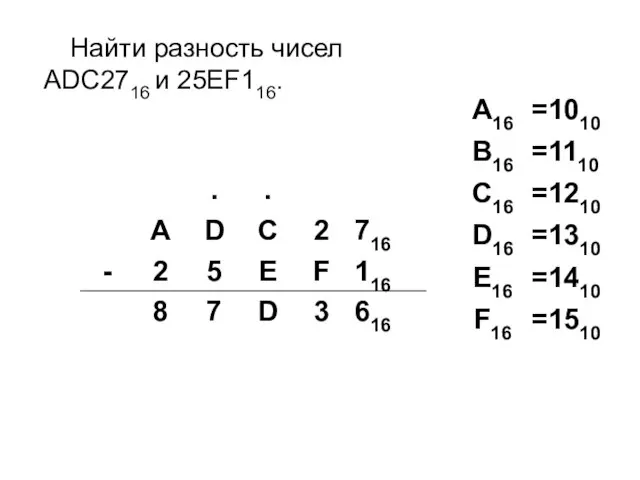
- 27. Найти разность чисел ADC2716 и 25EF116.
- 28. Найти разность чисел ADC2716 и 25EF116.
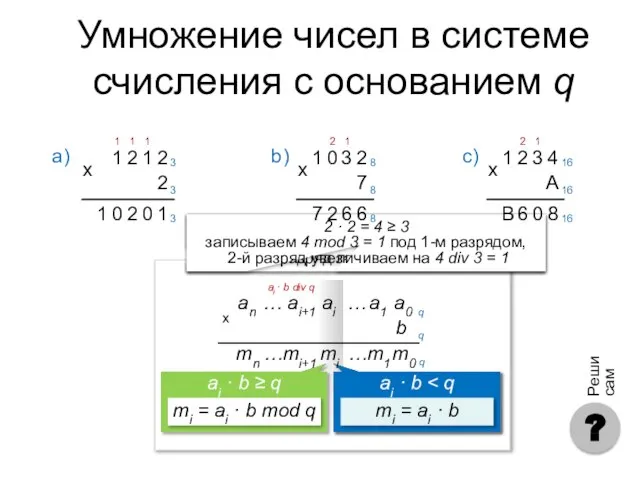
- 29. Правило умножения Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа
- 30. Div – деление нацело (остаток отбрасывается). Mod – остаток от деления. Примеры: 45 div 10 =
- 31. 1 · 2 + 1 = 3 ≥ 3 записываем 3 mod 3 = 0 под
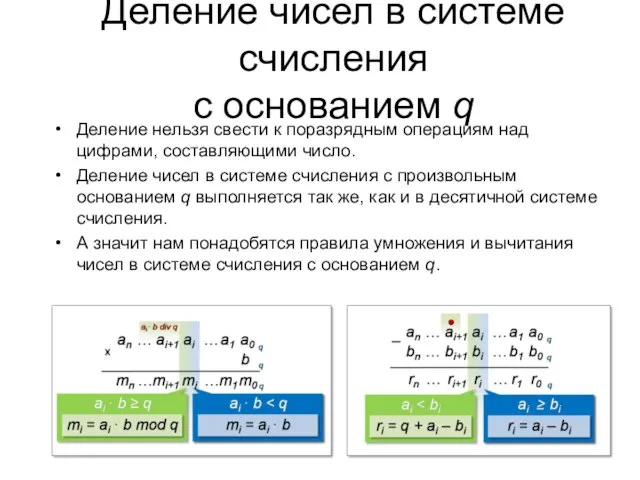
- 32. Деление нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с
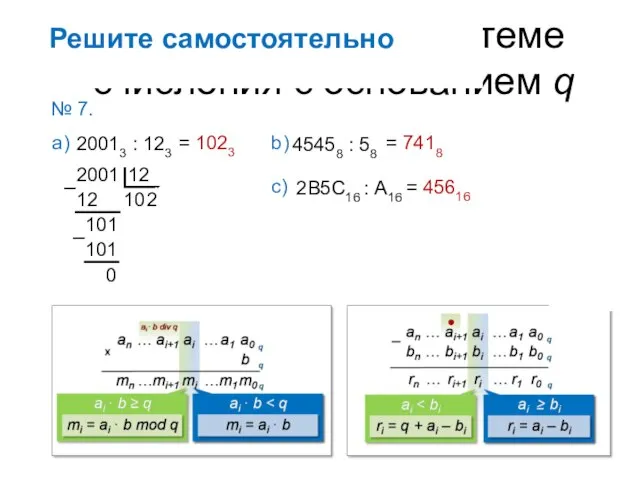
- 33. Деление чисел в системе счисления с основанием q а) ? Реши сам № 7. Решите самостоятельно
- 34. Задание Чему равна сумма чисел X= 438 и Y=568? Чему равна сумма чисел X= 4316 и
- 36. Скачать презентацию










 Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс
Презентация на тему Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс  Степенная функция
Степенная функция Числа. Комплексные числа
Числа. Комплексные числа Параллелограмм и его свойства и признаки
Параллелограмм и его свойства и признаки Тригонометрические формулы суммы и разности углов
Тригонометрические формулы суммы и разности углов Метод моментов решений различных классов дифференицальных и интегральных уравнений
Метод моментов решений различных классов дифференицальных и интегральных уравнений Задачи на части
Задачи на части Конкурс интерактивных презентаций Интерактивная мозаика“. Номинация Интерактивный тренажер
Конкурс интерактивных презентаций Интерактивная мозаика“. Номинация Интерактивный тренажер Презентация на тему Наука и образование в Древней Греции
Презентация на тему Наука и образование в Древней Греции  Методы оценки рисков
Методы оценки рисков Задачі без початкових умов
Задачі без початкових умов Уравнение Бернулли
Уравнение Бернулли Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Неравенство треугольника
Неравенство треугольника Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом
Разностные методы решения задач математической физики. Построение разностных схем интегро-интерполяционным методом Эконометрика
Эконометрика kg_1_prosteyshie_mat_operatsii
kg_1_prosteyshie_mat_operatsii Решение систем линейных неравенств
Решение систем линейных неравенств Решение задач по теме Признаки равенства треугольников
Решение задач по теме Признаки равенства треугольников Презентация на тему Подготовка к ГИА 2013
Презентация на тему Подготовка к ГИА 2013  Модели скоростей при движении по реке. 5 класс
Модели скоростей при движении по реке. 5 класс Презентация на тему Наибольший общий делитель, наименьшее общее кратное
Презентация на тему Наибольший общий делитель, наименьшее общее кратное  Правильные многогранники в философской картине мира Платона
Правильные многогранники в философской картине мира Платона Четырехугольники. Параллелограмм
Четырехугольники. Параллелограмм Концентрация кислоты
Концентрация кислоты Занимательная математика. 1 класс
Занимательная математика. 1 класс Таблица умножения
Таблица умножения Двойные интегралы в прямоугольной области
Двойные интегралы в прямоугольной области