Содержание
- 2. Конические сечения - это плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через
- 3. Конические сечения встречаются в природе и графически описывают многие физические процессы (закон Ома и закон Бойля-Мариотта),
- 4. 1)если секущая плоскость параллельна одной из образующих, то получается парабола; 2)если плоскость пересекает коническую поверхность по
- 6. Скачать презентацию



 Решение задач по теме Теорема Пифагора
Решение задач по теме Теорема Пифагора Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Путь и перемещение
Путь и перемещение Основные сведения о матрицах. Операции над матрицами
Основные сведения о матрицах. Операции над матрицами Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах
Элементы нелинейного функционального анализа Глава 1. Дифференциальное исчисление в нормированных пространствах Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3
Решение неравенств. Элективный курс. Алгебра 11 класс. Урок 3 Делители числа
Делители числа Золотое сечение
Золотое сечение Найдите производную функции. Практическая работа
Найдите производную функции. Практическая работа Число Пи
Число Пи Движение
Движение Способ группировки
Способ группировки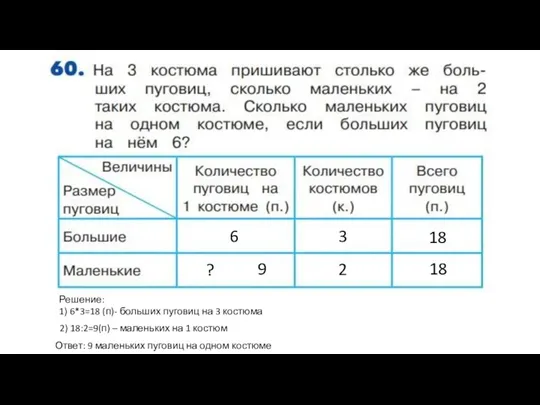 Задача о костюмах
Задача о костюмах Л11 Производная функции
Л11 Производная функции Задачи. Самостоятельная работа
Задачи. Самостоятельная работа Частное целых чисел. 6 класс
Частное целых чисел. 6 класс Исчисление высказываний
Исчисление высказываний Сложение чисел с переходом через десяток в пределах 20
Сложение чисел с переходом через десяток в пределах 20 Функции многих переменных: частные производные, дифференциалы. Лекция 2
Функции многих переменных: частные производные, дифференциалы. Лекция 2 Умножение одночлена на многочлен
Умножение одночлена на многочлен Площади поверхностей и объёмы тел вращения
Площади поверхностей и объёмы тел вращения Октаэдр
Октаэдр В мире цветов и плодов. Интегрированный урок биологии и математики
В мире цветов и плодов. Интегрированный урок биологии и математики Золотой треугольник и много интересного
Золотой треугольник и много интересного Презентация на тему Масштаб и его практическое применение
Презентация на тему Масштаб и его практическое применение 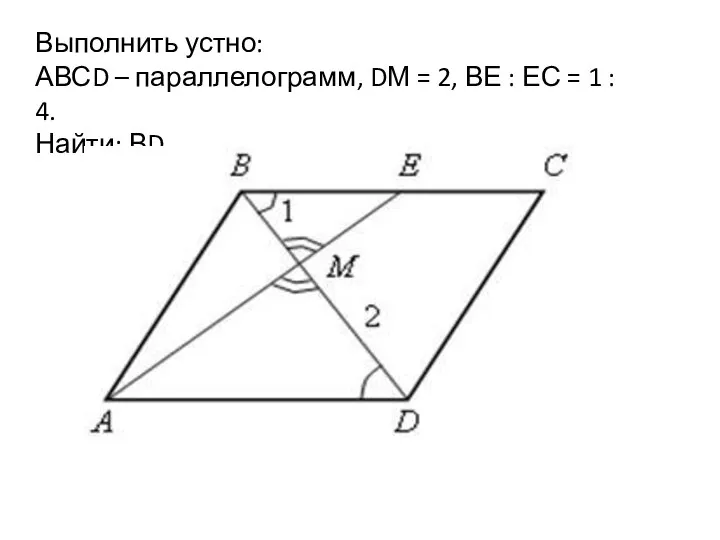 Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Симетричні фігури
Симетричні фігури Математические головоломки и игры
Математические головоломки и игры