Содержание
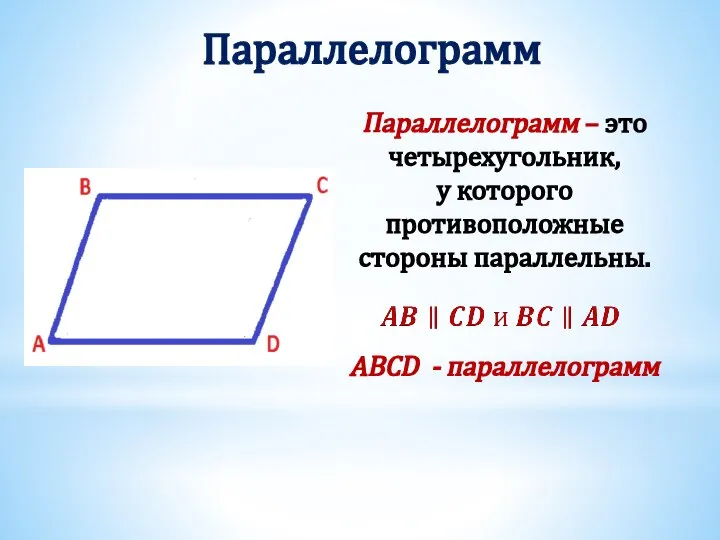
- 2. Параллелограмм ABCD - параллелограмм
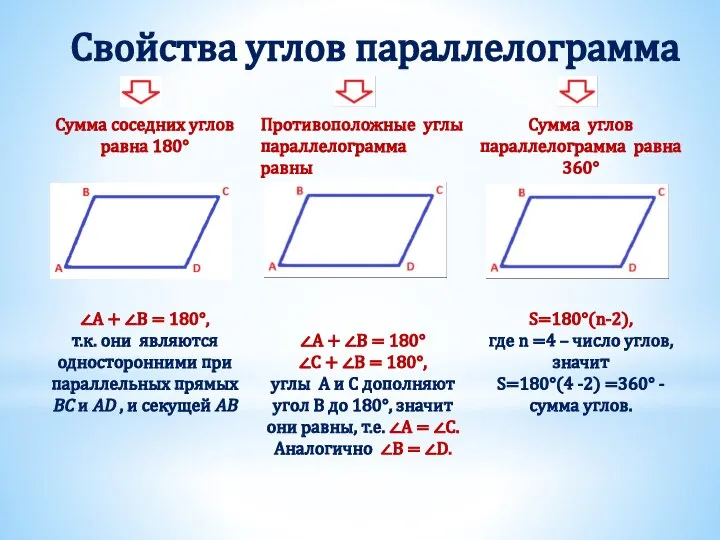
- 3. Свойства углов параллелограмма
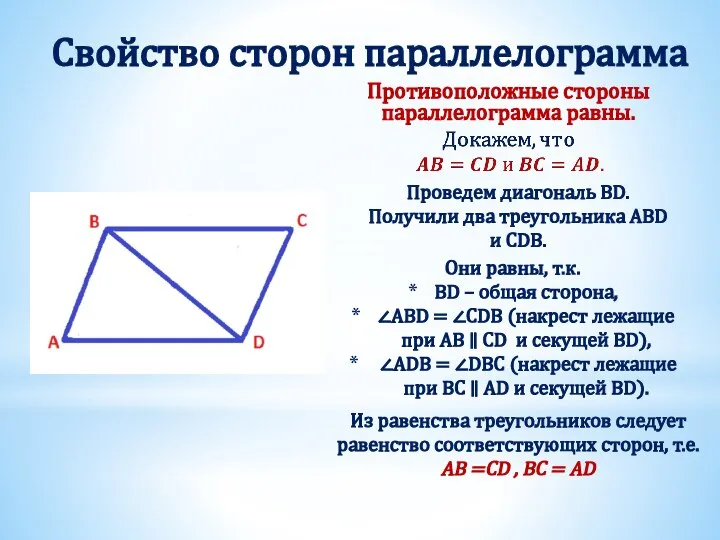
- 4. Свойство сторон параллелограмма Противоположные стороны параллелограмма равны. Проведем диагональ BD. Получили два треугольника АВD и СDB.
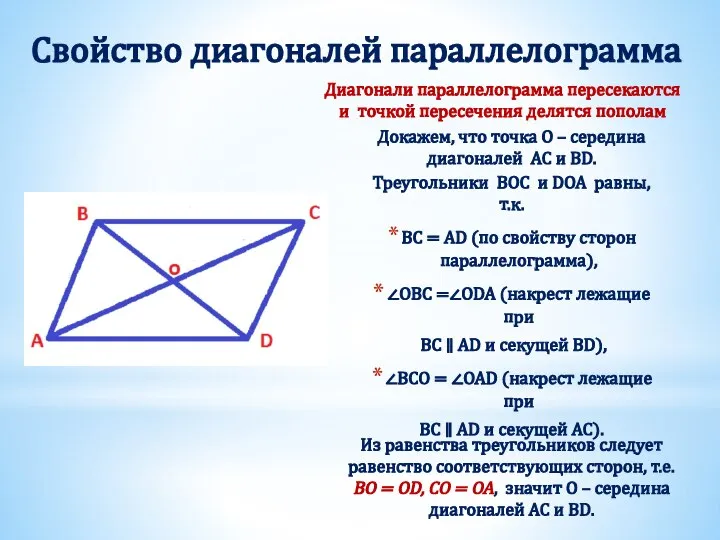
- 5. Свойство диагоналей параллелограмма Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам Докажем, что точка О –
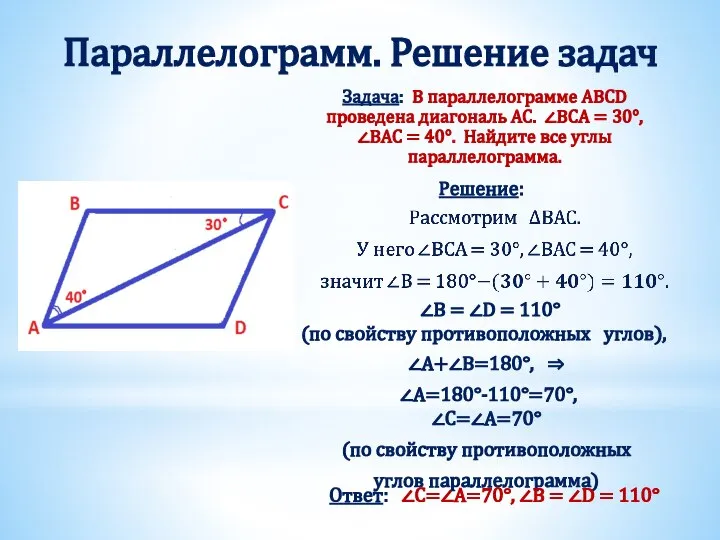
- 6. Параллелограмм. Решение задач Задача: В параллелограмме ABCD проведена диагональ AC. ∠BCA = 30°, ∠BAC = 40°.
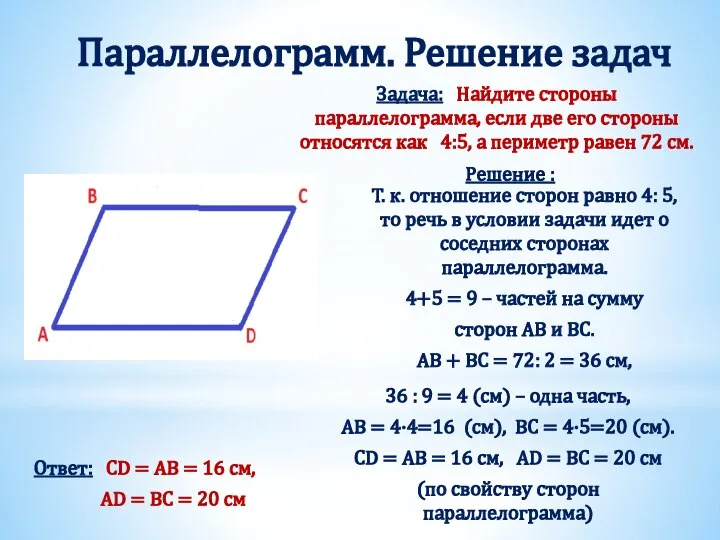
- 7. Параллелограмм. Решение задач Задача: Найдите стороны параллелограмма, если две его стороны относятся как 4:5, а периметр
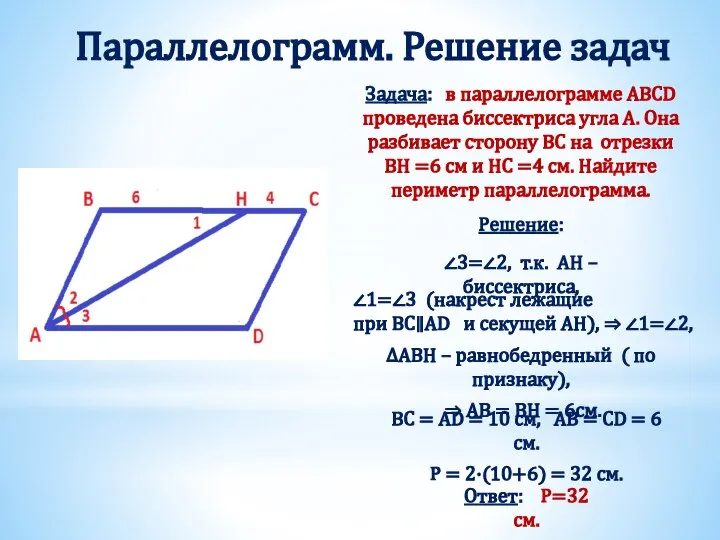
- 8. Параллелограмм. Решение задач Задача: в параллелограмме ABCD проведена биссектриса угла А. Она разбивает сторону ВС на
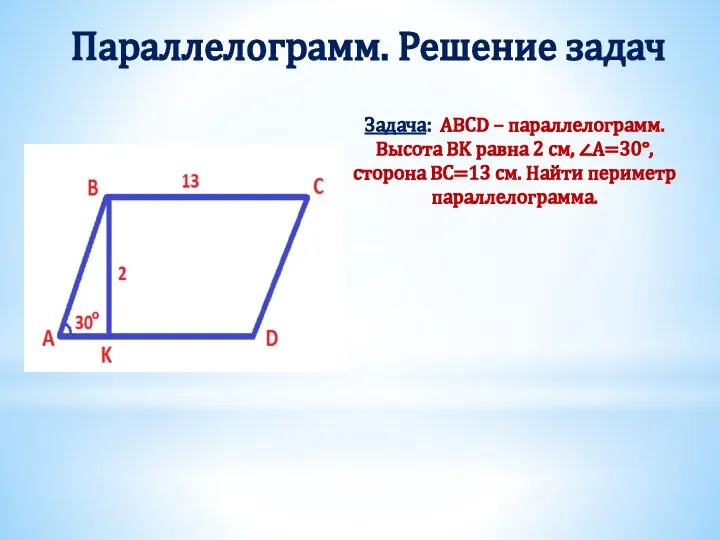
- 9. Параллелограмм. Решение задач Задача: ABCD – параллелограмм. Высота BK равна 2 см, ∠A=30°, сторона BC=13 см.
- 10. Решение задач по готовым чертежам с последующей самопроверкой
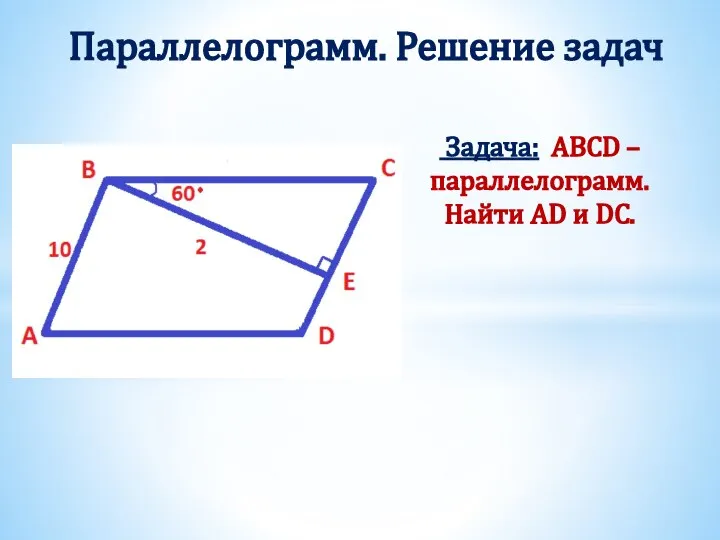
- 11. Задача: ABCD – параллелограмм. Найти AD и DC. Параллелограмм. Решение задач
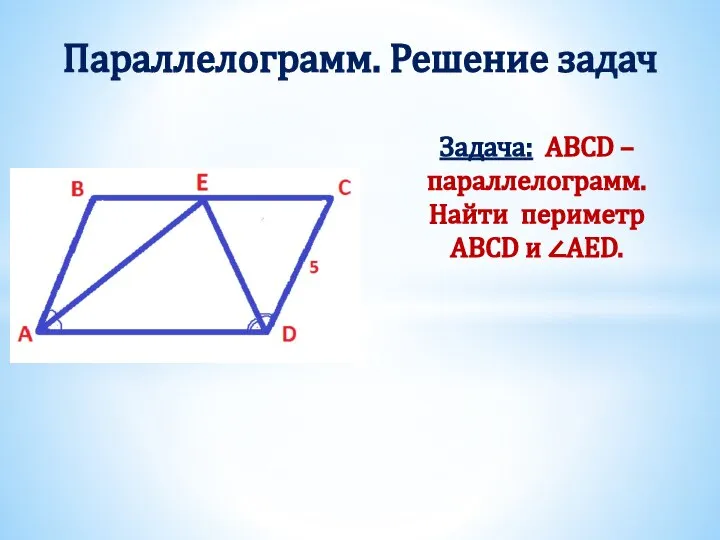
- 12. Задача: ABCD – параллелограмм. Найти периметр ABCD и ∠AED. Параллелограмм. Решение задач
- 13. Прямоугольник Прямоугольник – это параллелограмм, у которого все углы прямые. ∠A=∠B=∠C=∠D=90°
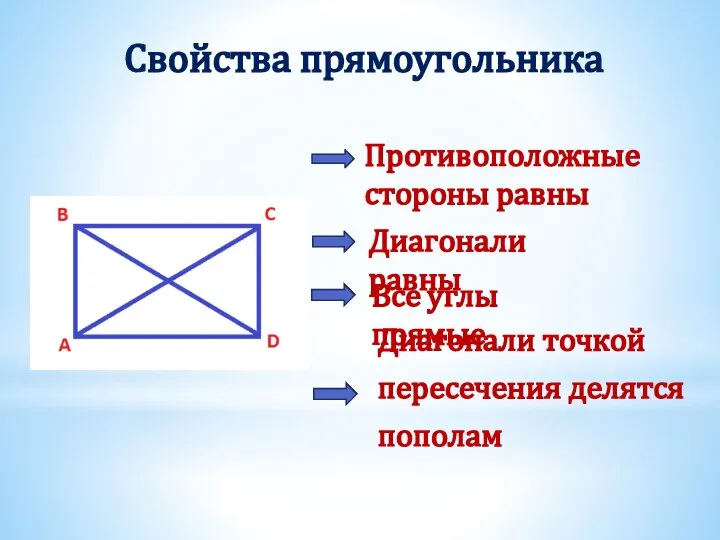
- 14. Свойства прямоугольника Противоположные стороны равны Все углы прямые Диагонали равны Диагонали точкой пересечения делятся пополам
- 15. Свойство диагоналей прямоугольника Диагонали прямоугольника равны. Доказательство: Прямоугольные треугольники BAD и CDA равны по двум катетам
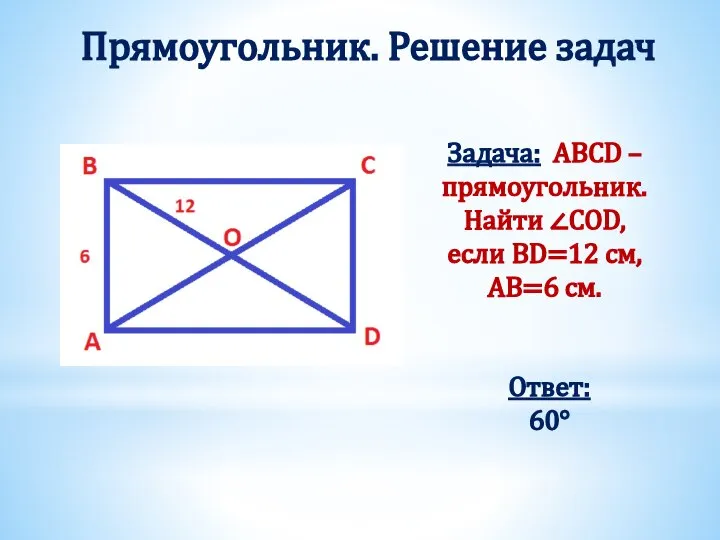
- 16. Прямоугольник. Решение задач Задача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см, AB=6 см. Ответ: 60°
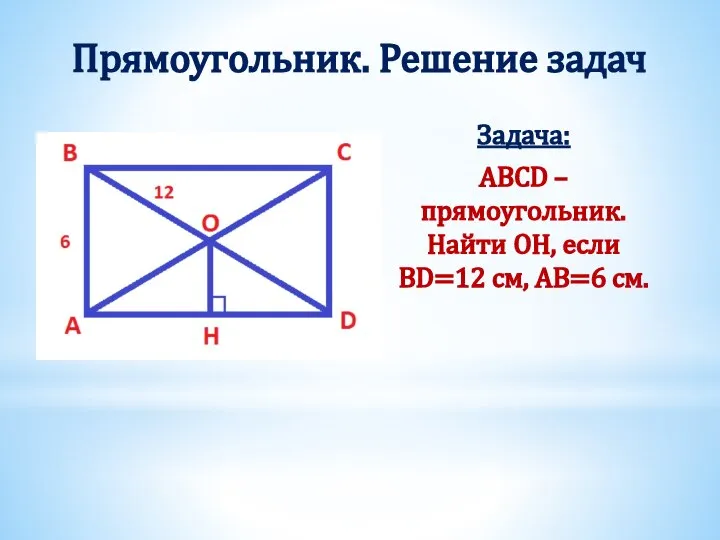
- 17. Прямоугольник. Решение задач Задача: ABCD – прямоугольник. Найти OН, если BD=12 см, AB=6 см.
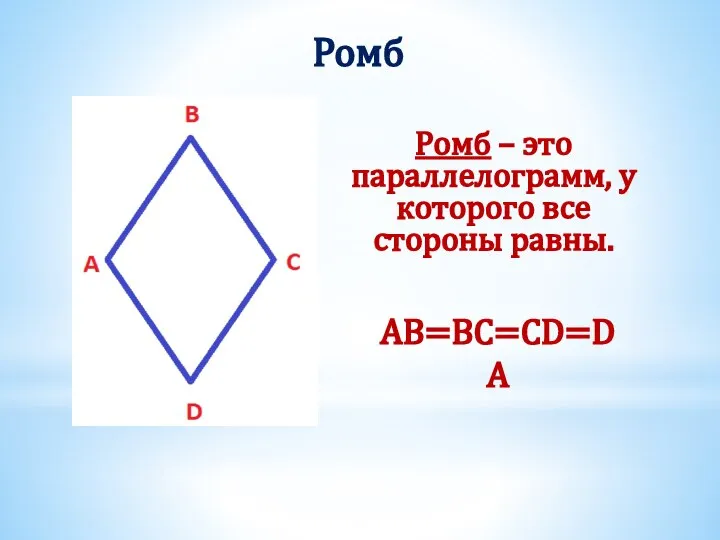
- 18. Ромб Ромб – это параллелограмм, у которого все стороны равны. AB=BC=CD=DA
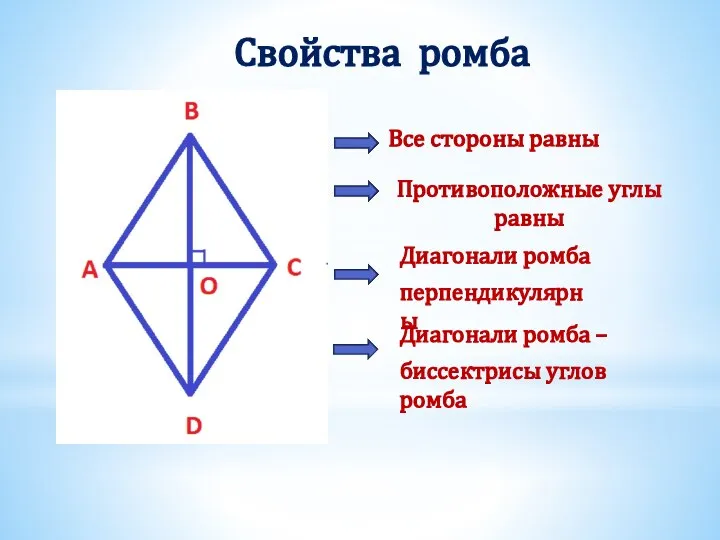
- 19. Свойства ромба Все стороны равны Противоположные углы равны Диагонали ромба перпендикулярны Диагонали ромба – биссектрисы углов
- 20. Свойства диагоналей ромба Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Доказательство: Рассмотрим ромб ABCD.
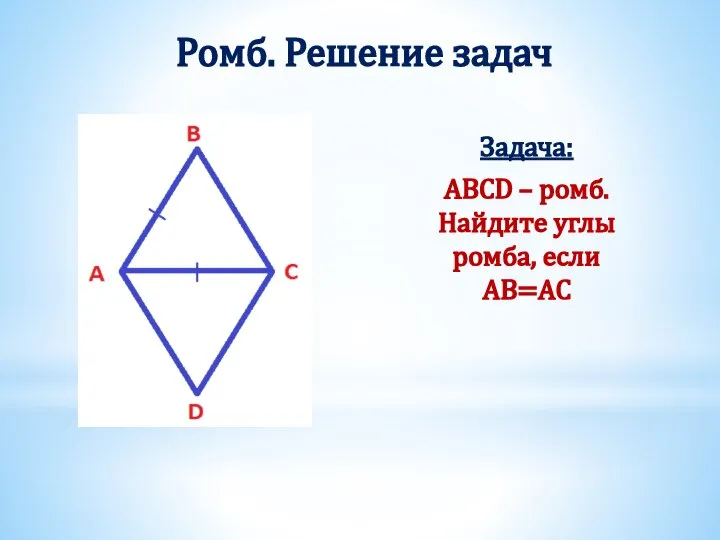
- 21. Ромб. Решение задач Задача: ABCD – ромб. Найдите углы ромба, если AB=AC
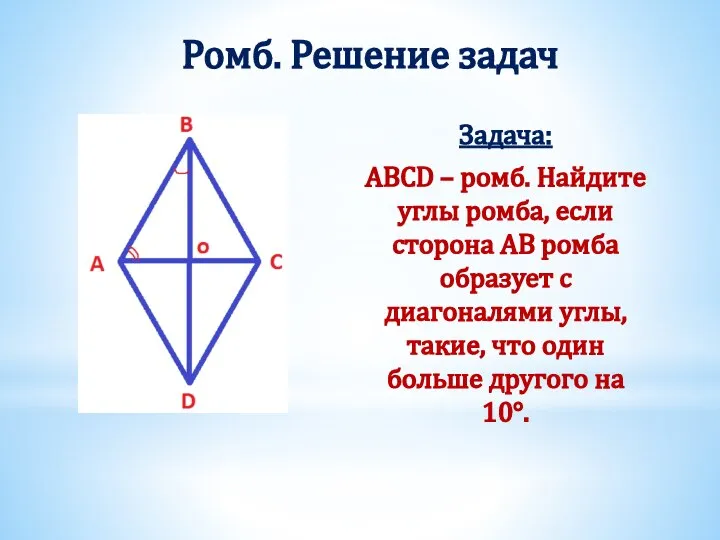
- 22. Ромб. Решение задач Задача: ABCD – ромб. Найдите углы ромба, если сторона АВ ромба образует с
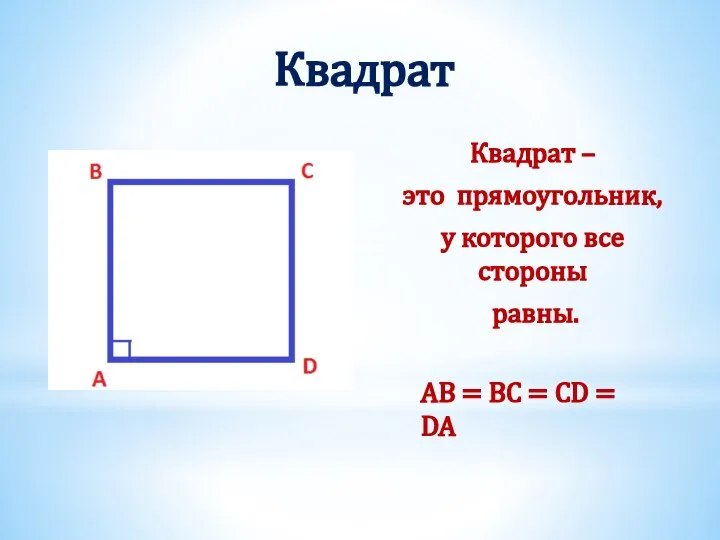
- 23. Квадрат Квадрат – это прямоугольник, у которого все стороны равны. AB = BC = CD =
- 25. Скачать презентацию




 Презентация на тему Тетраэдр
Презентация на тему Тетраэдр  Решение задач. Урок №68
Решение задач. Урок №68 Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах
ерпендикулярность прямых и плоскостей. Теорема о трех перпендикулярах Занимательные задачи (4 класс)
Занимательные задачи (4 класс) Численные методы механики сплошных сред. Метод граничных интегральных уравнений для задач гидромеханики
Численные методы механики сплошных сред. Метод граничных интегральных уравнений для задач гидромеханики Математика. Лекция 7. Приложения производной
Математика. Лекция 7. Приложения производной Квадратные уравнения
Квадратные уравнения Основы комбинаторики
Основы комбинаторики Замечательные точки треугольника
Замечательные точки треугольника Деление
Деление Степень.Симон Стевин
Степень.Симон Стевин Множество значений тригонометрических функций
Множество значений тригонометрических функций Параллельность прямых в пространстве
Параллельность прямых в пространстве Устный счёт
Устный счёт Урок математики в 4 классе по теме: « Приёмы письменного умножения трёхзначных чисел на однозначные». Урок 5
Урок математики в 4 классе по теме: « Приёмы письменного умножения трёхзначных чисел на однозначные». Урок 5 Пример записи решения задания к Части I РГР №1
Пример записи решения задания к Части I РГР №1 Стороны прямоугольника. Задачи
Стороны прямоугольника. Задачи Путешествие по математическому морю (1)
Путешествие по математическому морю (1) Деление на десятичную дробь
Деление на десятичную дробь Опыт по получению тени от различных фигур
Опыт по получению тени от различных фигур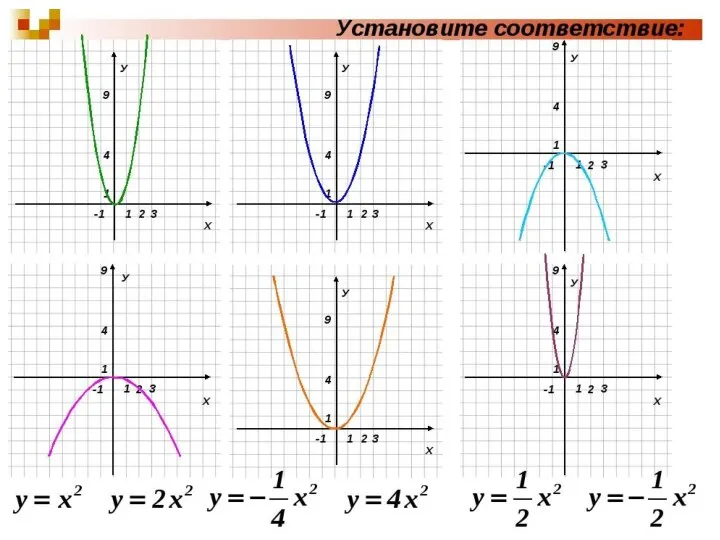 Графики функций
Графики функций Правильные многогранники
Правильные многогранники Единицы измерения объёма
Единицы измерения объёма نکات کلیدی روشهای محاسبه ضرایب و جداول
نکات کلیدی روشهای محاسبه ضرایب و جداول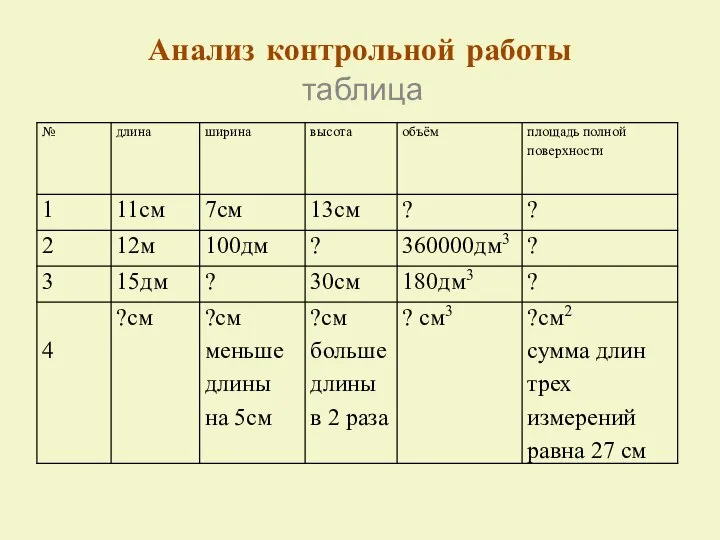 Таблицы и диаграммы. Чтение и составление таблиц
Таблицы и диаграммы. Чтение и составление таблиц Решение задания С-2 ЕГЭ
Решение задания С-2 ЕГЭ Методика эконометрических исследований
Методика эконометрических исследований