Содержание
- 2. Понятие множества и операции над ними Понятие множества является одним из основных понятий математики и поэтому
- 3. Стандартные обозначения числовых множеств N – множество всех натуральных чисел Z – множество всех целых чисел
- 4. Способы задания множеств 1. Способом перечисления всех его элементов. Например, если множество А состоит из чисел
- 5. 2. Через характеристическое свойство его элементов Характеристическое свойство – это такое свойство, которым обладает каждый элемент,
- 6. Символическая форма задания множеств А – это множество всех натуральных чисел, больших 3 и меньших 10
- 7. Отношения между множествами I. Рассмотрим 2 множества: А={a, b, c, d, e} B={b, d, k, m}
- 8. II. Рассмотрим 2 множества: А={a, b, c, d, e} B={k, m, n, f} Множества не имеют
- 9. III. Рассмотрим 2 множества: А={a, b, c, d, e} В={b, c, d} Эти множества называются пересекающимися,
- 10. IV. Рассмотрим 2 множества: А={a, b, c, d, e} В={c, d, a, b, e} Эти множества
- 11. Операции над множествами I. Пересечение множеств Пересечением множеств А и В называется множество, содержащее те и
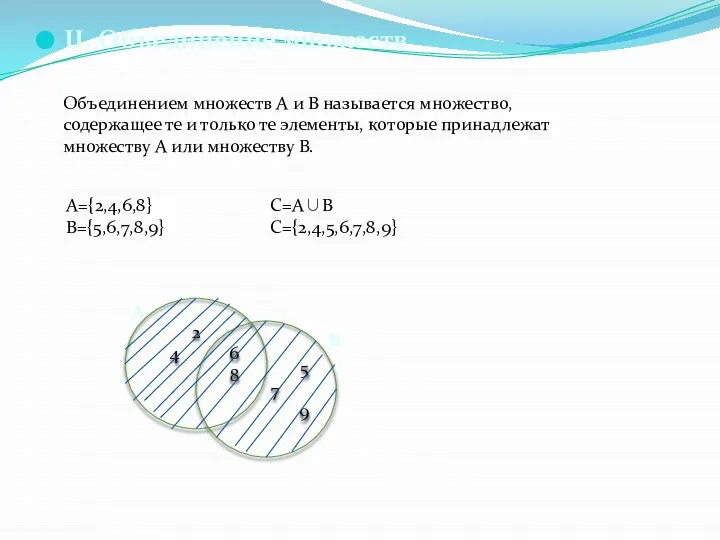
- 12. II. Объединение множеств Объединением множеств А и В называется множество, содержащее те и только те элементы,
- 13. III. Вычитание множеств Разностью множеств А и В называется множество, содержащее те и только те элементы,
- 14. Декартово произведение множеств Упорядоченную пару, образованную из элементов множеств А и В принято записывать, используя круглые
- 15. Пример 1 А={1,3,5} В={2,4} А·В={(1;2), (1;4), (3;2), (3;4), (5;2), (5;4)}
- 16. Пример 2 А={1,3,5} В=[2,4] или В={у|у Є R, 2≤у≤4}
- 17. Пример 3 А=[1;5] В={2,4}
- 18. Пример 4 А=[1;5] В=[2,4]
- 20. Скачать презентацию













![Пример 2 А={1,3,5} В=[2,4] или В={у|у Є R, 2≤у≤4}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182896/slide-15.jpg)
![Пример 3 А=[1;5] В={2,4}](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182896/slide-16.jpg)
![Пример 4 А=[1;5] В=[2,4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1182896/slide-17.jpg)
 Презентация на тему Устный счёт 1 класс
Презентация на тему Устный счёт 1 класс  Фундаментальные и прикладные исследования в метрологии
Фундаментальные и прикладные исследования в метрологии Проценты. Определение, обозначение, вычисление, применение Математика 5 класс
Проценты. Определение, обозначение, вычисление, применение Математика 5 класс Логарифмическая спираль
Логарифмическая спираль Презентация на тему Угол. Прямой и развернутый угол
Презентация на тему Угол. Прямой и развернутый угол  Вычитание числа 7
Вычитание числа 7 Свойства числовых неравенств. 8 класс
Свойства числовых неравенств. 8 класс Презентация на тему Приведение дробей к общему знаменателю (6 класс)
Презентация на тему Приведение дробей к общему знаменателю (6 класс)  Обыкновенные дроби
Обыкновенные дроби Обыкновенные дроби
Обыкновенные дроби parallelnost_1
parallelnost_1 Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве 2._3
2._3 Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования
Статистика. Статистика знает всё (Ильф и Петров). Выборочные исследования Теория о трех перпендикулярах
Теория о трех перпендикулярах Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1)
Matematika_5_klass_21_09_Chtenie_i_zapis_naturalnykh_chisel (1) Элементы линейной алгебры и геометрии выпуклых множеств
Элементы линейной алгебры и геометрии выпуклых множеств Задачи на части
Задачи на части Вероятность события
Вероятность события Цифра в 21 веке
Цифра в 21 веке Решение неравенств
Решение неравенств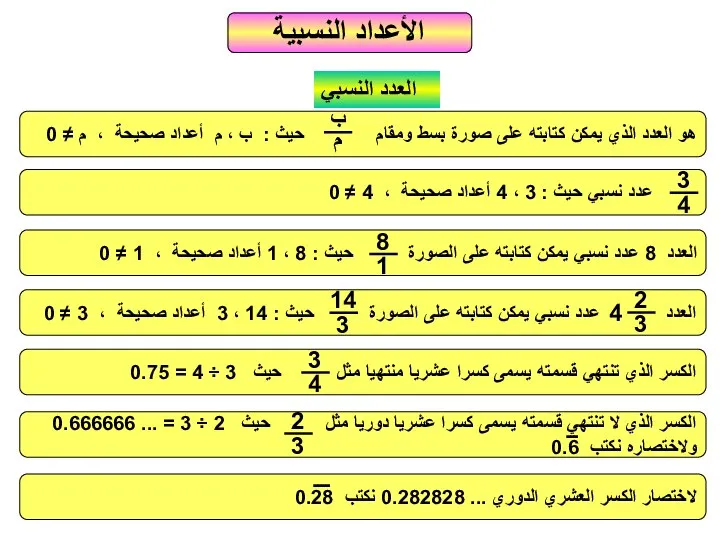 األعداد النسبية العدد النسبي ب
األعداد النسبية العدد النسبي ب Движение по окружности
Движение по окружности Математические структуры
Математические структуры Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи
Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи Игра
Игра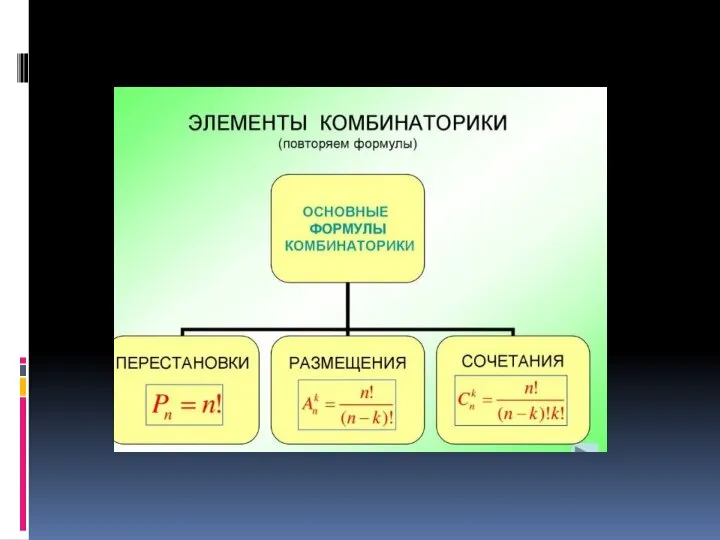 Основные понятия комбинаторики
Основные понятия комбинаторики Косинус угла
Косинус угла