Конус. Площадь поверхности конуса

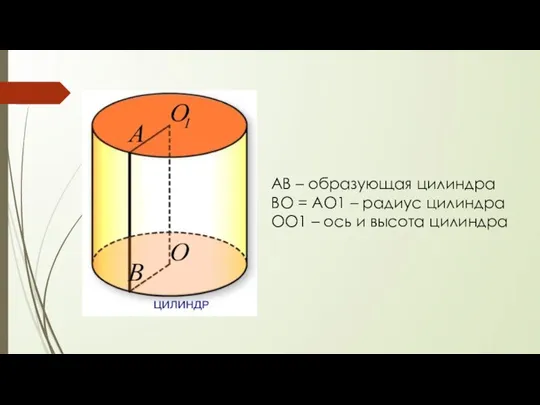
АВ – образующая цилиндра
ВО = АО1 – радиус цилиндра
ОО1 – ось и высота цилиндра

Вопрос №1:
Какая фигура является основанием цилиндра?
а) Овал
б) Круг
в) Квадрат

Вопрос №2:
Чему равна площадь основания цилиндра с радиусом 2см?
а) 4π
б) 8π
в) 4
2 см

Вопрос №3:
Как называется отрезок АВ?
а) диагональ цилиндра
б) апофема цилиндра
в)образующая цилиндра

Вопрос №4:
По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRh
б) 2πR(h+R);
в) πR2h

Вопрос №5:
По какой формуле можно вычислить полную поверхность цилиндра?
а) πR2h
б) 2πRh
в) 2πR(h+R)

Вопрос №6:
Вычислите боковую поверхность
данного цилиндра.
а) 15π см2
б) 30π см2
в) 48π см2
5 см
3 см

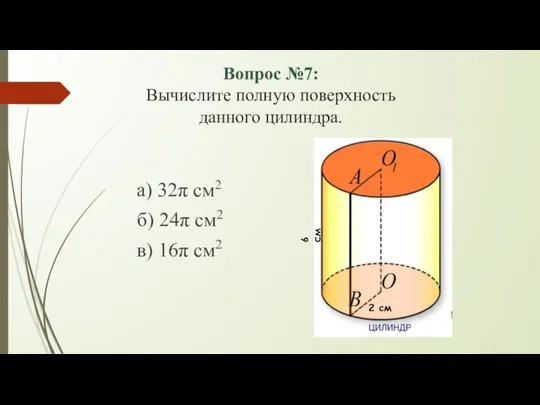
Вопрос №7:
Вычислите полную поверхность
данного цилиндра.
а) 32π см2
б) 24π см2
в) 16π см2
6 см
2 см

Вопрос №8:
Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей 3см?
а) 6 см2
б) 3 см2
в) 6π см2

Правильные ответы:
На оценку «5»-8 правильных ответов.
На оценку «4»- 6-7 правильных ответов.
На оценку «3»- 5 правильных ответов.
На оценку «2»- 4 и менее правильных ответов.

Конус в переводе с греческого «konos» означает «кегля», «верхушка шлема»
«сосновая шишка», остроконечный предмет.
Этот термин встречается у Евклида и Архимеда.
Историческая справка о конусе

Архимед
(287 до н. э. — 212 до н. э.)
В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров.

Демокрит
(470-380 гг. до н.э.)
Демокрит получил формулу для вычисления объема пирамиды и конуса.

Платон
(428-348 гг. до н.э.).
Школе Платона принадлежит:
а) исследование свойств призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.

Аполлоний Пергский
(260-170 гг. до н.э.)
Написал большой трактат
о конических сечениях

Конус выноса (геология)
Конус выноса — Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.

КОНУС НАРАСТАНИЯ (биология)
Конус нарастания: 1 — внешний вид верхушки побега водяной сосенки; 2, 3 — конус нарастания её стебля с поверхности и в разрезе.
Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.

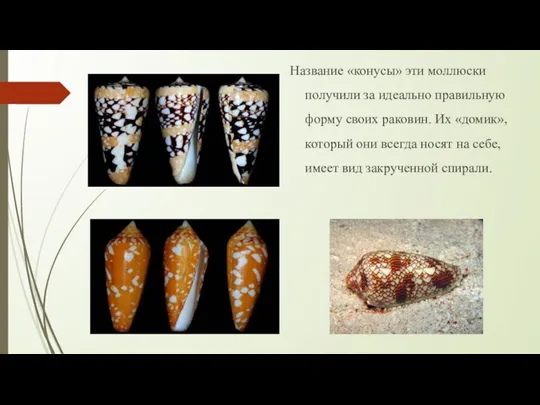
Конусы – ядовитые моллюски?
Конусы – это представители брюхоногих моллюсков, они получили известность среди ученых не только за свои невообразимые окрасы и формы, но и за свою ядовитость.

Название «конусы» эти моллюски получили за идеально правильную форму своих раковин. Их «домик», который они всегда носят на себе, имеет вид закрученной спирали.

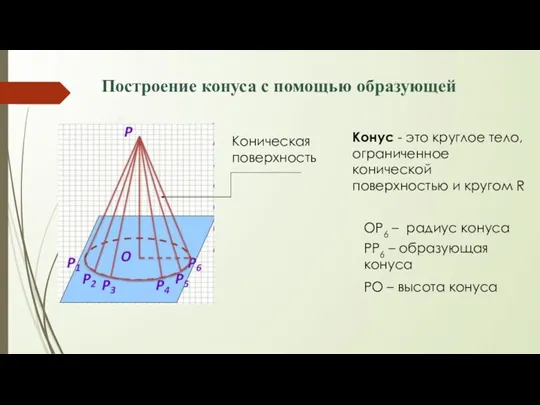
Построение конуса с помощью образующей
Коническая поверхность
Конус - это круглое тело, ограниченное конической поверхностью и кругом R
ОP6 – радиус конуса
PP6 – образующая конуса
PO – высота конуса

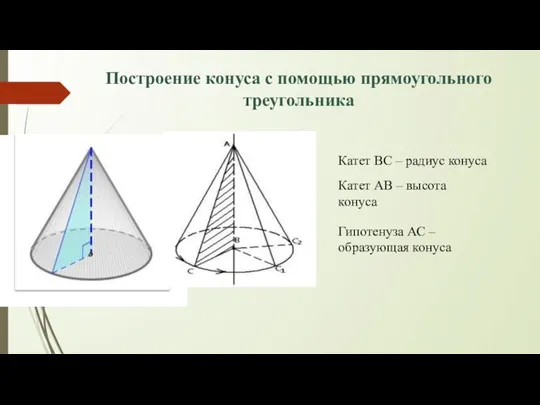
Построение конуса с помощью прямоугольного треугольника
Катет ВС – радиус конуса
Катет АВ – высота конуса
Гипотенуза АС – образующая конуса

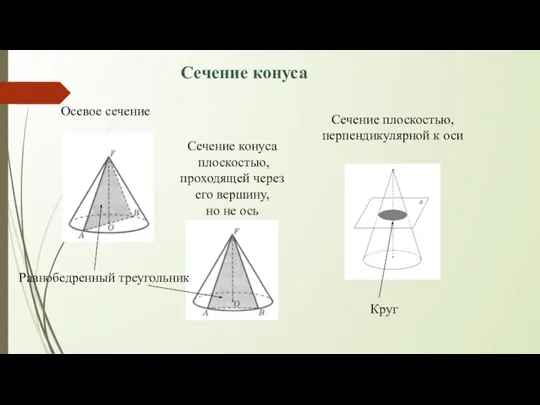
Сечение конуса
Осевое сечение
Сечение плоскостью, перпендикулярной к оси
Сечение конуса
плоскостью,
проходящей через его вершину,
но не ось
Круг
Равнобедренный треугольник

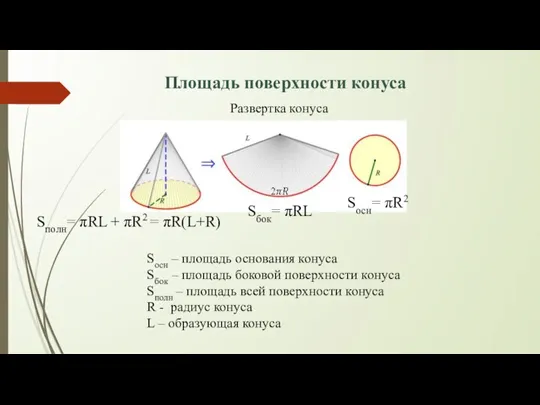
Развертка конуса
Sбок= πRL
Sосн= πR2
Sполн= πRL + πR2 = πR(L+R)
Площадь поверхности конуса
Sосн – площадь основания конуса
Sбок – площадь боковой поверхности конуса
Sполн – площадь всей поверхности конуса
R - радиус конуса
L – образующая конуса

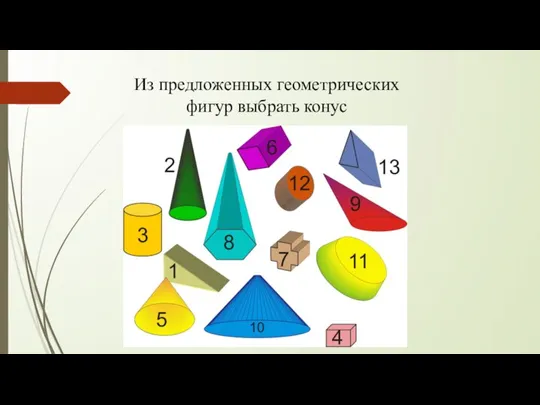
Из предложенных геометрических фигур выбрать конус

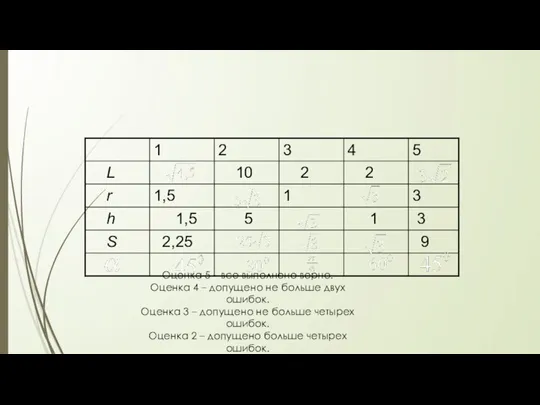
Оценка 5 – все выполнено верно.
Оценка 4 – допущено не больше двух ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.