Слайд 2Корень n-ой степени.
Ребята, мы продолжаем изучать корни n-ой степени из действительного числа.

Как и практически все математические объекты корни n-ой степени обладают некоторыми свойствами, сегодня мы и займемся изучением этих свойств.
Все свойства, которые мы с вами рассмотрим, формулируются и доказываются только для неотрицательных значений переменных, содержащихся под знаком корня.
Однако заметим, в случае нечетного показателя корня они выполняются и для отрицательных переменных.
Слайд 3Корень n-ой степени.
Теорема1.
Корень n-ой степени из произведения двух неотрицательных чисел равен

произведению корней n-ой степени этих чисел:
Слайд 4Корень n-ой степени.
Теорема2.
Если а≥0, b>0 и n – натуральное число, большее

одного тогда выполняется следующее равенство:
То есть корень n-ой степени частного равен частному корней n-ой степени.
Слайд 5Корень n-ой степени.
Пример. Вычислить
Решение. Воспользуемся теоремой 1
Пример. Вычислить
Решение. Представим подкоренное выражение в

виде неправильной дроби:
Воспользуемся теоремой 2:
Слайд 6Корень n-ой степени.
Пример. Вычислить
а)
б)
Решение.
а)
б)

Слайд 7Корень n-ой степени.
Теорема3.
Если a≥0, k – натуральное число и n – натуральное

число, больше 1, то справедливо равенство:
Чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение.
Слайд 8Корень n-ой степени.
Теорема4.
Если a≥0, n,k – натуральные числа, большие одного, то

справедливо равенство:
Чтобы извлечь корень из корня, достаточно перемножить показатели корней.
Пример.
Слайд 9Корень n-ой степени.
Теорема 5.
Если показатели корня и подкоренного выражения умножить на

одно и тоже натуральное число, то значение корня не изменится:
Слайд 10Корень n-ой степени.
Примеры:
Пример. Выполнить действия:
Решение.
Показатели корней разные числа, поэтому мы не

можем воспользоваться теоремой1, но воспользовавшись теоремой5 мы можем получить равные показатели.









 параллельность
параллельность Развитие умения рассуждать младшими школьниками при изучении элементов математической логики
Развитие умения рассуждать младшими школьниками при изучении элементов математической логики Задача линейного программирования. Канонический вид задачи линейного программирования
Задача линейного программирования. Канонический вид задачи линейного программирования Презентация на тему "Взаимно обратные числа" 6 класс
Презентация на тему "Взаимно обратные числа" 6 класс  Математическая разминка
Математическая разминка Соотношение между сторонами и углами треугольника
Соотношение между сторонами и углами треугольника Цилиндр
Цилиндр Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс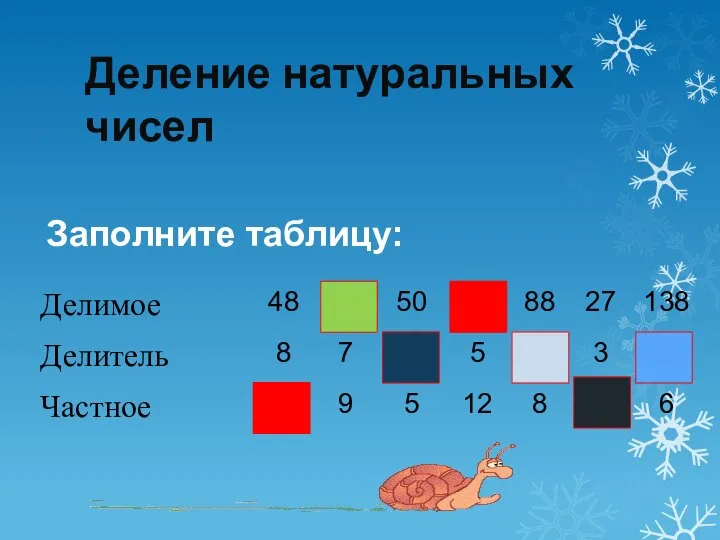 Деление натуральных чисел
Деление натуральных чисел Теория вероятности в жизни пчел
Теория вероятности в жизни пчел Вершины политопа числа разбиений
Вершины политопа числа разбиений Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)
Теория оптимальной фильтрации и управления. Лекция № 7 (3/2)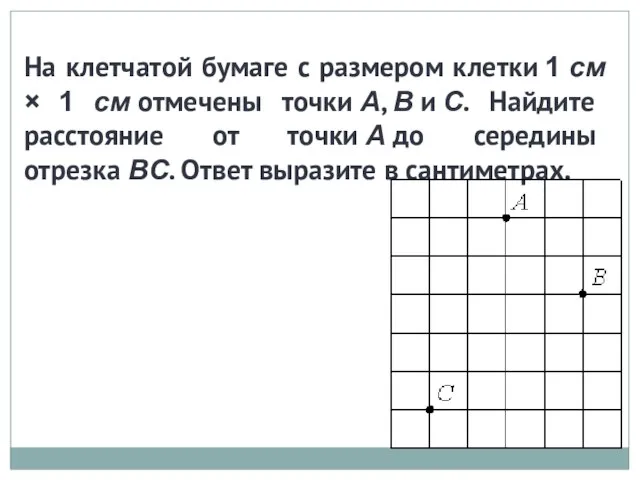 Решение задач
Решение задач Доли. Математический диктант
Доли. Математический диктант Число и цифра 5. Дидактическое пособие для детей 4-5 лет
Число и цифра 5. Дидактическое пособие для детей 4-5 лет Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Возведение в степень
Возведение в степень Презентация на тему Вычитание однозначного числа из двузначного с переходом через разряд (викторина) 2 класс
Презентация на тему Вычитание однозначного числа из двузначного с переходом через разряд (викторина) 2 класс  Золотое сечение - красота и гармония в математических расчетах
Золотое сечение - красота и гармония в математических расчетах Решение квадратных уравнений
Решение квадратных уравнений Деление на 2
Деление на 2 Простейшие тригонометрические уравнения, содержащие тангенс или котангенс
Простейшие тригонометрические уравнения, содержащие тангенс или котангенс Изображение пространственных фигур на плоскости
Изображение пространственных фигур на плоскости Презентация на тему Медиана, биссектриса и высота треугольника
Презентация на тему Медиана, биссектриса и высота треугольника  Сложение и вычитание обыкновенных дробей. Графический диктант
Сложение и вычитание обыкновенных дробей. Графический диктант Число и цифра 5
Число и цифра 5 Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12
Выпуклость и вогнутость, точки перегиба графика функции. Лекция 12