Содержание
- 2. Определения Пусть G = (V, E) – ориентированный граф. Поставим в соответствие каждому ребру e∈E в
- 3. Нахождение кратчайшего пути из одного источника
- 4. Алгоритм Дейкстры Идея алгоритма Дейкстры нахождения кратчайших путей из одной вершины во все другие состоит в
- 5. Алгоритм Дейкстры Вход: G= (V, E) – ориентированный граф, v0 ∈V – источник, c : E
- 6. Алгоритм Дейкстры Метод: Строим такое множество S ⊆ V, что кратчайший путь из источника в каждый
- 7. Алгоритм Дейкстры - O(n2) { S ← {v0}; D[v0] ← 0; для всех v ∈V \
- 8. Алгоритм Дейкстры. Пример № S w D[w] D[1] D[2] D[3] D[4] 0 {0} - - 2
- 9. Алгоритм Беллмана-Форда Задача: Для заданного взвешенного графа G=(V, E) найти кратчайшие пути из заданной вершины s
- 10. Алгоритм Беллмана-Форда
- 11. Алгоритм Беллмана-Форда bool FordBellman(s): for v ∈ V d[v] ← ∞ d[s] ← 0 for i
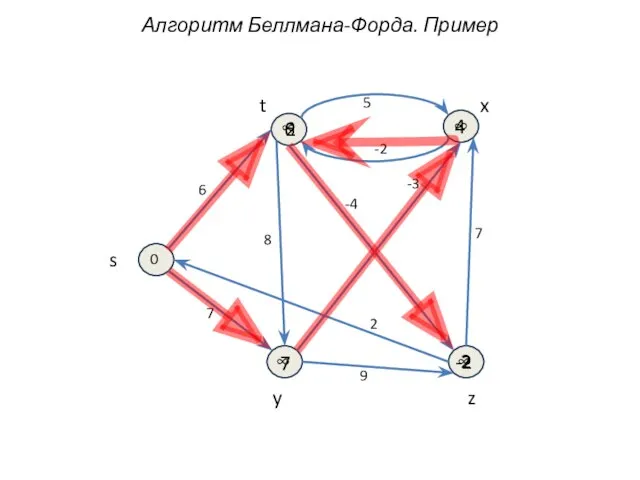
- 12. Алгоритм Беллмана-Форда. Пример t z y x s 7 -3 -4 2 9 8 7 -2
- 13. Алгоритм Беллмана-Форда Оценка сложности алгоритма: Инициализация занимает Θ(V) времени, каждый из |V|−1 проходов требует Θ(E) времени,
- 14. Нахождение кратчайших путей между всеми парами вершин
- 15. Алгоритм Флойда-Уоршолла Пусть G= (V, E) – ориентированный граф, c : E →R+ – функция стоимости
- 16. Алгоритм Флойда-Уоршолла Обозначим через dij(k) стоимость кратчайшего пути из вершины с номером i в вершину с
- 17. Алгоритм Флойда-Уоршолла Floyd-Warshall(M, n) { D(0) ← M; for k ← 1 to n do for
- 18. Транзитивное замыкание графа Пусть G= (V, E) ориентированный граф. Транзитивным замыканием графа G называется граф G′
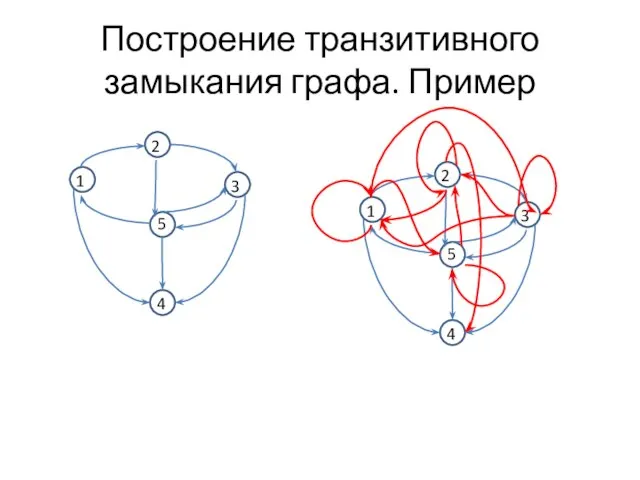
- 19. Построение транзитивного замыкания графа. Пример 1 3 2 5 4 1 3 2 5 4
- 20. Построение транзитивного замыкания графа Обозначим через tij(k) наличие пути из вершины с номером i в вершину
- 22. Скачать презентацию





![Алгоритм Дейкстры - O(n2) { S ← {v0}; D[v0] ← 0; для](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840210/slide-6.jpg)
![Алгоритм Дейкстры. Пример № S w D[w] D[1] D[2] D[3] D[4] 0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840210/slide-7.jpg)


![Алгоритм Беллмана-Форда bool FordBellman(s): for v ∈ V d[v] ← ∞ d[s]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840210/slide-10.jpg)







 Приложения производной
Приложения производной 3.7. Непрерывность функции
3.7. Непрерывность функции Порядок выполнения действий
Порядок выполнения действий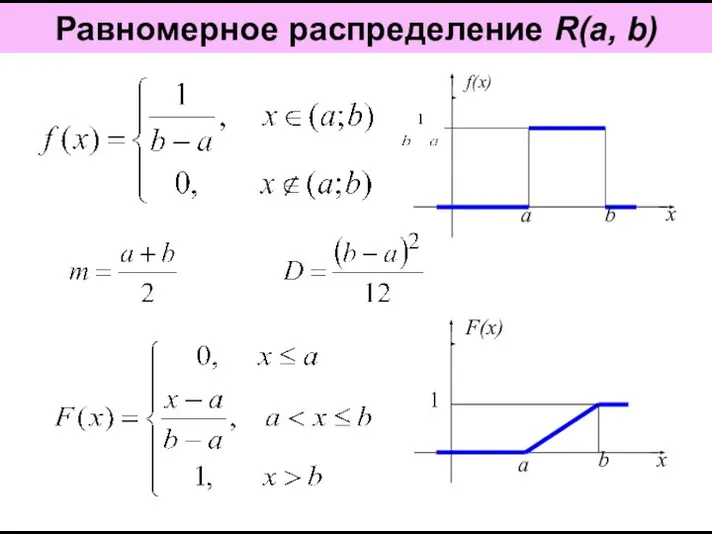 Равномерное распределение R(a, b)
Равномерное распределение R(a, b) Введение в геометрию
Введение в геометрию Равенство фигур
Равенство фигур Приближенные значения чисел. Округление
Приближенные значения чисел. Округление Прямое сложение и вычитание
Прямое сложение и вычитание Роль теории коммуникации, теории информации,теории вероятностей
Роль теории коммуникации, теории информации,теории вероятностей Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Решение примеров и задач с числами, полученными при измерении стоимости
Решение примеров и задач с числами, полученными при измерении стоимости Презентация на тему Геометрическая прогрессия
Презентация на тему Геометрическая прогрессия  Центральные углы
Центральные углы Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)  Степенная функция с целым показателем
Степенная функция с целым показателем Иррациональные уравнения
Иррациональные уравнения Число. Имя числительное
Число. Имя числительное Числа, кратные 3
Числа, кратные 3 Производные тригонометрических функций. 10 класс
Производные тригонометрических функций. 10 класс Числа - близнецы
Числа - близнецы Геймификация образовательного процесса на уроках математики с использованием двигательной активности
Геймификация образовательного процесса на уроках математики с использованием двигательной активности Презентация на тему Квадратичная функция. Графики функций
Презентация на тему Квадратичная функция. Графики функций  Преобразование выражений, содержащих модуль
Преобразование выражений, содержащих модуль Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Элементы теории вероятностей и математической статистики и их применение в расчетах надежности
Элементы теории вероятностей и математической статистики и их применение в расчетах надежности Применение производной в географии
Применение производной в географии Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Презентация по математике "Число 5. Цифра 5" -
Презентация по математике "Число 5. Цифра 5" -