Содержание
- 2. поговорим о прямоугольном параллелепипеде вспомним некоторые из его свойств выведем формулы для вычисления объема прямоугольного параллелепипеда
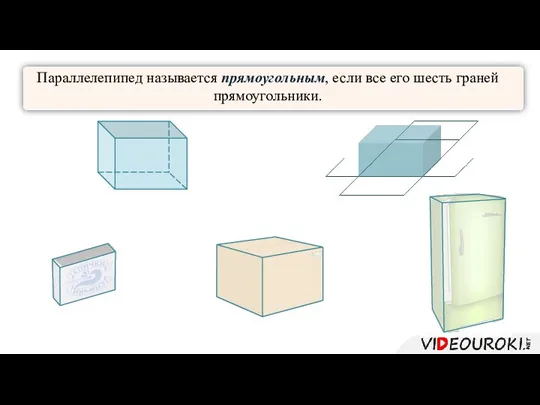
- 3. Параллелепипед называется прямоугольным, если все его шесть граней прямоугольники.
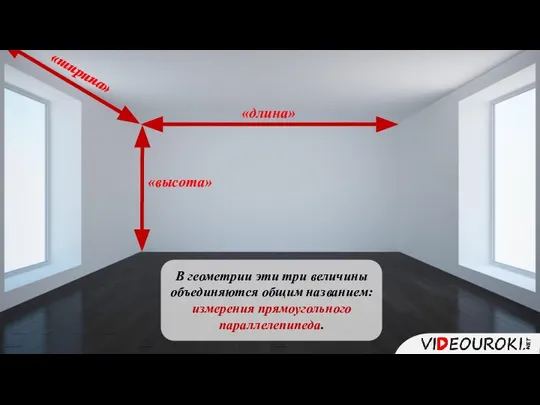
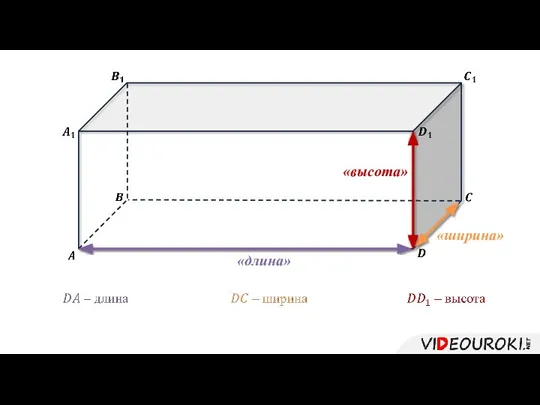
- 4. «длина» «ширина» «высота» В геометрии эти три величины объединяются общим названием: измерения прямоугольного параллелепипеда.
- 5. «ширина» «длина» «высота»
- 6. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Свойства прямоугольного параллелепипеда: Объем прямоугольного параллелепипеда
- 7. Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Доказательство. Что и требовалось доказать.
- 8. Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений. Доказательство.
- 9. Следствие. Объем прямоугольного параллелепипеда равен произведению площади основания на высоту. Доказательство. Что и требовалось доказать.
- 10. Следствие. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. Доказательство.
- 11. Замечание. Поэтому площадь построенного на ней квадрата вдвое больше площади данного квадрата. Таким образом, не составляет
- 12. Замечание. Эта задача получила название: «задача об удвоении куба». Одновременно им была доказана неразрешимость еще одной
- 13. Решение.
- 14. Решение.
- 16. Скачать презентацию










 Prezentatsia_2
Prezentatsia_2 Умножение дробей. Устная работа
Умножение дробей. Устная работа Время. Единицы времени
Время. Единицы времени Формулы. Повторение
Формулы. Повторение Представление множеств ЭВМ
Представление множеств ЭВМ Презентация на тему Математическая викторина
Презентация на тему Математическая викторина  Операции, функции, выражения
Операции, функции, выражения Математический ребус
Математический ребус Геометрия до Евклида
Геометрия до Евклида Основы векторного исчисления
Основы векторного исчисления Формирование элементарных математических представлений
Формирование элементарных математических представлений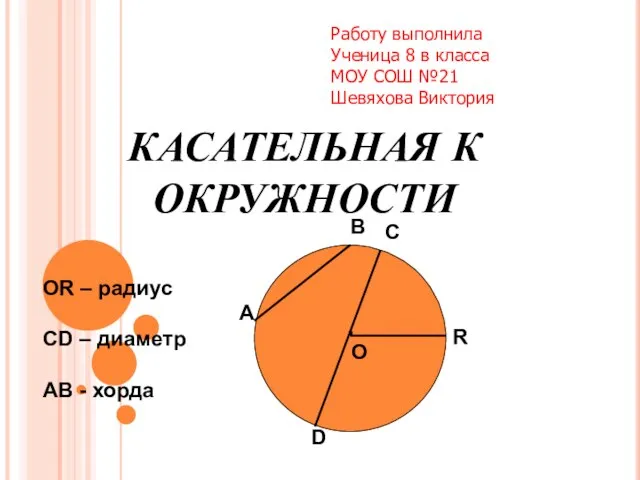 Презентация на тему Касательная к окружности
Презентация на тему Касательная к окружности  Технология квантового обучения в преподавании математики
Технология квантового обучения в преподавании математики Случайные сигналы и их математические модели
Случайные сигналы и их математические модели Опыт по получению тени от различных фигур
Опыт по получению тени от различных фигур Отрезок. Сравнение отрезков
Отрезок. Сравнение отрезков розвязування трикутників
розвязування трикутників Основы метрологического обеспечения
Основы метрологического обеспечения Решение логических задач с помощью таблиц и метода рассуждений
Решение логических задач с помощью таблиц и метода рассуждений Урок математики во 2 классе
Урок математики во 2 классе Движения
Движения Соотношения между сторонами и углами в треугольнике
Соотношения между сторонами и углами в треугольнике Упрощение выражений. Урок с использованием ИКТ
Упрощение выражений. Урок с использованием ИКТ Графики функций. Задания
Графики функций. Задания Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Случаи сложения вида +6
Случаи сложения вида +6 Задачи. вариант 3
Задачи. вариант 3 Презентация на тему Математическая модель
Презентация на тему Математическая модель