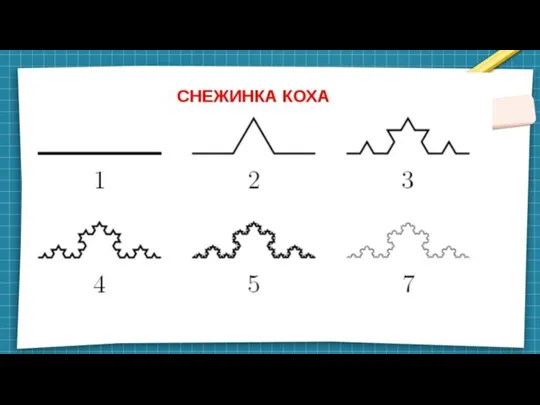
Слайд 2Кривая Коха
1904г. Хельге Фон Кох, статья «Об одной непрерывной кривой, не имеющей

касательной, построенной с помощью методов элементарной геометрии»
Кривая Коха нигде не дифференцируема и не спрямляема.
Кривая Коха имеет бесконечную длину.
Кривая Коха не имеет самопересечений.
Кривая Коха имеет промежуточную хаусдорфову размерность, которая равна 1,26
Длина кривой Коха описывается выражением
K_n=(4/3)^n→ бесконечность
Слайд 4Кривая Коха
void DrawKoch( double dir, double len, int n)
{ double dirRad=0.0174533*dir;
if

(n= =0) lineRel(len*cos(dirRad), len*sin(dirRad));
else
{ n--;
len/=3;
DrawKoch(dir,len,n);
dir+=60;
DrawKoch(dir,len,n);
dir-=120;
DrawKoch(dir, len,n);
dir+=60
DrawKoch(dir,len,n); }
}
Слайд 6Вариации кривой Коха
Квадратичная кривая Коха

Слайд 7Вариации кривой Коха
Поверхность Коха

Слайд 8Квадратичная поверхность Коха

Слайд 10Дробная размерность
Когда речь идет об обычных геометрических объектах: линия, поверхность, шар, то

их топологические размерности известны и являются целыми числами.
Простой способ измерить длину кривых, площадь поверхности или объем тела состоит в том, чтобы разделить их на небольшие элементы – отрезки длиной 1/n, квадраты со стороной 1/sqrt(n) или на небольшие кубы с ребрами 1/кубический корень (n)
Слайд 11Дробная размерность (Хаусдорф, 1919)
Будем говорить, что объект имеет размерность D, если при

делении его на N равных частей, каждая часть будет иметь сторону меньшую чем сторона исходного объекта в r раз
r=(1/N)^(1/D)
Найдем отсюда D
D=log N/log (1/r)
Здесь N – количество частей, r – отношение длины ребра маленького объекта к большому.
Слайд 12Дробная размерность
Для кривой Коха N=4, r=1/3
D=ln 4/ln 3= 1.26…
Кривая Гильберта (1891г)

D=ln4 /ln 2 =2
Слайд 14Кривая Гильберта
Используется для выявления ошибок при передаче данных
Числа от 0 до

7 кодируются 000, 001, 010, 011, 100, 101, 110, 111
Каждое из чисел можно расположить в вершине единичного куба. Например, 001 – (0,0,1)
Если упорядочить числа, следуя кривой Гильберта, получим код Грея
Код Грея применяется для кодирования информации в сетях цифрового телевидения
Слайд 15Кривая Гильберта
Используется для цифровой обработки изображений
Например, для распечатки изображения в градациях

серого при ограниченной палитре оттенков.
При проходе палитры по кривой Гильберта отсутствуют дефекты изображения.
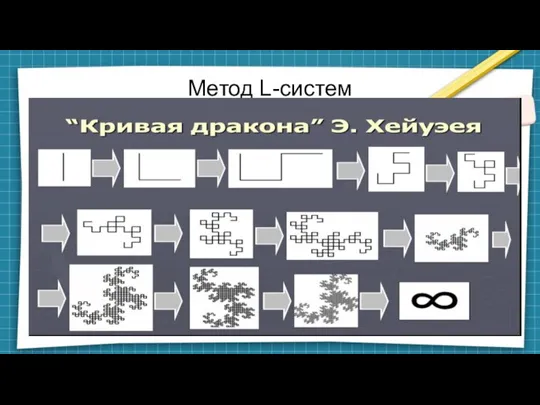
Слайд 16Метод L-систем
„ F“ – forward(1,1)
„+“ – turn(A)
„- „ – turn(-A)
Для A=60

S1= „F-F++F-F“
F→ „F-F++F-F“
S2=“(F-F++F-F)-(F-F++F-F)++(F-F++F-F)-(F-F++F-F)“
Слайд 17Метод L-систем
FILE *f1,*f2;
for(; ch!=EOF)
{
ch=fget(f1);
if(ch==“+“|| ch==“-“) fput(ch,f2);
else if(ch==“F“) fputs(f2,

„F-F++F-F“);
}
Слайд 18Метод L-систем
Подпрограмма для черепахи
for( each ch from f2)
{
If (ch==“+“) turn(A);

else if (ch==“-“) turn(-A);
else if (ch==“F“) forward(1,1);
}
Слайд 19Метод L-систем
„F“→ „F“
„X“→ „X+YF+“
„Y“→ „-FX-Y“
Если начальная строка atom=FX, то
s1=FX+YF+
s2=F(X+YF+)+(-FX-Y)F+
Что будет рисовать черепаха?

s1=F+F+, s2=F+F++-F-F+
Слайд 20Метод L-систем
s1=F+F+ (два отрезка под углом А)
s2=F+F++-F-F+ (два набора отрезков
)
Слайд 22Метод L-систем
void produceString( char *str, int order)
{ for(; *str; str++)
{ switch

(*str)
{ case’ +“: CD=A; break’
case „-“: CD=-A; break;
case „F“: if (order>0) produceString(Fstr, order-1);
else forward(len, 1); break;
case „X“ : if(order>0) produceString(Xstr, order-1);
case „Y“: if(order>0) produceString(Ystr, order-1);}
}
}
Слайд 23Метод L-систем
„[“ – затолкнуть в стек
„]“ – вытолкнуть из стека
// добавить в
![Метод L-систем „[“ – затолкнуть в стек „]“ – вытолкнуть из стека](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1014078/slide-22.jpg)
функцию produceString()
case „[“: saveTurtle(); break;
case „]“: restoreTurtle(); break;
Куст
F→“FF-[-F+F+F]+[+F-F-F]“
Слайд 24Задание
Записать инструкции для черепахи в виде L-строк для одной из квадратичных кривых

Коха
Вычислить размерность одной из квадратичных кривых Коха или дракона
Записать и нарисовать первые три поколения кривой
atom=YF, Fstr= F, Xstr= YF+XF+Y, Ystr=XF-YX-X, угол A=60
Нарисовать фрактал куст( три итерации, угол A=22.5)
F→FF-[-F+F+F]+[+F-F-F]
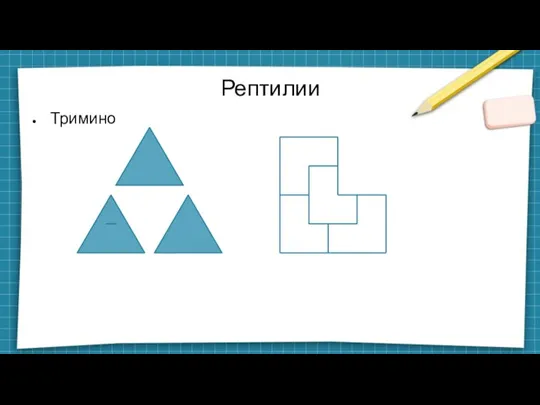
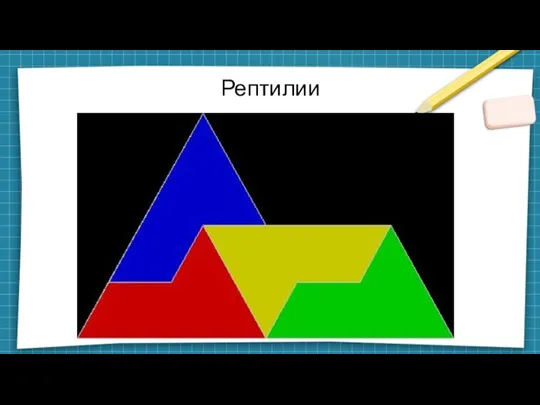
Слайд 26Рептилии
Класс непериодических мозаик
Рисуются от большого к малому или наоборот
Различные копии рептилии совмещаются

друг с другом, образуя большую рептилию
void trio( double size, int depth)
{ if (depth==1) draw();
else for( int i=0; i<4; i++)
{ draw1( size/2, depth-1);
}
}
Слайд 28Рептилии
Сфинкс (как разместить внутри 4 меньших сфинкса?)

Слайд 30Мозаика Пенроуза
Мозаика Пенроуза — общее название трёх особых типов непериодического разбиения плоскости;

названы по имени английского математика Роджера Пенроуза, исследовавшего их в 1970-е годы.
Все три типа, как и любые апериодические мозаики, обладают следующими свойствами:
непериодичность — отсутствие трансляционной симметрии,
повторяемость — любой сколь угодно большой фрагмент мозаики Пенроуза встречается в мозаике бесконечное число раз, хоть и через неравные расстояния,



















![Метод L-систем „[“ – затолкнуть в стек „]“ – вытолкнуть из стека](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1014078/slide-22.jpg)






 Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel
Нефть. Добыча, переработка, использование. Задачи на нахождение объёма цилиндра. Работа с формулами в таблице Excel Олимпиадная математика
Олимпиадная математика Цифровая азбука
Цифровая азбука Основные теоремы о дифференцируемых функциях
Основные теоремы о дифференцируемых функциях Краткая история появления и развития пределов
Краткая история появления и развития пределов С чего начать подготовку к ЕГЭ по профильной математике
С чего начать подготовку к ЕГЭ по профильной математике Признаки параллелограмма
Признаки параллелограмма Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Вертикальные углы
Вертикальные углы Задачки от жителей Солнечного города. 1 класс
Задачки от жителей Солнечного города. 1 класс Правила вычисления производной
Правила вычисления производной Математика в профессии строителя
Математика в профессии строителя Комплексные числа
Комплексные числа Площади фигур
Площади фигур Признаки параллельных прямых
Признаки параллельных прямых Решение задач на концентрацию при подготовке к ГИА
Решение задач на концентрацию при подготовке к ГИА Определение куба
Определение куба Системы уравнений
Системы уравнений Дифференциальные уравнения. Лекция
Дифференциальные уравнения. Лекция Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Мастер-класс в рамках игры физико-математические забавы
Мастер-класс в рамках игры физико-математические забавы График равномерного движения
График равномерного движения Обработка данных. Задачи локального и глобального интерполирования
Обработка данных. Задачи локального и глобального интерполирования Задачи, обратные данной
Задачи, обратные данной Презентация на тему Прямая и обратная пропорциональность Линейная функция
Презентация на тему Прямая и обратная пропорциональность Линейная функция  Комбинаторика. 11 класс
Комбинаторика. 11 класс Задачи на построение сечений
Задачи на построение сечений Характеристика структуры и содержания экзаменационной работы
Характеристика структуры и содержания экзаменационной работы