Содержание
- 2. “Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка
- 3. Родился Пифагор где-то между 600 и 590 гг. до Рождества Христова и жил около ста лет.
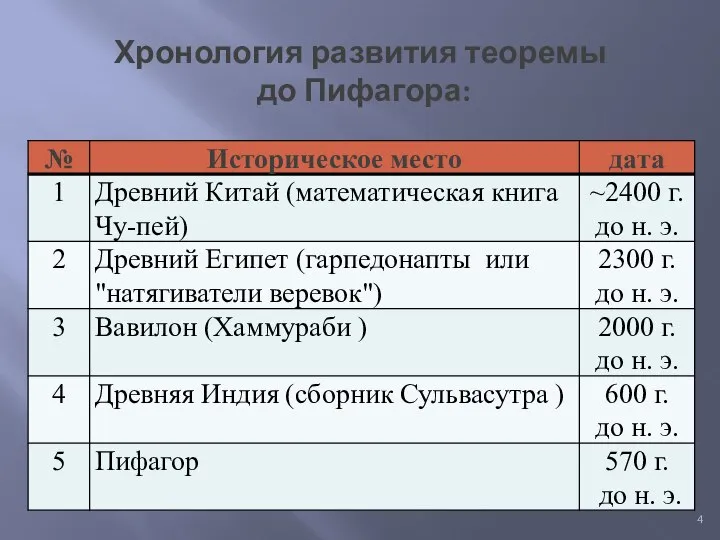
- 4. Хронология развития теоремы до Пифагора:
- 5. Исторический обзор начнём с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении
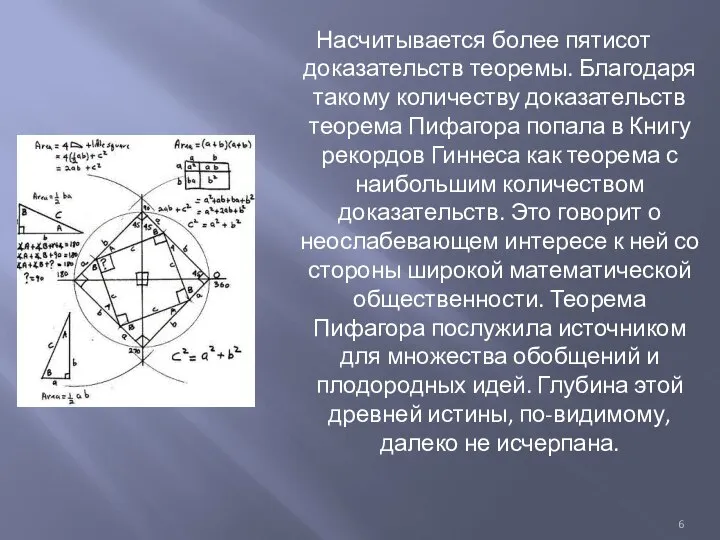
- 6. Насчитывается более пятисот доказательств теоремы. Благодаря такому количеству доказательств теорема Пифагора попала в Книгу рекордов Гиннеса
- 7. Приведём различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
- 8. Существует три формулировки теоремы Пифагора: 1. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. 2.
- 9. Теорема Пифагора – важнейшее утверждение геометрии. Даже те, кто в своей жизни навсегда «распрощался» с математикой,
- 10. Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. Доказательство Пифагора
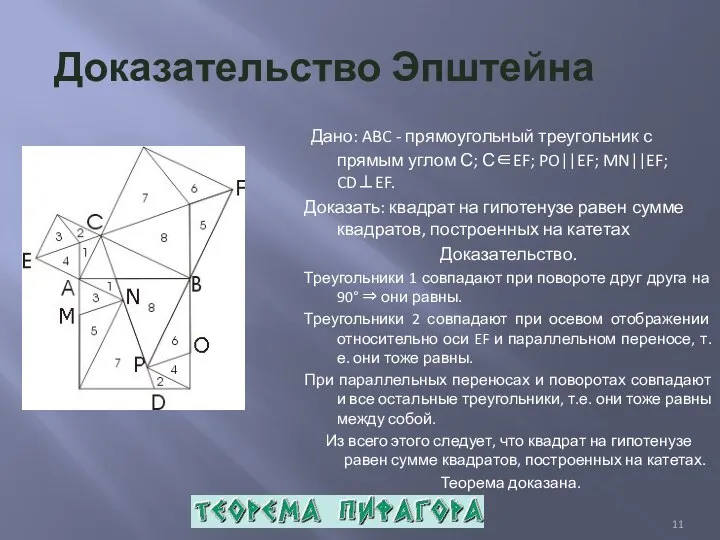
- 11. Доказательство Эпштейна Дано: ABC - прямоугольный треугольник с прямым углом С; С∈EF; PO||EF; MN||EF; CD⊥EF. Доказать:
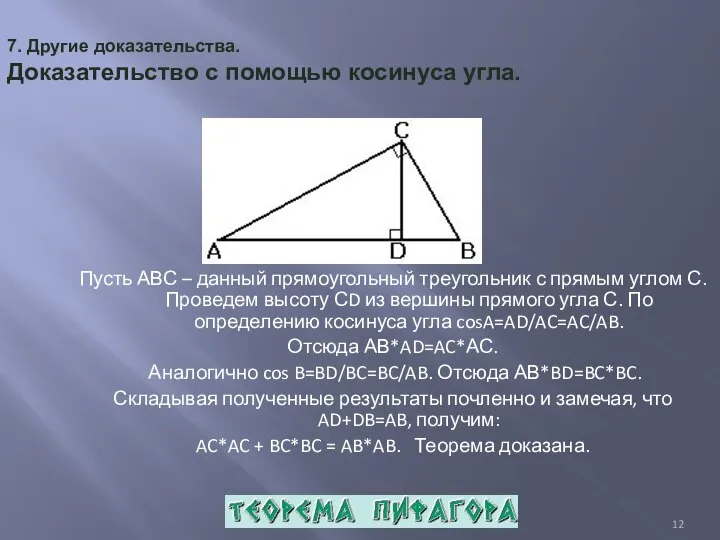
- 12. 7. Другие доказательства. Доказательство с помощью косинуса угла. Пусть АВС – данный прямоугольный треугольник с прямым
- 13. ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ ПО ТЕМЕ: "ТЕОРЕМА ПИФАГОРА".
- 14. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И
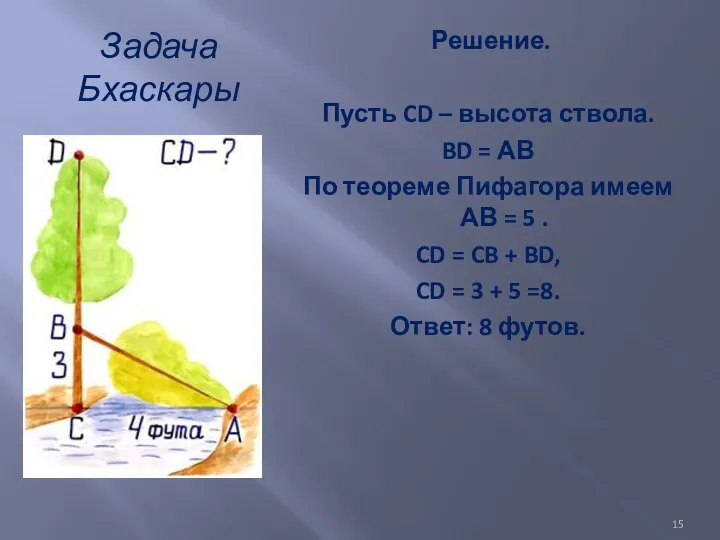
- 15. Задача Бхаскары Решение. Пусть CD – высота ствола. BD = АВ По теореме Пифагора имеем АВ
- 16. Практическое применение теоремы Пифагора
- 17. Считать приложения теоремы Пифагора только теоретическими - большая ошибка. Заметим, что расчёт площади кровли можно заметно
- 18. В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то
- 19. Пифагоровы тройки
- 20. Изучение свойств натуральных чисел привело пифагорейцев к ещё одной «вечной» проблеме теоретической арифметики (теории чисел) —
- 21. Сегодня эта задача именуется задачей Пифагора, а её решения — тройки натуральных чисел, удовлетворяющих уравнению (а2+b2=c2)—
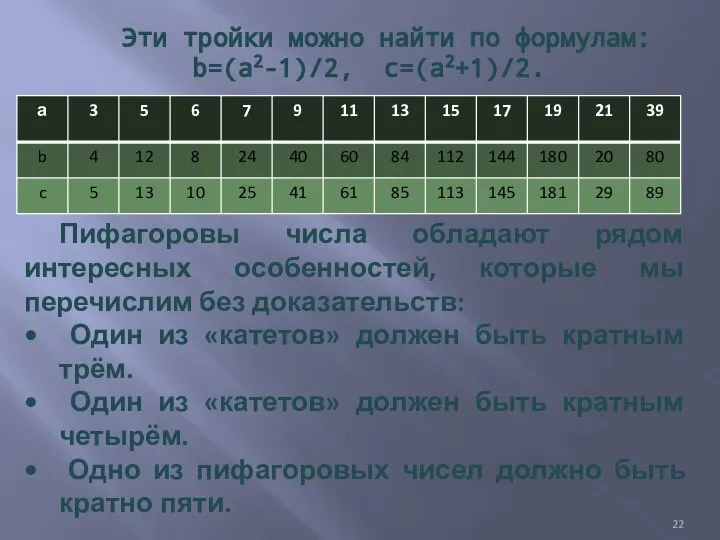
- 22. Эти тройки можно найти по формулам: b=(a2-1)/2, c=(a2+1)/2. Пифагоровы числа обладают рядом интересных особенностей, которые мы
- 23. Эпилог. Вечный кладезь мудрости.
- 24. И чем дальше неумолимое время уносит нас от времени Пифагора, тем острее видится поразительная прозорливость эллинского
- 25. Именно так определяет роль Пифагора в истории естествознания современный американский математик и историк науки М. Клайн:
- 27. Скачать презентацию

















 Векторы на плоскости
Векторы на плоскости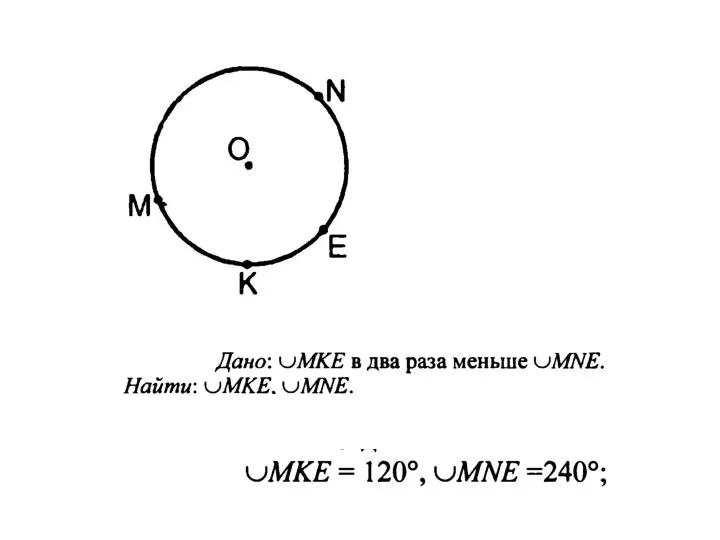 Теорема о вписанном угле
Теорема о вписанном угле Решение показательных неравенств
Решение показательных неравенств Сравнение, сложение и вычитание дробей с разными знаменателями
Сравнение, сложение и вычитание дробей с разными знаменателями Презентация на тему Простейшая геометрия
Презентация на тему Простейшая геометрия  Геометрические построения
Геометрические построения Метод Крамера
Метод Крамера Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Тетраэдр параллелепипед. 10 класс
Тетраэдр параллелепипед. 10 класс Л 5 Функция одной переменной
Л 5 Функция одной переменной Презентация на тему Степень с рациональным показателем (9 класс)
Презентация на тему Степень с рациональным показателем (9 класс)  Тупой угол равен прямому
Тупой угол равен прямому Логарифм и его свойства
Логарифм и его свойства Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Смежные и вертикальные углы
Смежные и вертикальные углы Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ  Геометричекие тела
Геометричекие тела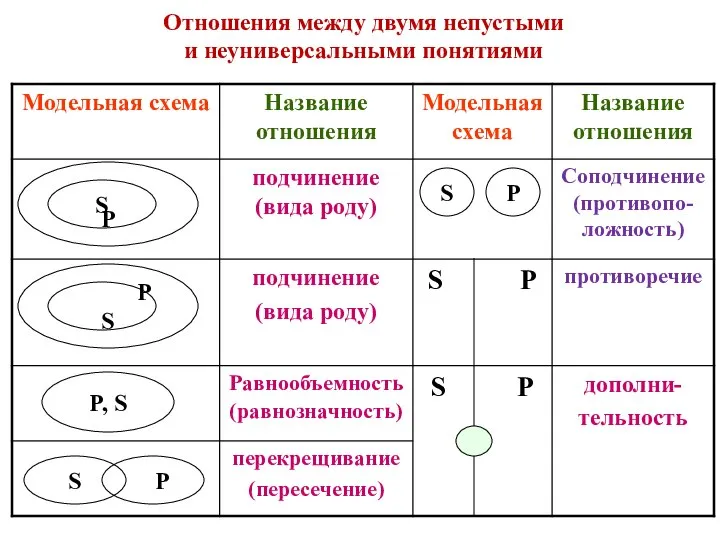 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Симметрия
Симметрия Десятичные дроби
Десятичные дроби Квадратные неравенства
Квадратные неравенства Статистические графики
Статистические графики Математика для марксистов
Математика для марксистов Считаем без ошибок. Задания для устного счёта
Считаем без ошибок. Задания для устного счёта Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Интеграл степенной функции с действительным показателем. Интеграл показательной функции
Интеграл степенной функции с действительным показателем. Интеграл показательной функции Сравнение отрезков и углов геометрических фигур
Сравнение отрезков и углов геометрических фигур The formal normal form degenerate singular points in the case of case of focus
The formal normal form degenerate singular points in the case of case of focus