Содержание
- 2. ЗАДАЧА ЛІНІЙНОГО ПРОГРАМУВАННЯ ЗЛП є задачею знаходження найбільшого (чи найменшого) значення лінійної функції. Лінійне програмування -
- 3. Симплекс-метод — це поетапна обчислювальна процедура, в основу якої покладено принцип послідовного поліпшення значень цільової функції
- 4. Алгоритм розв'язування задачі лінійного програмування симплекс-методом складається з таких етапів: Визначення початкового опорного плану задачі лінійного
- 5. * вважати, що 1 мілілітр = 1 грам Визначити: 1) скільки філіжанок кожного виду кави необхідно
- 6. РОЗВ’ЯЗАННЯ ЗАДАЧІ
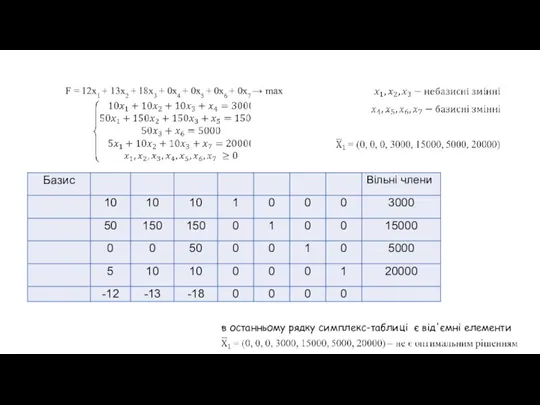
- 7. F = 12x1 + 13x2 + 18x3 + 0x4 + 0x5 + 0x6 + 0x7 →
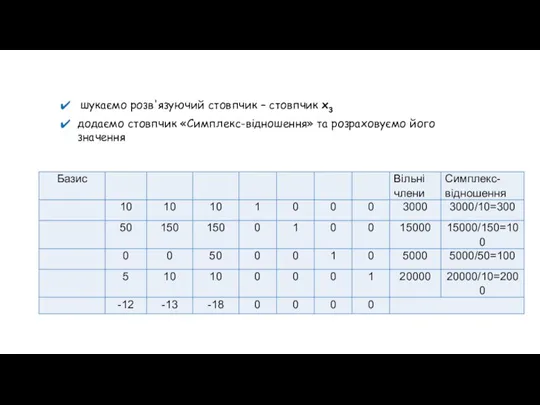
- 8. шукаємо розв'язуючий стовпчик – стовпчик x3 додаємо стовпчик «Симплекс-відношення» та розраховуємо його значення
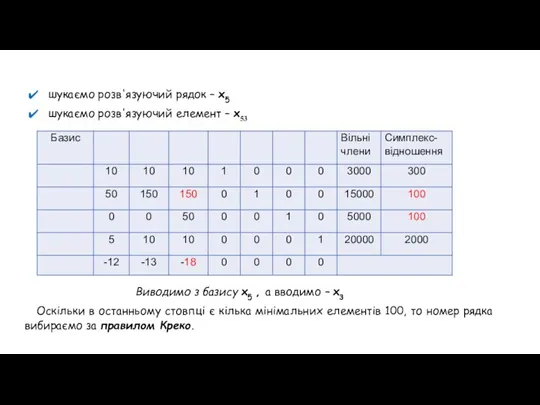
- 9. шукаємо розв'язуючий рядок – x5 шукаємо розв'язуючий елемент – x53 Виводимо з базису x5 , а
- 10. Елементи рядків, що мають однакові найменші значення (у нашому випадку min=100) , поділяються на передбачувані роздільники,
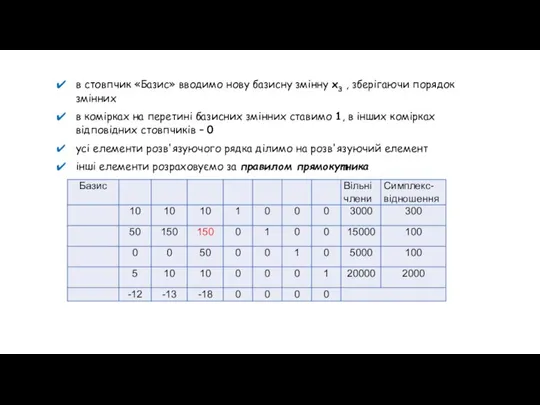
- 11. в стовпчик «Базис» вводимо нову базисну змінну x3 , зберігаючи порядок змінних в комірках на перетині
- 12. Уявно малюємо прямокутник, одна вершина якого збігається з розв'язуючим елементом, інша - з елементом, образ якого
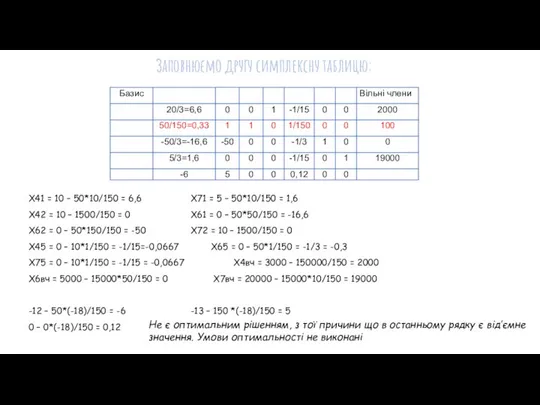
- 13. Заповнюємо другу симплексну таблицю: X41 = 10 – 50*10/150 = 6,6 X71 = 5 – 50*10/150
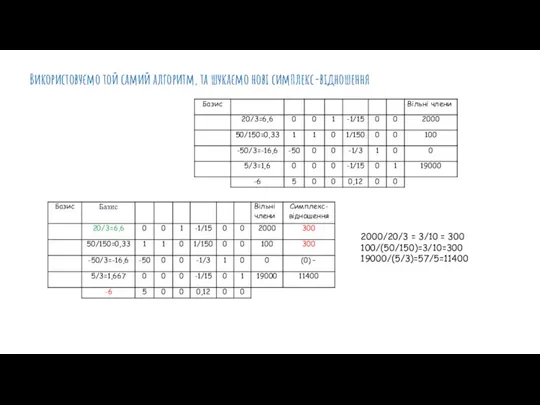
- 14. Використовуємо той самий алгоритм, та шукаємо нові симплекс-відношення 2000/20/3 = 3/10 = 300 100/(50/150)=3/10=300 19000/(5/3)=57/5=11400
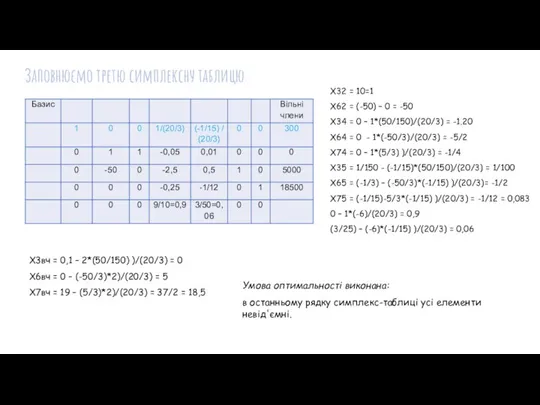
- 15. Заповнюємо третю симплексну таблицю: X32 = 10=1 X62 = (-50) – 0 = -50 X34 =
- 16. Отже, маємо таке оптимальне рішення:
- 17. У оптимальний план увійшла додаткова змінна x6. Отже, під час реалізації такого плану є недовикористані ресурси
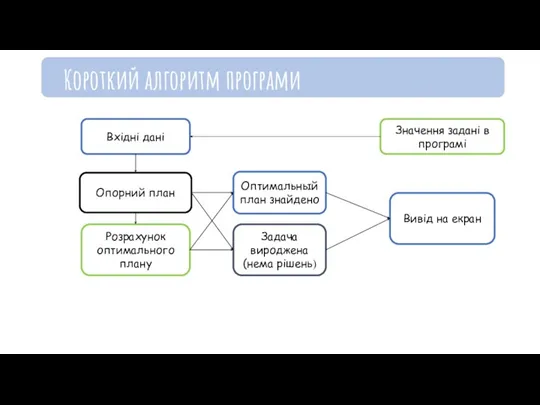
- 18. Вхідні дані Опорний план Розрахунок оптимального плану Задача вироджена (нема рішень) Оптимальный план знайдено Вивід на
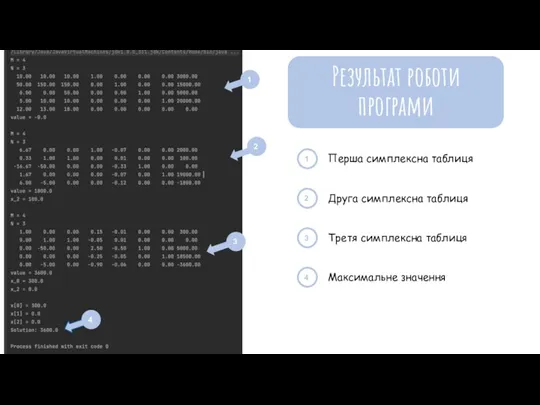
- 19. Результат роботи програми 1 4 2 1 2 3 Перша симплексна таблиця Друга симплексна таблиця Третя
- 20. РЕКОМЕНДАЦІЇ За даними умовами та обмеженнями максимальний виторг на день буде складати 3600 грн, та 79200
- 21. При виконанні даної лабораторної роботи, основна мета поставленого завдання була досягнута. Було вивчено базові завдання лінійного
- 23. Скачать презентацию










 Стохастические процессы
Стохастические процессы Презентация на тему Графическое решение уравнений
Презентация на тему Графическое решение уравнений  Старинные меры массы и длины
Старинные меры массы и длины Комплексные числа. Все формы
Комплексные числа. Все формы Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс
Развёртка параллелепипеда, куба, треугольной и четырёхугольной пирамиды. 5 класс Тригонометрические уравнения
Тригонометрические уравнения Квадратичная функция и её график. Методические материалы урока
Квадратичная функция и её график. Методические материалы урока Презентация на тему Объём многогранника
Презентация на тему Объём многогранника  Сближение меридианов. Международное геомагнитное аналитическое поле IGRF
Сближение меридианов. Международное геомагнитное аналитическое поле IGRF Задачи про форматы листов. Решение практико-ориентированных задач
Задачи про форматы листов. Решение практико-ориентированных задач Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Методика работы с задачей на круговое движение
Методика работы с задачей на круговое движение Основные формулы тригонометрии
Основные формулы тригонометрии Деление обыкновенных дробей
Деление обыкновенных дробей 7490_md_sin_cos_tg_0
7490_md_sin_cos_tg_0 Пирамида и её элементы. Правильная пирамида
Пирамида и её элементы. Правильная пирамида Математика вокруг нас
Математика вокруг нас Время. Единицы времени
Время. Единицы времени Первый замечательный предел
Первый замечательный предел Математика ЕГЭ. Углы и прямые
Математика ЕГЭ. Углы и прямые Линейная функция и её график
Линейная функция и её график Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Основы логистики
Основы логистики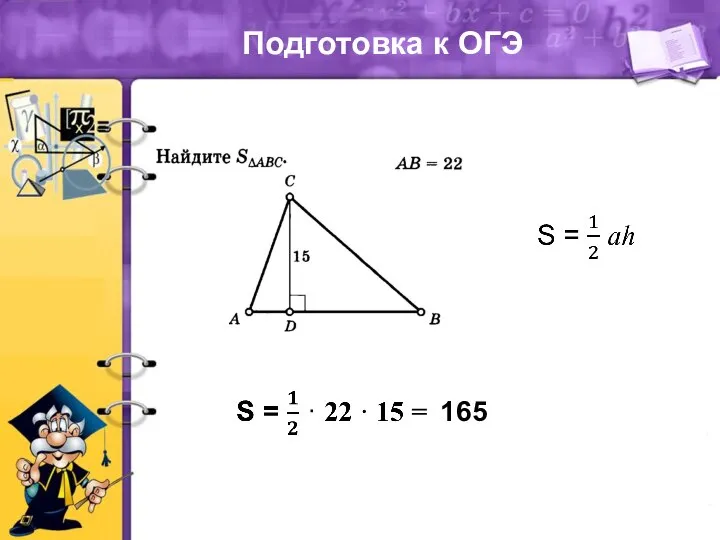 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Прямоугольник. Геометрия 8 класс
Прямоугольник. Геометрия 8 класс Логарифмические выражения
Логарифмические выражения Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -
Презентация по математике "Применение приёмов интерактивного обучения на уроках математики" -  Презентация на тему Метод координат в пространстве
Презентация на тему Метод координат в пространстве