Квадрат та його властивості

Мета уроку:
працювати над засвоєнням учнями змісту означень, властивостей та ознак квадрата. Формувати вміння відтворювати вивчені твердження; застосовувати властивості, ознаки квадрата до розв'язування типових задач.

Виконання усних вправ
Периметр ромба 24 см. Знайдіть сторони ромба.
Чи існує ромб зі стороною 10 см і діагоналями 6 см і 8 см? Відповідь обґрунтуйте.
У ромбі АВСD AD = 5см, DВ = 6 см, АС =8см. Знайдіть периметр ∆ВОС (О — точка перетину діагоналей).
Один з кутів між діагоналлю та стороною ромба дорівнює 72°. Знайдіть кути ромба.
У ромбі АВСD <А =32°. Знайдіть кути трикутника ВОС (О — точка перетину діагоналей).
6 см
Ні
12 см
144°; 108°; 144°; 108°
16°; 90°; 74°

Означення квадрата
Квадратом називають прямокутник, у якого всі сторони рівні.
Квадрат - паралелограм,
у якого сторони рівні,
тобто він є і ромбом.

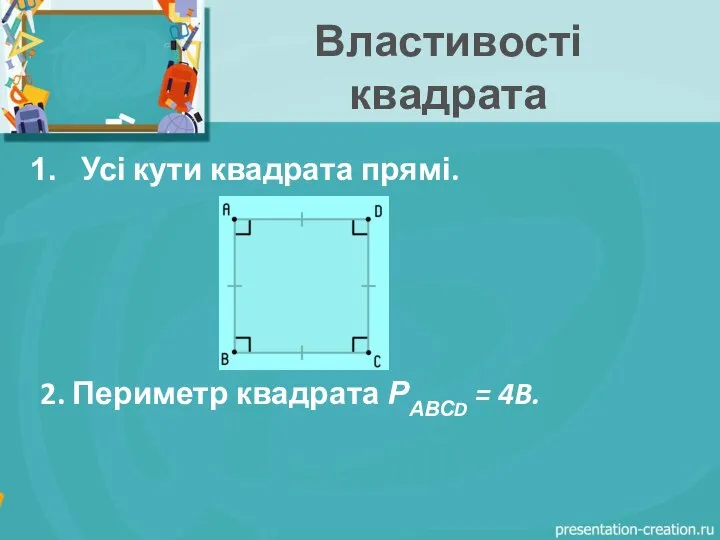
Властивості квадрата
Усі кути квадрата прямі.
2. Периметр квадрата РАВСD = 4B.

Властивості квадрата
3. Діагоналі квадрата між собою рівні.
BD = AC
4. Діагоналі квадрата взаємно перпендикулярні і точкою перетину діляться навпіл.
BO = ОD = AO = OС

Властивості квадрата
5. Діагоналі квадрата ділять його кути навпіл, тобто утворюють кути 45° зі сторонами квадрата.
6. Точка перетину діагоналей
квадрата рівновіддалена
від усіх його вершин:
АО = ВО = СО = DО.

Ознаки квадрата
Теорема (1 ознака квадрата). Якщо діагоналі прямокутника взаємно перпендикулярні, то він є квадратом.
Доведення. Прямокутник є паралелограмом, а паралелограм із взаємно перпендикулярними діагоналями є ромбом. Отже, у заданого прямокутника всі сторони рівні, а тому він є квадратом.

Ознаки квадрата
Теорема (2 ознака квадрата). Якщо діагоналі ромба між собою рівні, то він є квадратом.
Доведення. Ромб є паралелограмом, а паралелограм з рівними діагоналями є прямокутником. Отже, у розглядуваного ромба всі кути прямі, а тому він є квадратом.

Виконання усних вправ
Периметр квадрата дорівнює 20 см. Знайдіть його сторону.
Сторона квадрата дорівнює 7 дм. Знайдіть його периметр.
На малюнку зображено
квадрат ABCD. Назвіть рівні
між собою відрізки на
цьому малюнку.
5 см
28 дм

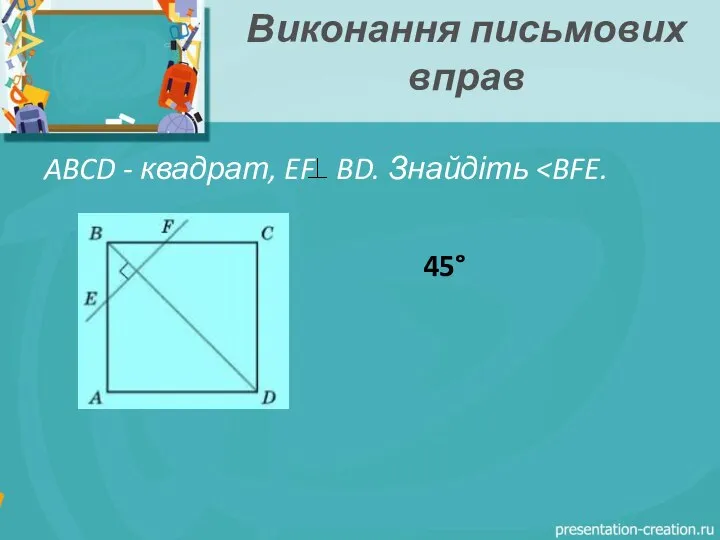
Виконання письмових вправ
ABCD - квадрат, EF BD. Знайдіть
45°

Виконання письмових вправ
Точка перетину діагоналей квадрата віддалена від його сторони на 3 см. Знайдіть периметр квадрата.
Р = 24 см

Підсумок уроку
Чи правильне твердження:
кожний квадрат є прямокутником;
існує квадрат, який не є ромбом;
кожний ромб є квадратом;
кожний квадрат є ромбом;
будь-який прямокутник є квадратом;
відношення периметра квадрата до його сторони є сталим для всіх квадратів?
так
ні
ні
ні
ні
так

Домашнє завдання
§ , №