Содержание
- 2. Немного из истории Квадратные уравнения в Древнем Вавилоне Необходимость решать уравнения не только первой, но и
- 3. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли
- 4. Теорема Виета Если приведенное квадратное уравнение x2+px+q=0 имеет действительные корни, то их сумма равна -p, а
- 5. Определение квадратного уравнения. Квадратным уравнением называется уравнение вида ax2+bx+c=0, где x - переменная, a, b, c
- 6. Решение примера.
- 8. Скачать презентацию





 Логарифмическая функция, ее свойства и график
Логарифмическая функция, ее свойства и график История развития квадратных уравнений
История развития квадратных уравнений Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Описательная статистика
Описательная статистика Соотношения между углами и сторонами треугольника
Соотношения между углами и сторонами треугольника Решение логических задач
Решение логических задач Математика ЕГЭ. Тригонометрические выражения. Часть 1
Математика ЕГЭ. Тригонометрические выражения. Часть 1 Случаи вычитания
Случаи вычитания Метод решения систем линейных уравнений методом Крамера
Метод решения систем линейных уравнений методом Крамера Прямая призма. Решение задач
Прямая призма. Решение задач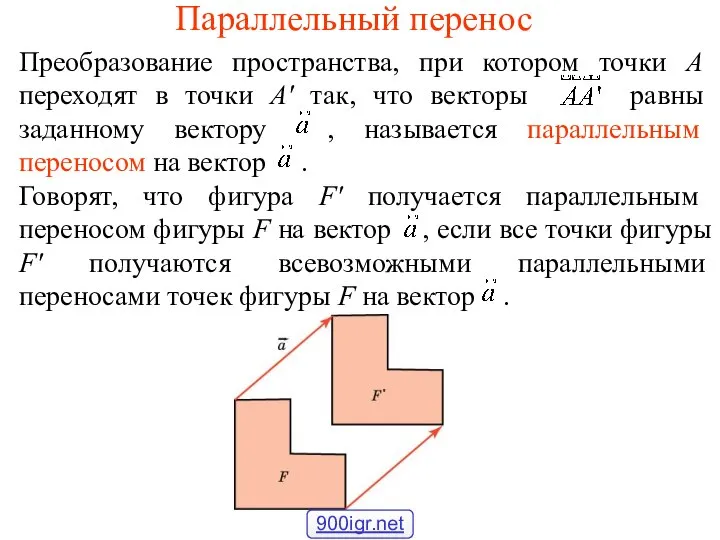 Параллельный перенос
Параллельный перенос Презентация на тему Тренажёр «Квадратные корни»
Презентация на тему Тренажёр «Квадратные корни» 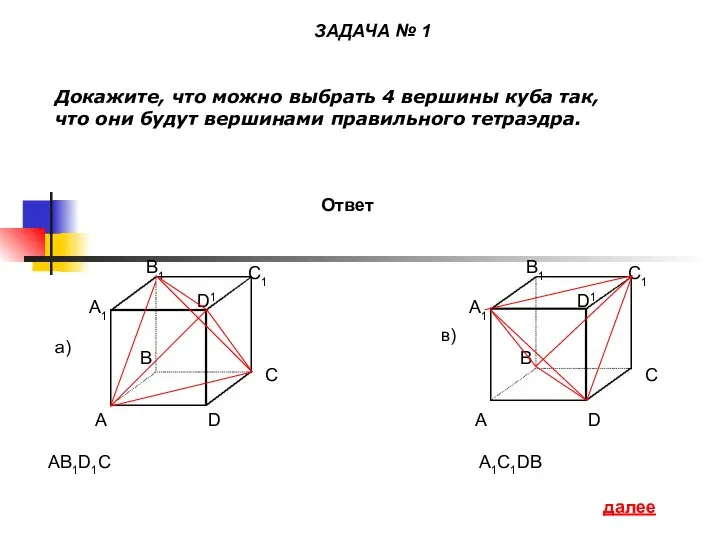 Задачи. Куб, тетраэдр
Задачи. Куб, тетраэдр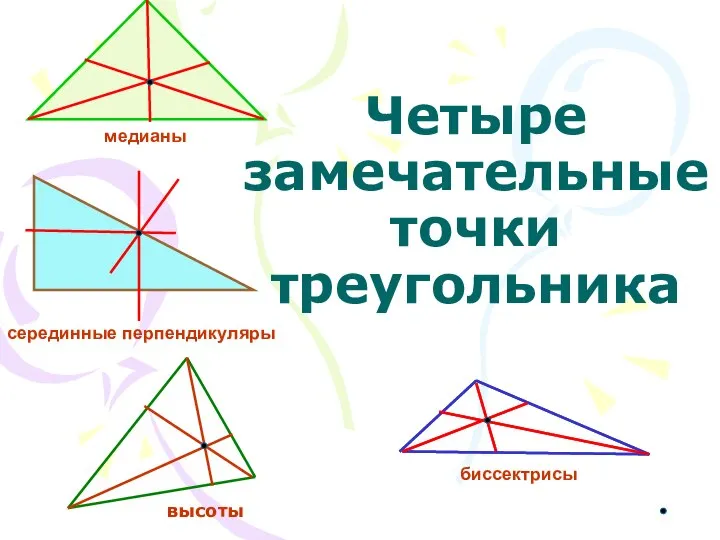 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Роль геометрии в изобразительном искусстве
Роль геометрии в изобразительном искусстве Вычисление длины дуги
Вычисление длины дуги Повторение курса алгебры за 10 класс
Повторение курса алгебры за 10 класс Математика в архитектуре
Математика в архитектуре Решение треугольников
Решение треугольников Решение задач
Решение задач Не итерируемые или неизменяемые объекты
Не итерируемые или неизменяемые объекты Формулы приведения
Формулы приведения Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Поворот. Типы вращений
Поворот. Типы вращений Числові нерівності. Властивості числових нерівностей
Числові нерівності. Властивості числових нерівностей Перпендикулярные прямые
Перпендикулярные прямые Деление на 2, 3, 4, 5 (повторение)
Деление на 2, 3, 4, 5 (повторение) Средства измерений, классификация. Метрологические характеристики средств измерений
Средства измерений, классификация. Метрологические характеристики средств измерений