Слайд 2«...и игры заслуживают изучения; и если какой-нибудь проницательный математик посвятит себя их

изучению, то получит много важных результатов, ибо нигде человек не показывает столько изобретательности, как в игре» .
Г. Лейбниц
Слайд 3Первый учебный вопрос:
Основные понятия теории игр

Слайд 4Применение теории игр
Нет математической теории, которая могла бы дать алгоритм любой реальной

игры, но существуют ситуации, подобные игровым и допускающие математический анализ.
Теория игр занимается изучением так называемых конфликтных ситуаций, где сталкиваются интересы индивидов, партий, государств и т. п.
Конфликтной называется ситуация, если в ней участвуют стороны, интересы которых полностью или частично противоположны.
Слайд 5Определение теории игр
Теорией игр называют научно обоснованные методы для рационального решения задач

с конфликтными ситуациями. Данные методы разработаны математической теорией конфликтных ситуаций.
Игра – это действительный или формальный конфликт, в котором имеется по крайней мере два участника (игрока), каждый из которых стремится к достижению собственных целей.
Правилами игры называются допустимые действия каждого из игроков, направленные на достижение некоторой цели.
Слайд 6Классификация игр
Интересы участников игры (игроков) могут оказаться несовпадающими и даже противоположными. В

последнем случае игра называется антагонистической.
В игре могут участвовать два и более игроков. Случай игры с одним участником (пасьянс, управление физическим объектом и т.д.) в сущности является игрой двух лиц, где вторым участником выступает природа (судьба, рок, провидение).
Игроки могут в игре выступать каждый за себя или объединяться в группы. В последнем случае игра называется коалиционной.
Слайд 7Классификация игр
Игра называется парной, если в ней участвуют два игрока, и множественной,

если число игроков больше двух. Далее будем рассматривать только парные игры. В такой игре участвуют два игрока - A и B, интересы которых противоположны. Под игрой (процессом игры) будет понимать ряд действий со стороны A и B.
Количественная оценка результатов игры называется платежом.
Слайд 8Классификация игр
Парная игра называется игрой с нулевой суммой, или антагонистической, если сумма

платежей равна нулю, т.е выигрыш одного игрока равен проигрышу другого. В этом случае для полного задания игры достаточно указать одну из величин. Если, например, a – выигрыш одного из игроков, b - выигрыш другого, то для игры с нулевой суммой b = -a, поэтому достаточно рассматривать, например, a.
Слайд 9Классификация игр
Игры, в которых игроки осведомлены о состоянии своем и партнеров, а

также о прошлом поведении участников игры, относятся к категории игр с полной информацией (шахматы, "крестики-нолики" и т.п.).
Большинство игр протекает в условиях неполной информации, где сведения о состоянии партнеров исчерпываются лишь вероятностными характеристиками (домино, карточные игры, игры против "природы").
Слайд 10Классификация игр
Выбор и осуществление одного из действий, предусмотренных правилами, называется ходом игрока.

Ходы могут быть личными и случайными.
Личный ход – это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре).
Случайный ход – это случайно выбранное действие (например, выбор карты из перетасованной колоды).
В дальнейшем мы будем рассматривать только личные ходы игроков.
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации.
Слайд 11Классификация игр
Каждая фиксированная стратегия игрока, где любой ситуации сопоставлен конкретный выбор, называется

чистой.
В реальности чаще используются так называемые смешанные стратегии, где чистые стратегии смешиваются с некоторыми частотами.
Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации. Однако, в принципе, возможно, что решения приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это означает, что игрок выбрал определенную стратегию, которая может быть задана в виде списка правил или программы.
Игра называется конечной, если у каждого игрока есть конечное число стратегий, и бесконечной – в противном случае.
Слайд 12Стратегия игрока называется оптимальной, если она обеспечивает игроку максимальный выигрыш (или, что

то же самое, минимальный проигрыш), при условии, что второй игрок придерживается своей стратегии.
Если игра повторяется много раз, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.
Для того чтобы решить игру, или найти решение игры, необходимо для каждого из игроков выбрать оптимальную стратегию.
Слайд 13Вывод
Таким образом, предмет теории игр составляют методы отыскания оптимальных стратегий игроков.
При

выборе оптимальной стратегии естественно предполагать, что оба игрока ведут себя разумно с точки зрения своих интересов.
Важнейшее ограничение теории игр - единственность выигрыша как показателя эффективности, в то время как в большинстве реальных экономических задач имеется более одного показателя эффективности. Кроме того, в экономике, как правило, имеют место задачи, в которых интересы партнеров не обязательно антагонистические. Однако решение игр при наличии многих участников, имеющих непротиворечивые интересы, - это гораздо более сложная задача.
Слайд 14Классификация игр
Простейшими являются игры 2 лиц с нулевой суммой.
Пусть в такой

игре игрок 1 имеет m выборов и игрок 2 - n выборов. Если игрок 1 делает свой i-й выбор, а игрок 2 - свой j-й выбор, то выигрыш игрока 1 (проигрыш игрока 2) равен Rij. Такая игра называется матричной и матрица R = [Rij / i=1..m , j=1..n] называется матрицей выигрышей (платежной матрицей).
При ведении игры игрок должен ориентироваться на оптимальную политику партнера и наказывать его за отступления от таковой.
Слайд 15Классификация игр
Проведем рассуждения за игрока 1. Если Я воспользуюсь i-м выбором, мой

противник для минимизации моего выигрыша сделает тот из своих выборов, который даст min Rij. Соответственно, Я должен использовать тот выбор, который гарантирует мне выигрыш, не меньший
Противник, рассуждая аналогично, приходит к выводу о гарантированном проигрыше, не превышающем
Слайд 16Классификация игр
Если в матрице выигрышей существует элемент Rkl=V1=V2, то говорят о наличии

оптимальной политики "в пространстве чистых стратегий" и оптимальными выборами для игроков соответственно являются выборы k и l. Пару (k,l) называют седловой точкой.
В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке.
Пример 1. Пусть игра определяется матрицей
Слайд 17Классификация игр
Седловые точки - (4,1) и (4,2). Цена игры = 6; оптимальный

выбор для игрока 1 - четвертый, для игрока 2 равнозначны первый и второй (под ценой игры понимают гарантированный выигрыш-проигрыш при оптимальной политике обоих игроков)
Слайд 18Классификация игр
Пример 2. Пусть игра определяется матрицей
Здесь равенство V1=V2 не выполняется; оптимальной

чистой стратегии для игроков нет.
Слайд 19Классификация игр
При анализе игр часто прибегают к попыткам обнаружить доминирование между строками

и столбцами. Так в примере 1 элементы четвертой строки больше элементов других строк: использование выбора 4 выгоднее других выборов при любой политике противника. Противник видит, что в такой ситуации использовать выборы 3 и 4 неразумно.
Использование доминирования таким образом позволяет уменьшить размеры изучаемой матрицы исключением "невыгодных" строк и столбцов.
При отсутствии седловой точки среди чистых стратегий приходится искать таковую среди смешанных.
Если игрок 1 прибегает к своему выбору i с вероятностью Pi, а игрок 2 - к своему j-му выбору с вероятностью Qj, то ожидаемый выигрыш игрока 1 (проигрыш игрока 2) равен
Слайд 20Классификация игр
Основная теорема теории игр (теорема Джона фон Неймана) утверждает, что любая

матричная игра с нулевой суммой всегда имеет седловую точку, т.е. существуют векторы P и Q такие, что
где V - цена игры.
Слайд 21Второй учебный вопрос:
Матричные игры и линейное программирование

Слайд 22Очевидно, что если игрок 1 отступит от оптимальной политики, а игрок 2

будет действовать оптимально, то выигрыш игрока 1 будет меньше цены игры, и если игрок 2 отступит от оптимальной политики при сохранении оптимального поведения игроком 1, то его проигрыш превысит цену игры:
Рассуждения игрока 1: мне хотелось бы максимизировать цену игры, т.е. мой гарантированный выигрыш, и я должен подобрать систему значений Pi так, чтобы при любом выборе противника мой ожидаемый выигрыш был больше цены игры.
Рассуждения игрока 2: мне хочется уменьшить мой гарантированный проигрыш, т.е. цену игры, и мне надо подобрать значения Qj так, чтобы при любом выборе противника мой проигрыш был меньше цены игры.
Слайд 23Отсюда возникают две задачи:
Легко показать, что эти задачи образуют пару двойственных задач

линейного программирования.
Таким образом, решение матричной игры сводится к решению пары двойственных линейных программ.
Слайд 24Обратим внимание на то, что при увеличении элементов матрицы R на любую

константу С цена игры увеличится на С и это изменение не окажет влияния на искомые вероятности выборов.
Таким образом, можно добиться, например, положительности элементов матрицы и, следовательно, цены игры. Поэтому можно допустить, что цена игры V положительна.
В предположении V > 0 проведем замену переменных
Хi = Pi / V; Yj = Qj / V.
Отсюда видно, что
Слайд 25Соответственно, поставленные задачи можно преобразовать к задачам с меньшим числом переменных:

Слайд 26Например, для игры с матрицей
возникают задачи:

Слайд 27Решение этих задач симплексным методом дает оптимальные значения
X = {11/37, 4/37,

5/37}, Y = {8/37, 7/37, 5/37}
и экстремумы целевых функций, равные 20/37.
Отсюда V = 37/20, P = {11/20, 4/20, 5/20}, Q = {8/20, 7/20, 5/20}.


























 Тест на распознавание предметов
Тест на распознавание предметов Брейн-ринг. Геометрия
Брейн-ринг. Геометрия Применение производной
Применение производной Иррациональные неравенства
Иррациональные неравенства Відео. Задача на 2 дії
Відео. Задача на 2 дії Оценка сложных систем в условиях неопределенности
Оценка сложных систем в условиях неопределенности Презентация на тему Графическое решение квадратных уравнений (8 класс)
Презентация на тему Графическое решение квадратных уравнений (8 класс)  Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе
Устные приёмы сложения и вычитания в пределах 100. Урок математики во 2 классе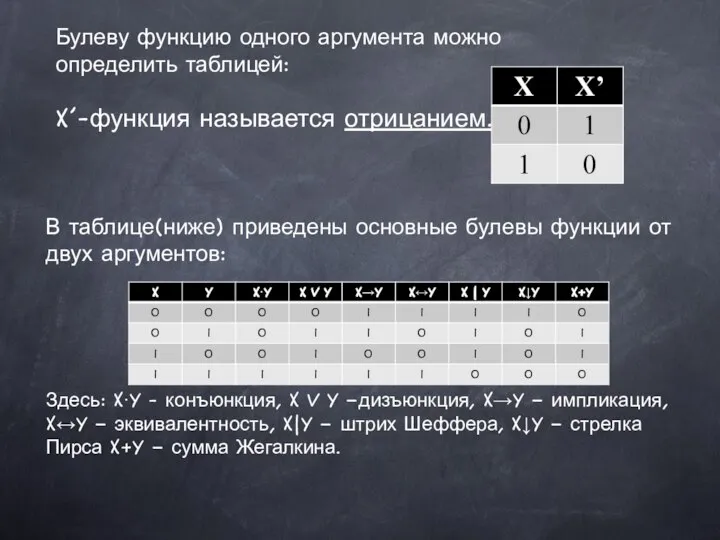 Булевы функции
Булевы функции Математический словарь
Математический словарь Презентация на тему Счет от одного до десяти
Презентация на тему Счет от одного до десяти  Золотое сечение в Web-дизайне
Золотое сечение в Web-дизайне Переменные. Арифметические операции
Переменные. Арифметические операции Вычисление углов между прямыми и плоскостями
Вычисление углов между прямыми и плоскостями Математика вокруг нас
Математика вокруг нас Граф. Построение графов
Граф. Построение графов ANX.ADJ.DSM.5
ANX.ADJ.DSM.5 Периметр и площадь прямоугольника. Подготовка к контрольной работе
Периметр и площадь прямоугольника. Подготовка к контрольной работе Числовые неравенства и их свойства. Подготовка к ОГЭ
Числовые неравенства и их свойства. Подготовка к ОГЭ Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах
Презентация на тему Использование игровых моментов при повторении на уроках математики в 5-ых классах  Презентация по математике "Познакомимся с известными математиками" -
Презентация по математике "Познакомимся с известными математиками" -  Наука эконометрика
Наука эконометрика Решение уравнений математической физики методом д’Аламбера
Решение уравнений математической физики методом д’Аламбера Определенный и неопред интеграл. Тема 8
Определенный и неопред интеграл. Тема 8 Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Интерактивный тест. Готовимся к ОГЭ. 2 вариант, задание 8
Интерактивный тест. Готовимся к ОГЭ. 2 вариант, задание 8 Геометрия на каждом уроке
Геометрия на каждом уроке Решение систем линейных уравнений разными методами
Решение систем линейных уравнений разными методами