Содержание
- 2. Основные элементарные функции: а) степенная: y = xn, n∈R; б) показательная: y = ax, a>0, a≠1;
- 3. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических операций (сложения, умножения, вычитания, деления,
- 4. АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ . Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). Алгебраической называется функция, в которой
- 5. РАЦИОНАЛЬНЫЕ ФУНКЦИИ . Алгебраические функции подразделяются на рациональные и иррациональные. Рациональными называются алгебраические функции, которые не
- 6. РАЦИОНАЛЬНЫЕ ФУНКЦИИ . Рациональные функции разделяются на целые рациональные функции (многочлены) и дробные рациональные (отношение многочленов).
- 7. Иррациональные функции . Иррациональными называются алгебраические функции, содержащие аргумент под знаком радикала (корня). Например,
- 8. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ . Трансцендентными (неалгебраическими) называют элементарные функции, которые не являются алгебраическими. (То есть, они образованы
- 9. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ . Замечание. Если вид элементарной функции можно упростить на всей области определения, то классификации
- 10. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ .
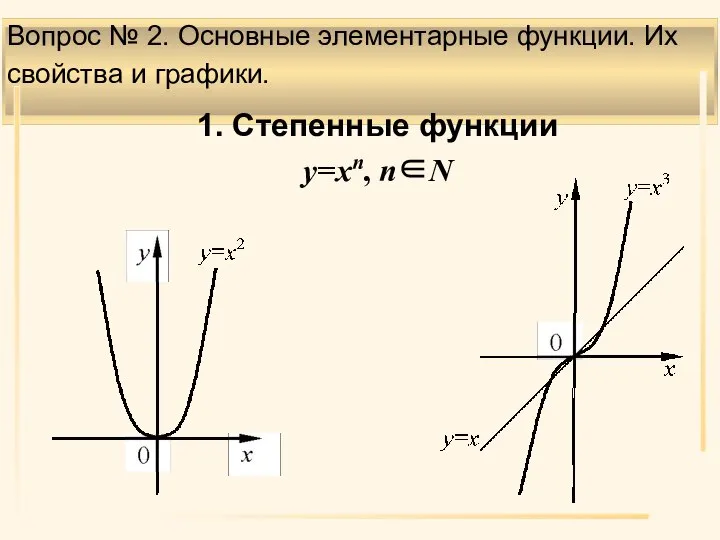
- 11. Вопрос № 2. Основные элементарные функции. Их свойства и графики. . 1. Степенные функции y=xn, n∈N
- 12. . Область определения Х: (–∞, ∞). Область значений Y: (–∞, ∞), если п – нечетно; [0,
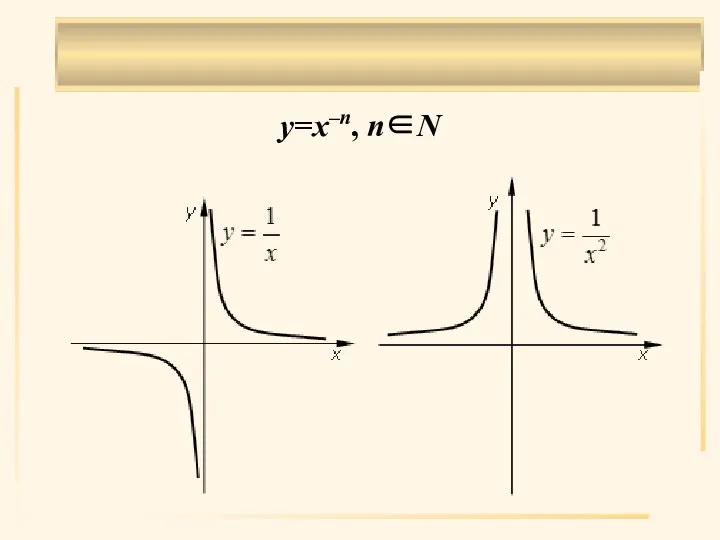
- 13. . y=x–n, n∈N
- 14. . Область определения X: (–∞, 0)∪(0,∞). Область значений Y: (–∞, 0)∪(0,∞), если п – нечетно; (0,
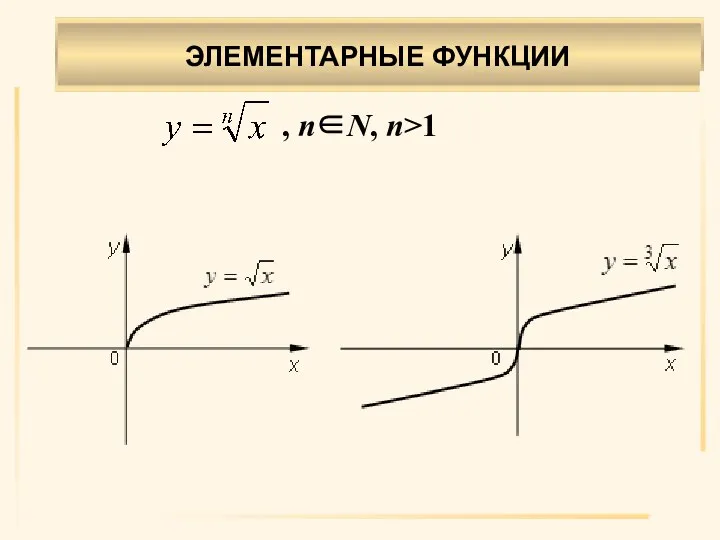
- 15. . , n∈N, n>1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- 16. . Область определения X: (–∞, ∞), если п – нечетно; [0, ∞), если п – четно.
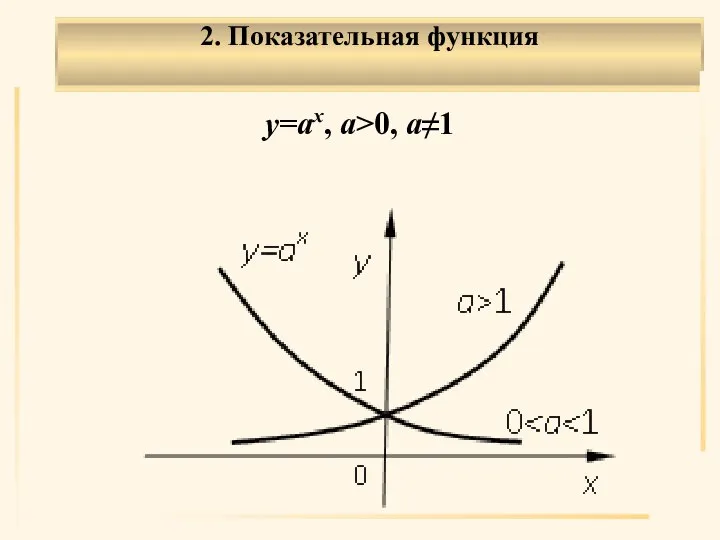
- 17. 2. Показательная функция . y=ax, a>0, a≠1
- 18. . Область определения X: (–∞, ∞). Область значений Y: (0, ∞). Общего вида. Возрастает на (–∞,
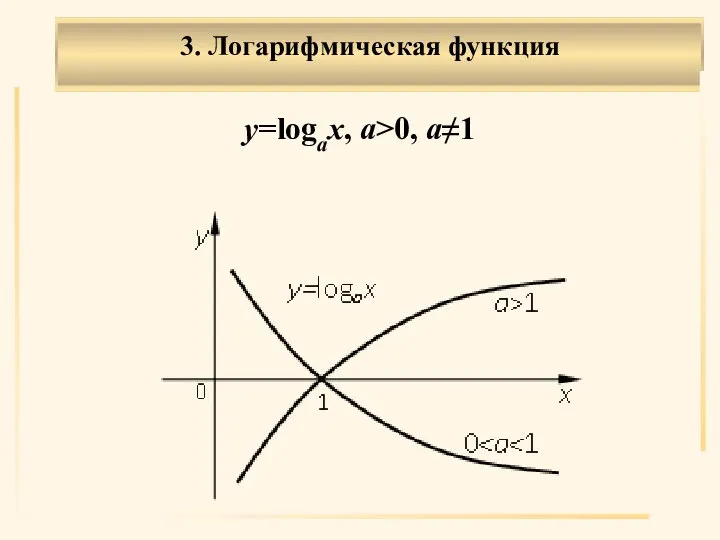
- 19. 3. Логарифмическая функция . y=logax, a>0, a≠1
- 20. . Область определения X: (0, ∞). Область значений Y: (–∞, ∞). Общего вида. Возрастает на (0,
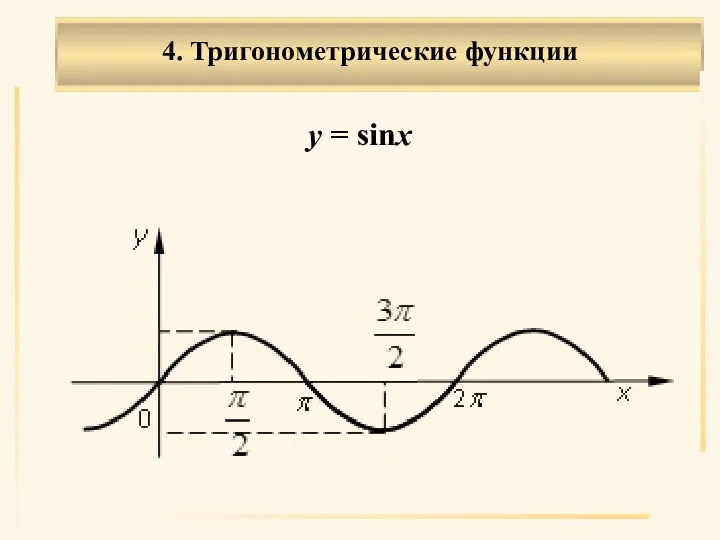
- 21. 4. Тригонометрические функции . у = sinx
- 22. . Область определения X: (–∞, ∞). Область значений Y: [–1, 1]. Нечетная. Возрастает на убывает на
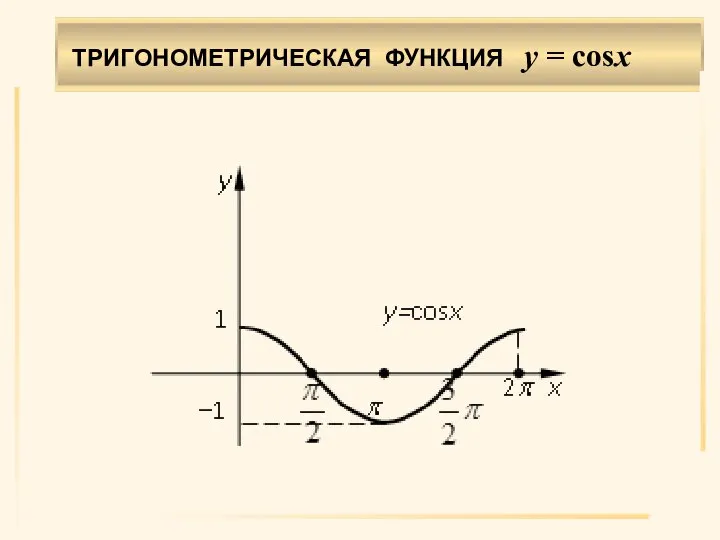
- 23. . ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ y = cosx
- 24. . Область определения X: (–∞, ∞). Область значений Y: [–1, 1]. Четная. Возрастает на убывает на
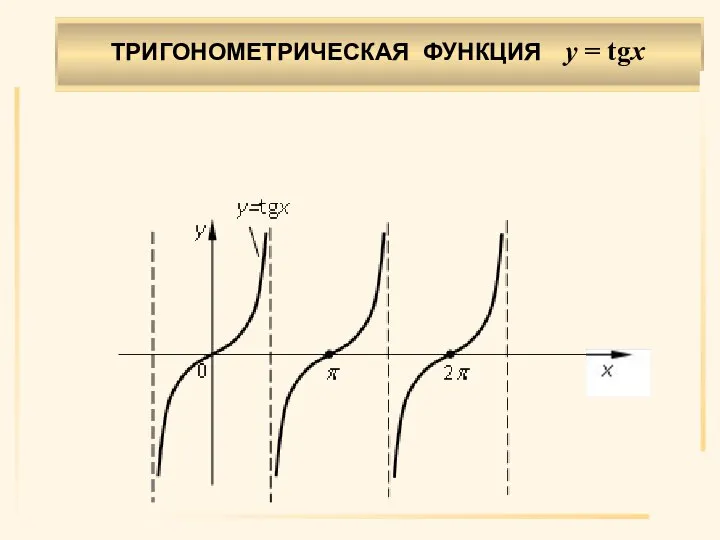
- 25. ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ y = tgx .
- 26. . Область определения X: , n∈Z. Область значений Y: (–∞, ∞). Нечетная. Возрастает на n∈Z. Период
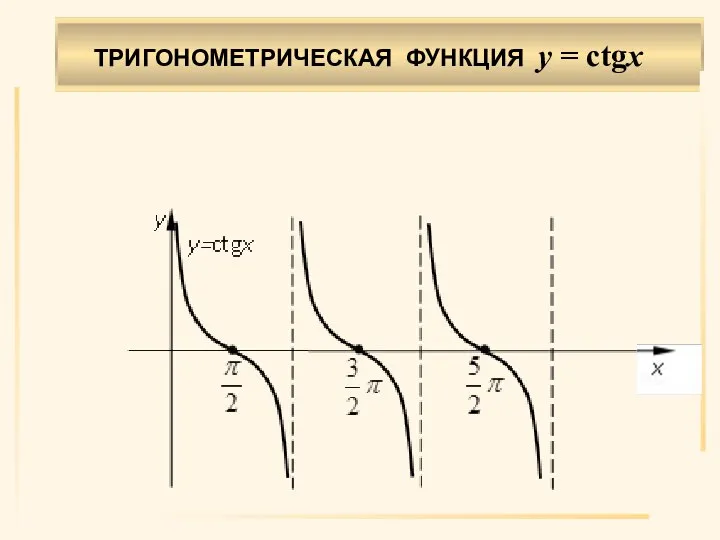
- 27. . ТРИГОНОМЕТРИЧЕСКАЯ ФУНКЦИЯ у = сtgx
- 28. . Область определения X: n∈Z. Область значений Y: [–∞, ∞). Нечетная. Убывает на n∈Z. Период π.
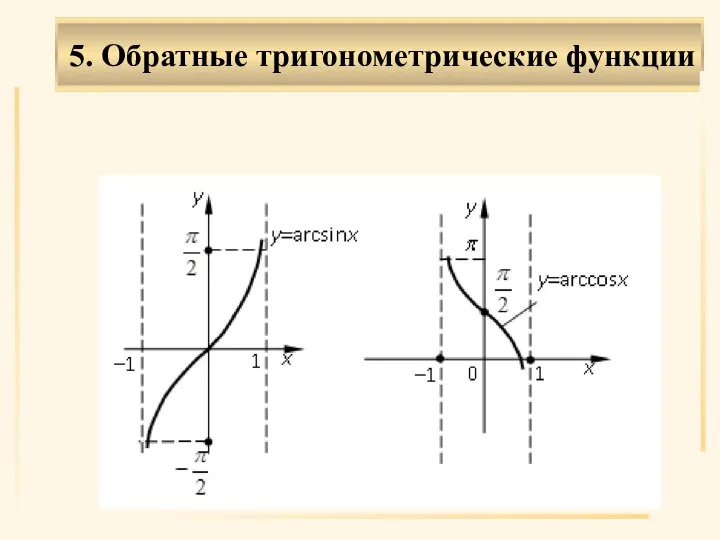
- 29. . 5. Обратные тригонометрические функции
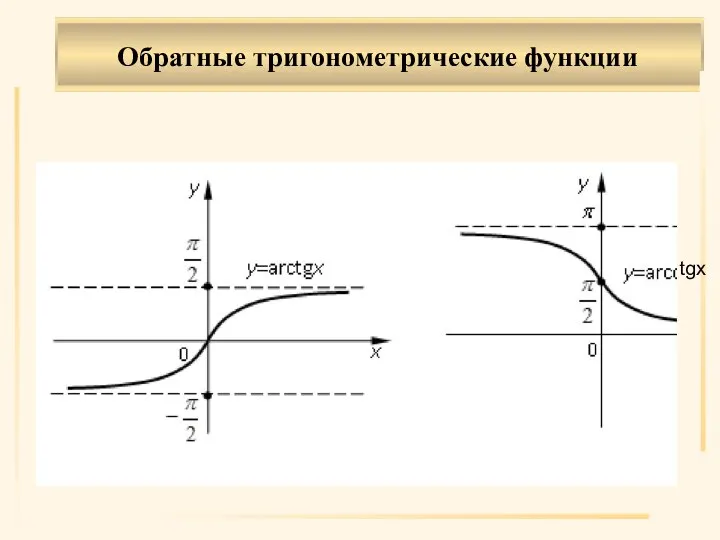
- 30. Обратные тригонометрические функции . tgх
- 31. . Области определения обратных тригонометрических функций: (|x|≤1), (–∞
- 33. Скачать презентацию














![. Область определения X: (–∞, ∞). Область значений Y: [–1, 1]. Нечетная.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1178819/slide-21.jpg)
![. Область определения X: (–∞, ∞). Область значений Y: [–1, 1]. Четная.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1178819/slide-23.jpg)



 Умножение обыкновенных дробей
Умножение обыкновенных дробей Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1
Исторические задачи комбинаторики и теории вероятностей. Самостоятельная внеаудиторная работа 1 Механический смысл производной. Задания для устного счета
Механический смысл производной. Задания для устного счета Анализ и синтез. 58-59-60 Урок
Анализ и синтез. 58-59-60 Урок Решение задач на проценты
Решение задач на проценты Оценка качества регрессии. Автокорреляция остаточной компоненты модели
Оценка качества регрессии. Автокорреляция остаточной компоненты модели Путешествие в историю математики. Решение старинных задач
Путешествие в историю математики. Решение старинных задач Площади четырёхугольников. Решение задач
Площади четырёхугольников. Решение задач Осевая симметрия
Осевая симметрия Случаи сложения вида +5
Случаи сложения вида +5 Непрерывность функции
Непрерывность функции Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения  Прямые на плоскости
Прямые на плоскости Уравнения фигур
Уравнения фигур Решение задач
Решение задач Ch3-Determinants
Ch3-Determinants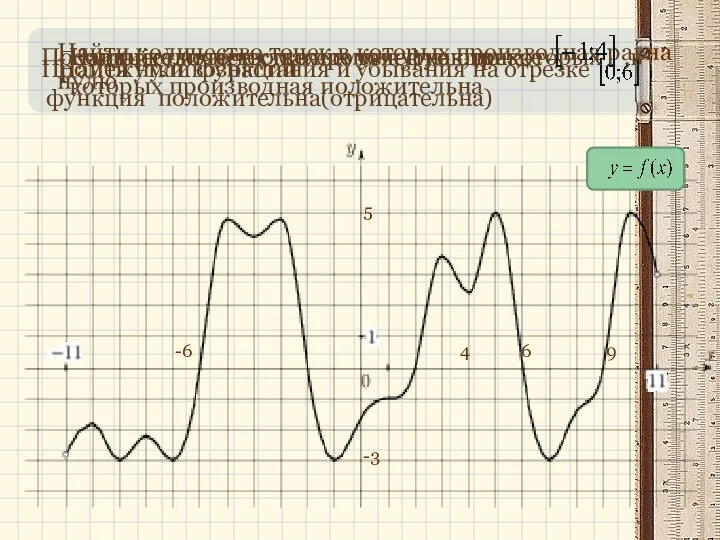 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Проценты
Проценты Решение уравнения в 1классе
Решение уравнения в 1классе Прямая на плоскости
Прямая на плоскости Математика (1 класс)
Математика (1 класс) Метод координат на плоскости
Метод координат на плоскости Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Угол между векторами (часть 2)
Угол между векторами (часть 2) Векторы. Действия с векторами
Векторы. Действия с векторами Сказ о дележе наследства (задача)
Сказ о дележе наследства (задача) Производная вокруг нас
Производная вокруг нас Пересечение поверхностей
Пересечение поверхностей