Содержание
- 2. Цель работы: Развитие пространственных представлений. Задачи: Познакомить с правилами построения сечений. Выработать навыки построения сечений тетраэдра
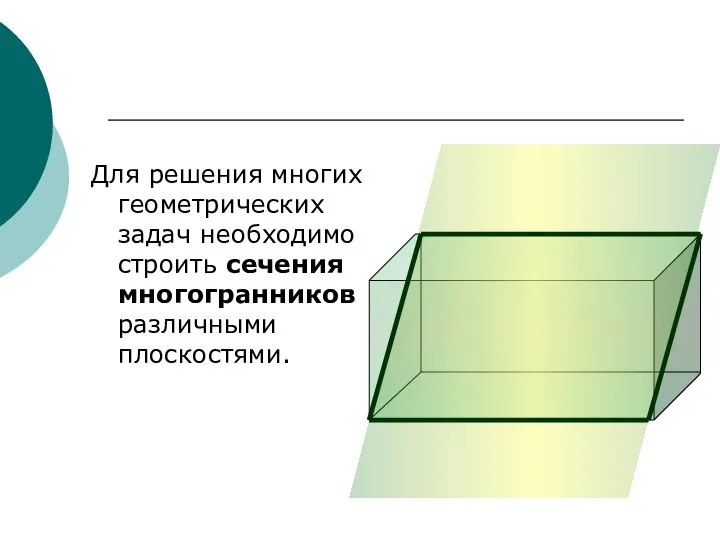
- 3. Для решения многих геометрических задач необходимо строить сечения многогранников различными плоскостями.
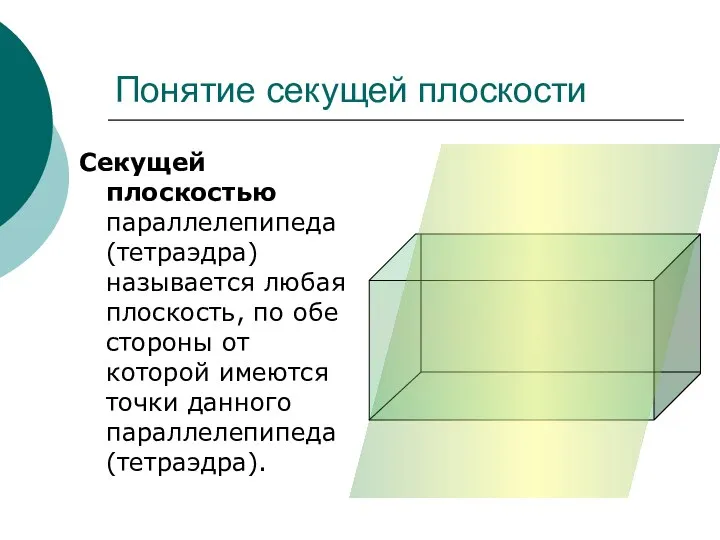
- 4. Понятие секущей плоскости Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны от которой имеются
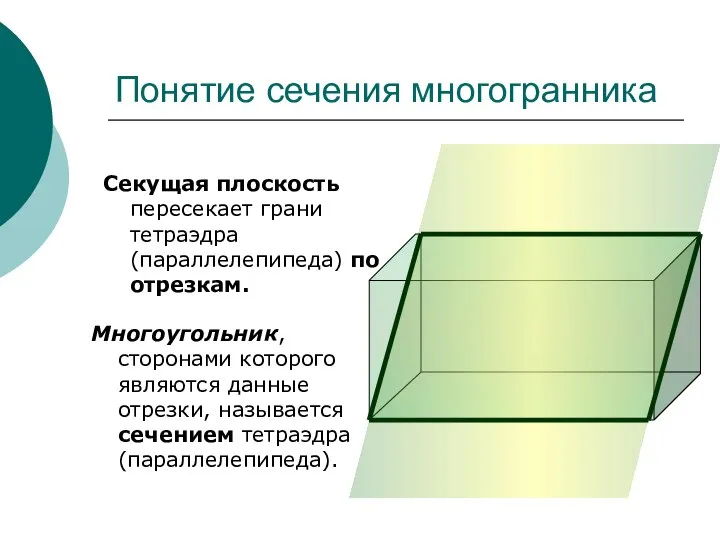
- 5. Многоугольник, сторонами которого являются данные отрезки, называется сечением тетраэдра (параллелепипеда). Понятие сечения многогранника Секущая плоскость пересекает
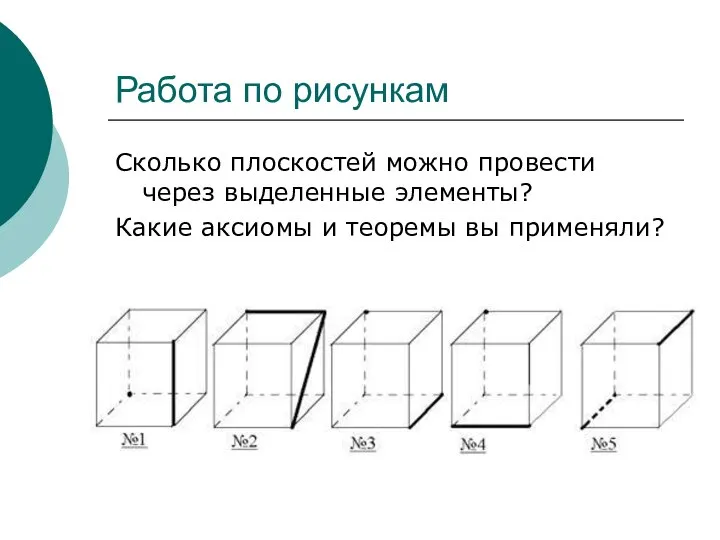
- 6. Работа по рисункам Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли?
- 7. Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
- 8. 1. Соединять можно только две точки, лежащие в плоскости одной грани. 2. Секущая плоскость пересекает параллельные
- 9. 3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную
- 10. Построение сечений тетраэдра
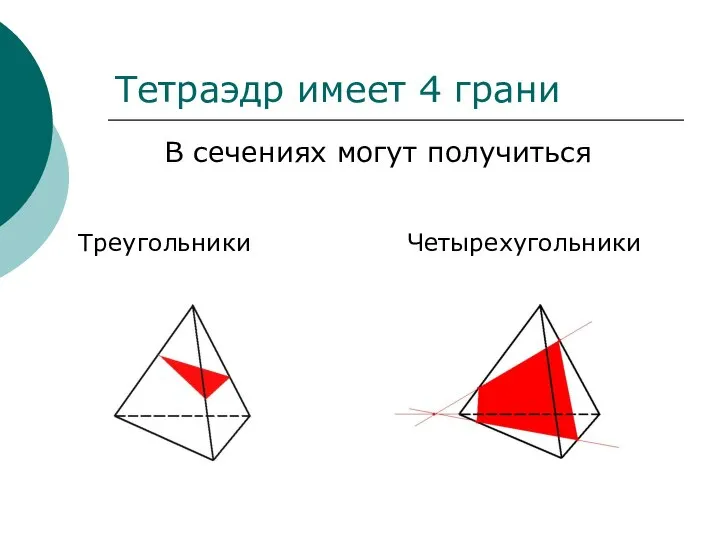
- 11. В сечениях могут получиться Четырехугольники Треугольники Тетраэдр имеет 4 грани
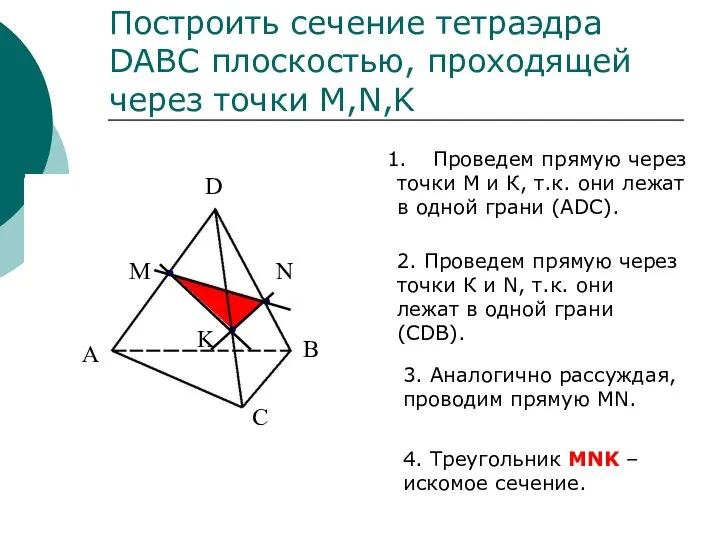
- 12. Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K Проведем прямую через точки М и К,
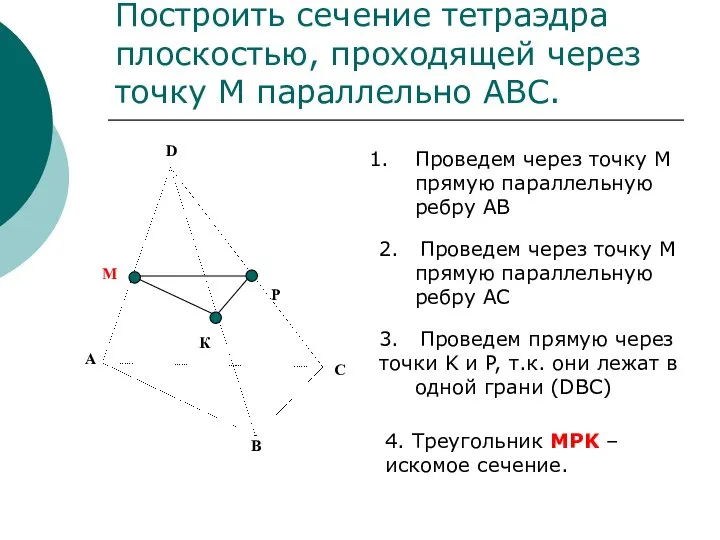
- 13. Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно АВС. Проведем через точку М прямую параллельную
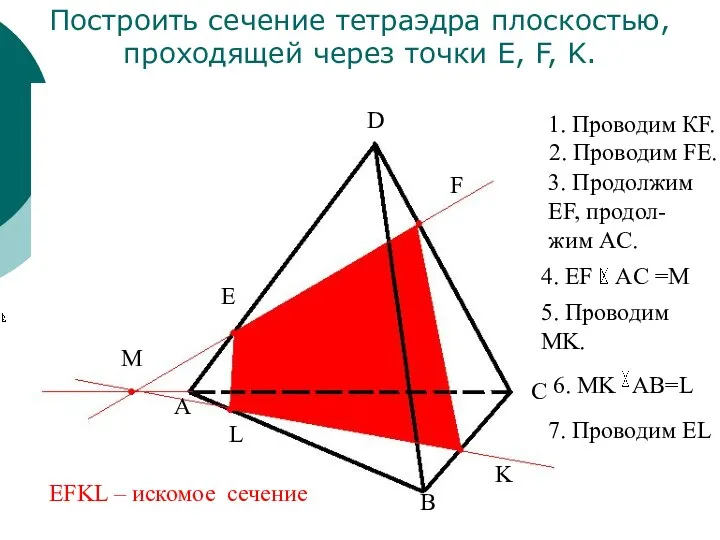
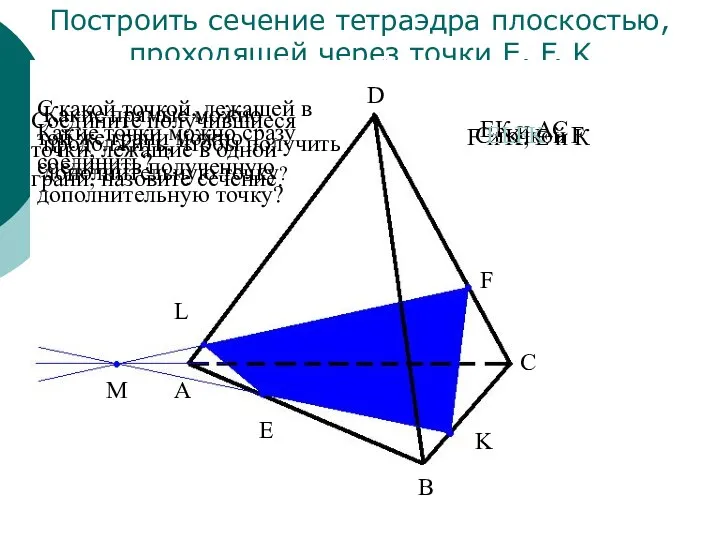
- 14. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K. E F K L A B
- 15. Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K E F K L A B
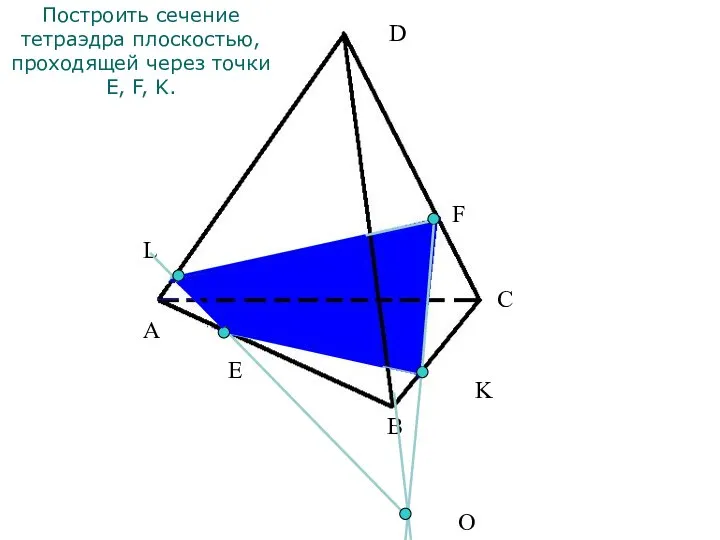
- 16. E F L A B C D О Построить сечение тетраэдра плоскостью, проходящей через точки E,
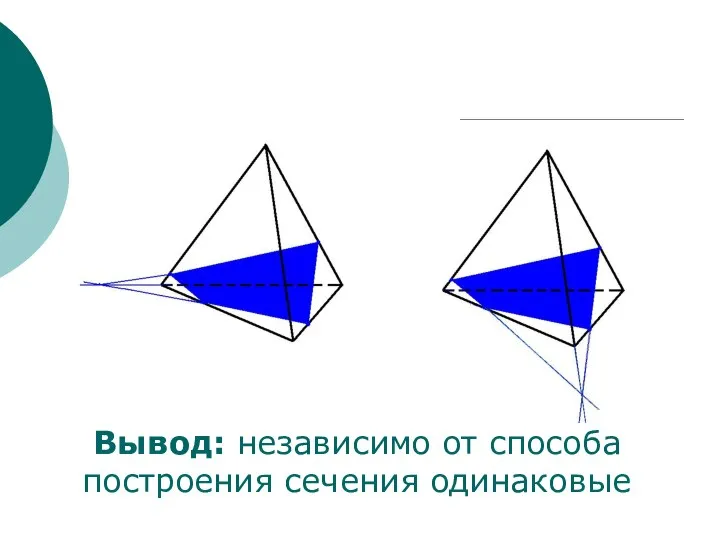
- 17. Вывод: независимо от способа построения сечения одинаковые
- 18. Построение сечений параллелепипеда
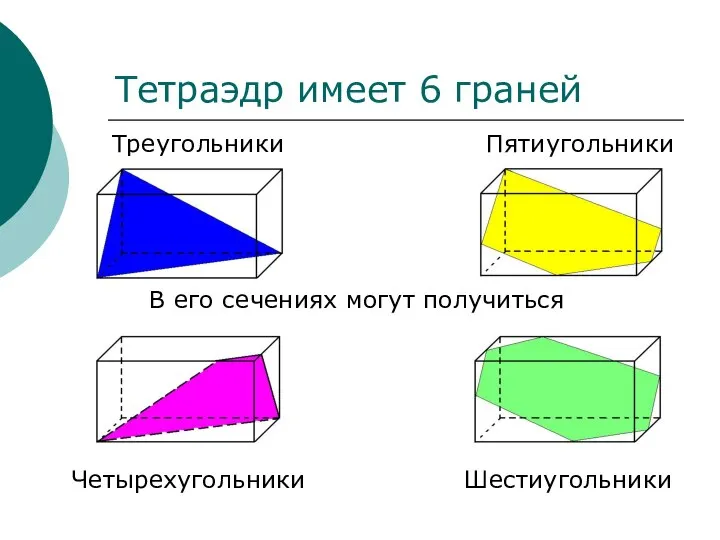
- 19. В его сечениях могут получиться Тетраэдр имеет 6 граней
- 20. Построить сечение параллелепипеда плоскостью проходящей через точку Х параллельно плоскости (ОСВ) 2. Через точку X прямую
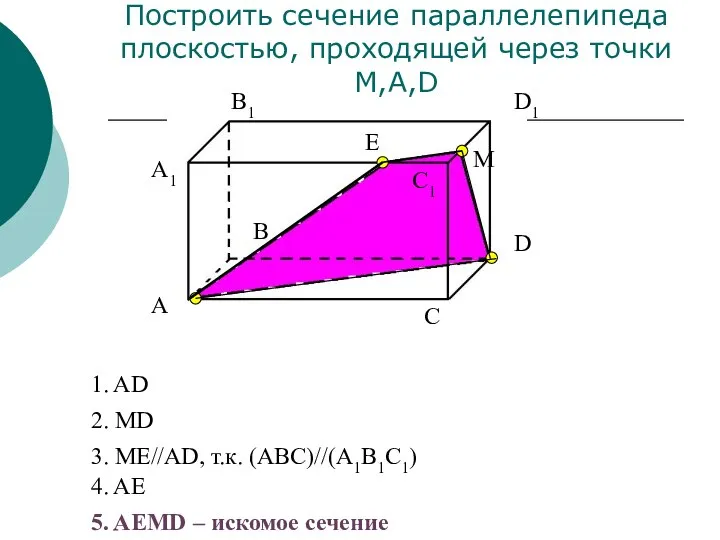
- 21. A1 А В В1 С С1 D D1 Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D
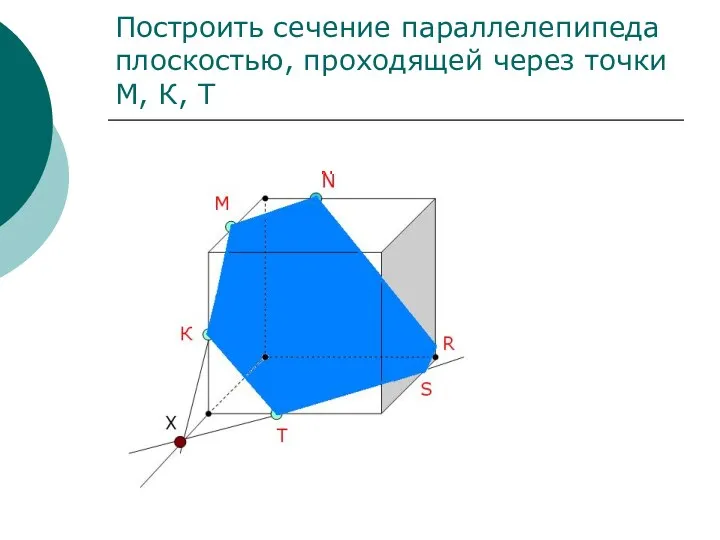
- 22. Построить сечение параллелепипеда плоскостью, проходящей через точки М, К, Т М К Т
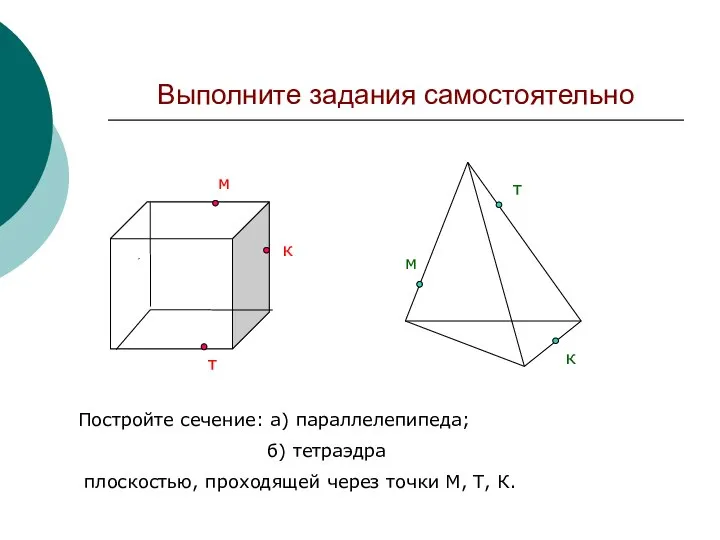
- 23. Выполните задания самостоятельно Д м к т м к т Постройте сечение: а) параллелепипеда; б) тетраэдра
- 25. Скачать презентацию







 Презентация на тему Вертикальные и смежные углы
Презентация на тему Вертикальные и смежные углы  Свойства показательной функции
Свойства показательной функции Элементы комбинаторики
Элементы комбинаторики Прямоугольный параллелепипед. Многогранники
Прямоугольный параллелепипед. Многогранники Daļas atņemšana no veselā
Daļas atņemšana no veselā Округление десятичных дробей. Опорные конспекты
Округление десятичных дробей. Опорные конспекты Число и цифра 2
Число и цифра 2 Пирамида. Виды пирамид
Пирамида. Виды пирамид Проценты
Проценты Круг, окружность, длина окружности. 6 класс
Круг, окружность, длина окружности. 6 класс Lektsia-2-russ
Lektsia-2-russ Упрощение выражений. Тест
Упрощение выражений. Тест Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Площадь и объём фигуры
Площадь и объём фигуры Геомет.1
Геомет.1 Методы теории вероятностей и математической статистики в выборе фильма
Методы теории вероятностей и математической статистики в выборе фильма Презентация на тему Признаки делимости от 2 до 15
Презентация на тему Признаки делимости от 2 до 15  Решение тригонометрических уравнений уравнения, сводящиеся к алгебраическим
Решение тригонометрических уравнений уравнения, сводящиеся к алгебраическим Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс)
Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых (4 класс) Движение в математике
Движение в математике Многочлены. Обобщающий урок - путешествие
Многочлены. Обобщающий урок - путешествие Текстовые задачи. Задание №1
Текстовые задачи. Задание №1 Производные и первообразные 1
Производные и первообразные 1 Признаки возрастания и убывания функции. Экстремум функции
Признаки возрастания и убывания функции. Экстремум функции Презентация на тему Одночлен
Презентация на тему Одночлен  Деление с остатком
Деление с остатком Мир функций и графиков. Урок - аукцион
Мир функций и графиков. Урок - аукцион Математика. Решение задач
Математика. Решение задач