Скрещивающиеся прямые

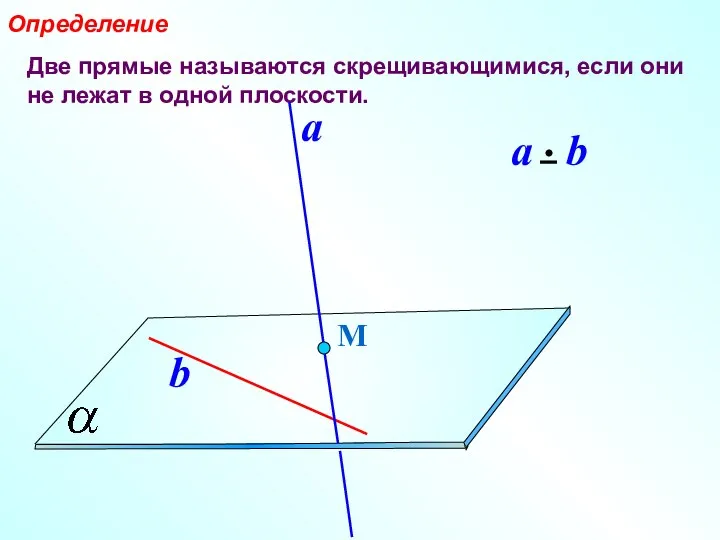
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Определение
М
a
b

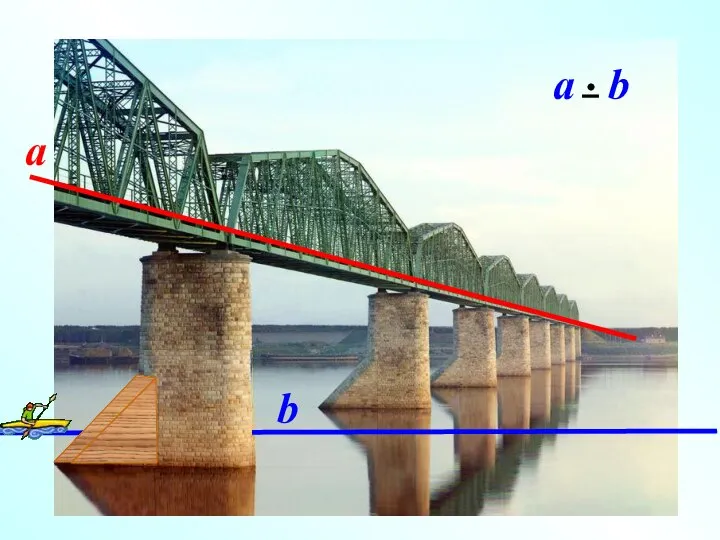
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi
Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.

a
b

Найдите на рисунке параллельные прямые.
Назовите параллельные прямые и плоскости.
Найдите скрещивающиеся прямые.

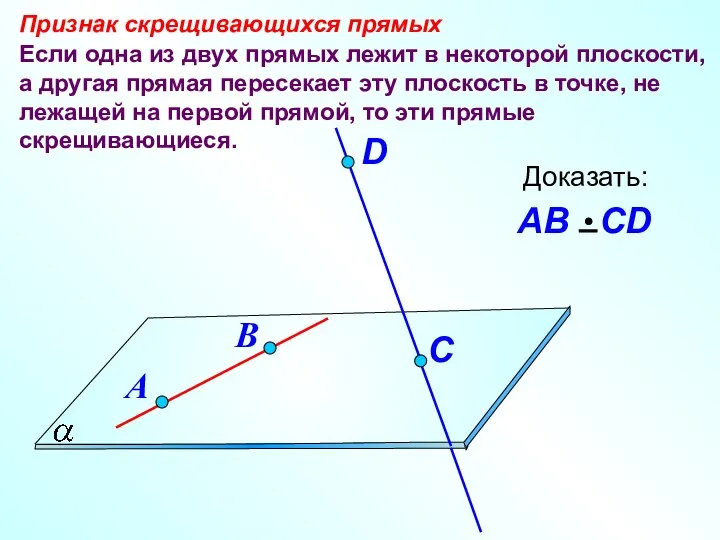
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Признак скрещивающихся прямых
D
В
А
C
Доказать:

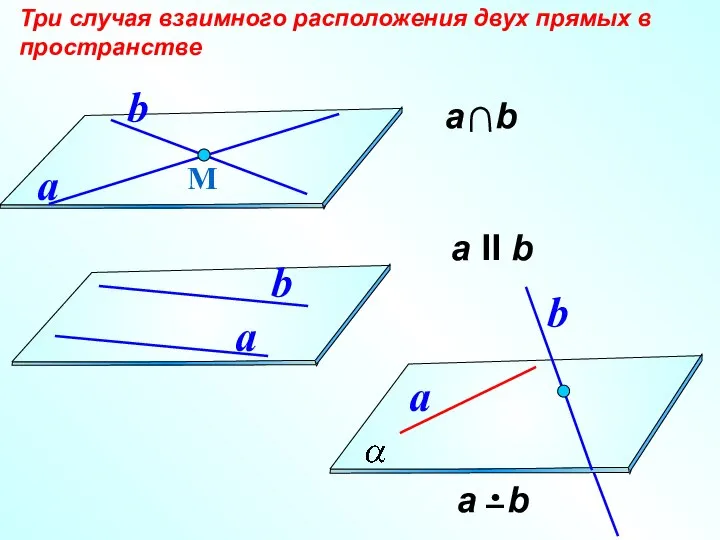
а II b
Три случая взаимного расположения двух прямых в пространстве
М
a
b
a
b
a
b

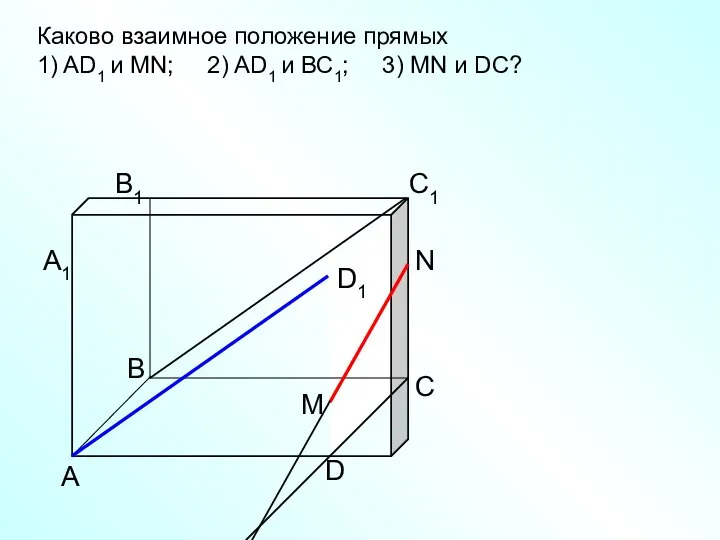
А
D
С
В
B1
С1
D1
А1
Каково взаимное положение прямых
1) AD1 и МN; 2) AD1 и ВС1; 3) МN и DC?
N
M

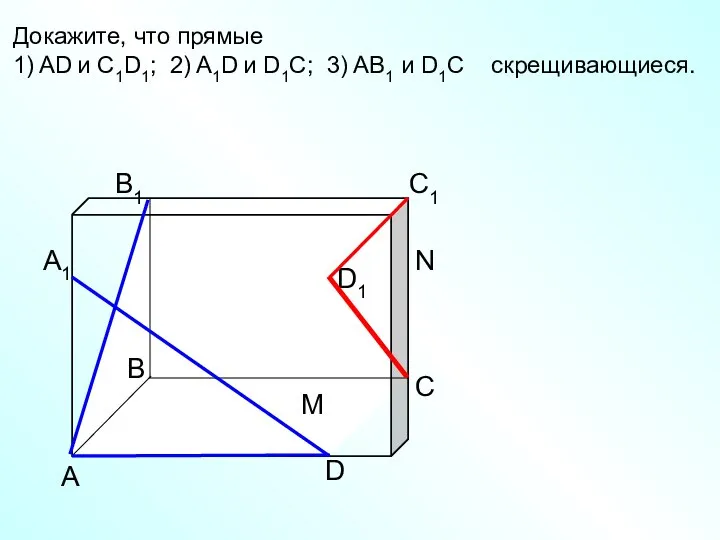
А
D
С
В
B1
С1
D1
А1
Докажите, что прямые
1) AD и C1D1; 2) A1D и D1C; 3) AB1 и D1C скрещивающиеся.
N
M

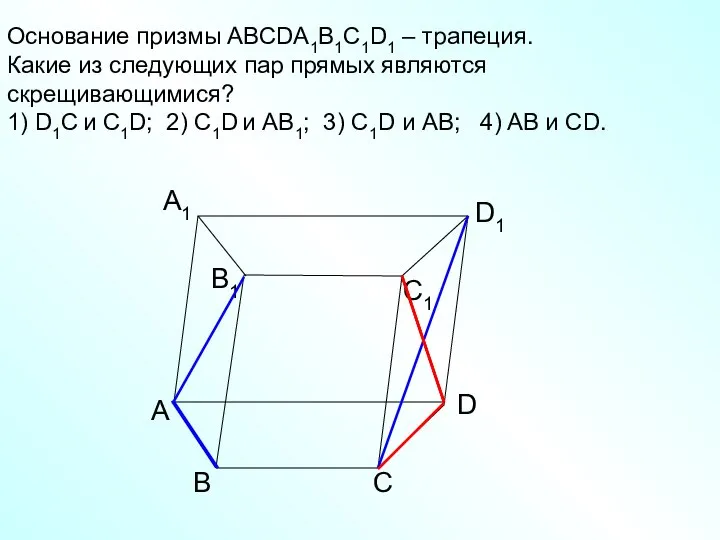
А
D
С
В
B1
С1
D1
А1
Основание призмы АВСDA1B1C1D1 – трапеция.
Какие из следующих пар прямых являются
скрещивающимися?
1) D1C и C1D; 2) C1D и AB1; 3) C1D и AB; 4) AB и CD.

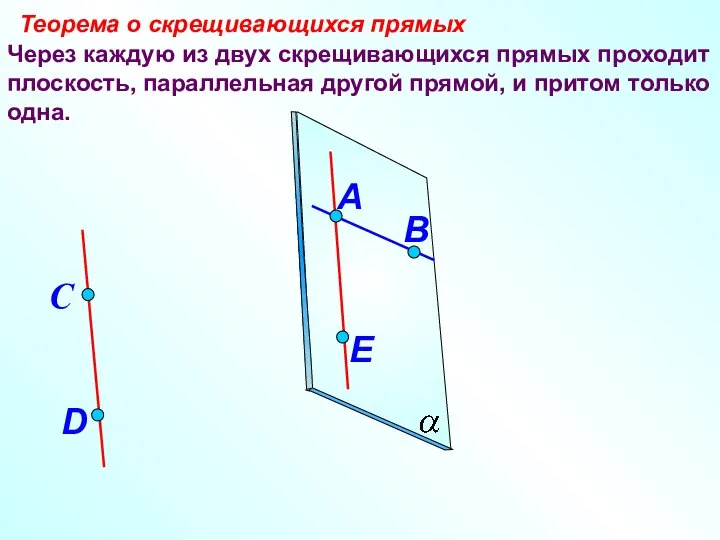
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Теорема о скрещивающихся прямых
D
С
B
A