Содержание
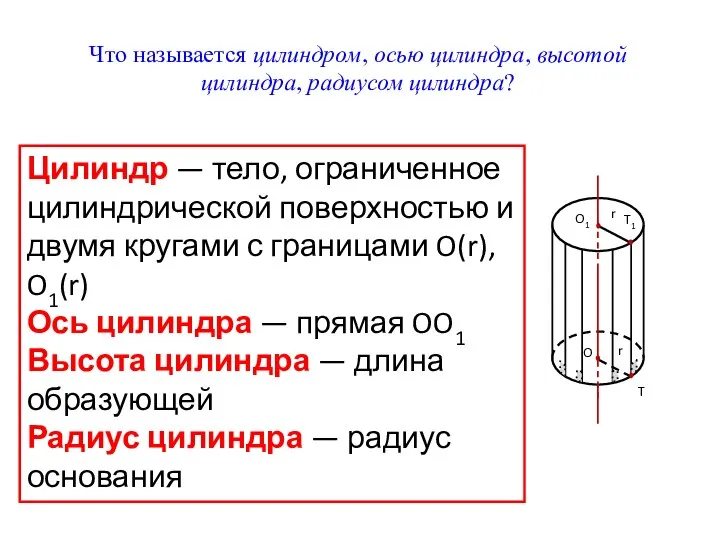
- 2. Что называется цилиндром, осью цилиндра, высотой цилиндра, радиусом цилиндра? O r O1 r T1 T Цилиндр
- 3. Теорема Объём цилиндра равен произведению площади основания на высоту V = πr2h Теорема Объём цилиндра равен
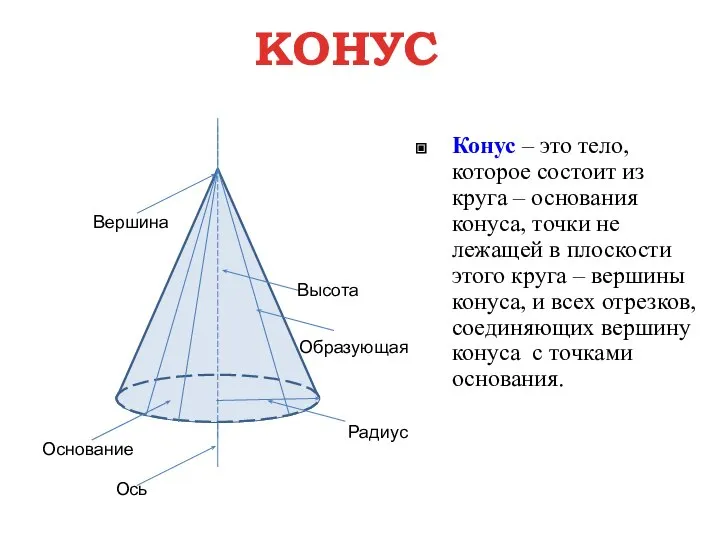
- 4. КОНУС Высота Образующая Радиус Вершина Ось Основание Конус – это тело, которое состоит из круга –
- 5. Конус – тело вращения… Конус можно получить путем вращения прямоугольного треугольника вокруг одного из его катетов.
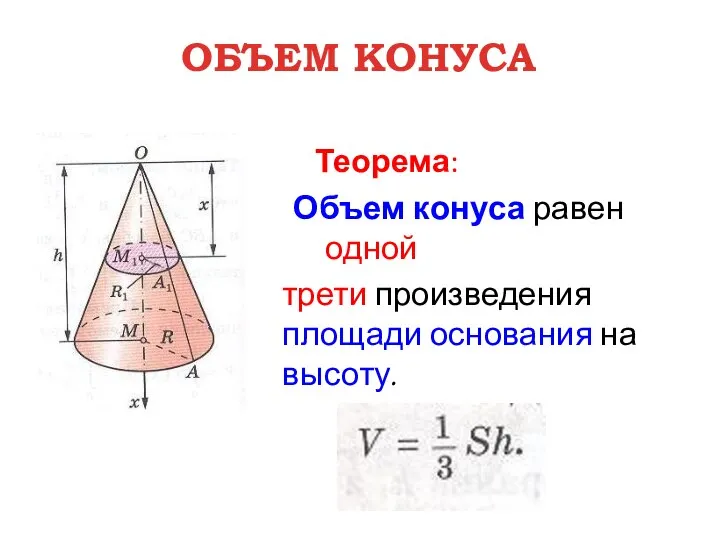
- 6. ОБЪЕМ КОНУСА Теорема: Объем конуса равен одной трети произведения площади основания на высоту.
- 7. Объём усеченного конуса Следствие: Объем усеченного конуса, высота которого равна h, а площадь оснований S и
- 8. Объем усеченного конуса, основания которого – круги радиусов R и r, а высота равна h, выражается
- 9. Решение задач
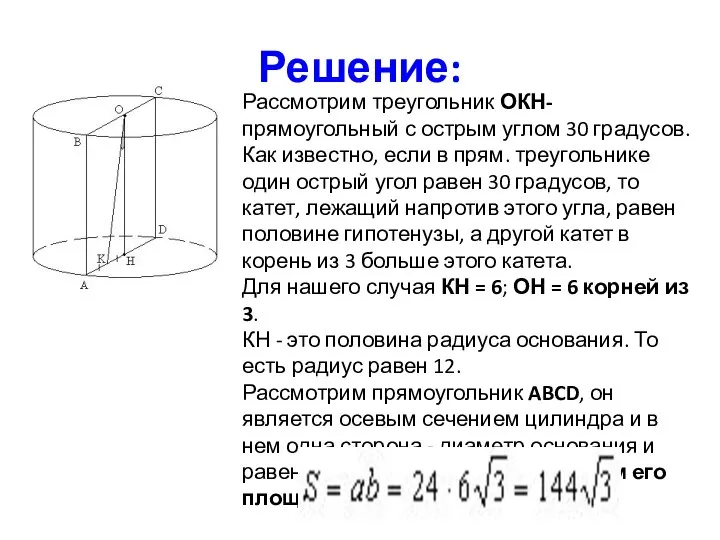
- 10. Задача 1. Отрезок, соединяющий центр верхнего основания цилиндра с серединой радиуса нижнего основания, равен 12см. и
- 11. Решение: Рассмотрим треугольник ОКН- прямоугольный с острым углом 30 градусов. Как известно, если в прям. треугольнике
- 12. Решение: Теперь найдем объём цилиндра и площадь полной поверхности:
- 13. Задача 2. Осевое сечение цилиндра прямоугольник со сторонами 8 и 12 дм. Найти объём цилиндра и
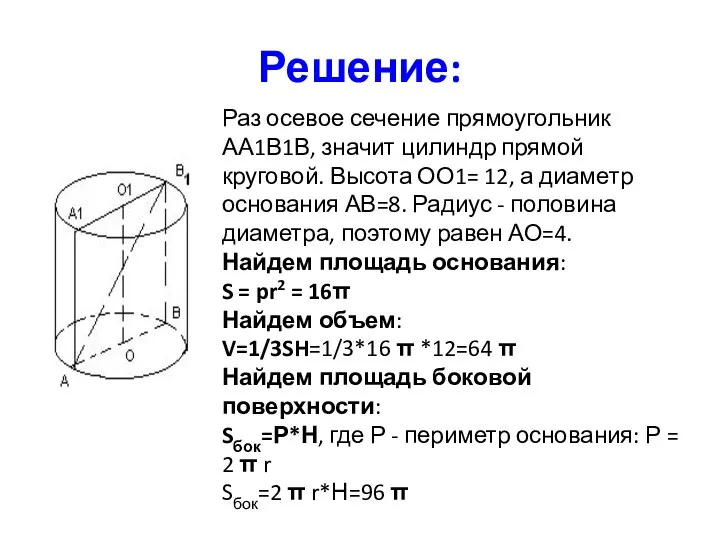
- 14. Решение: Раз осевое сечение прямоугольник АА1В1В, значит цилиндр прямой круговой. Высота ОО1= 12, а диаметр основания
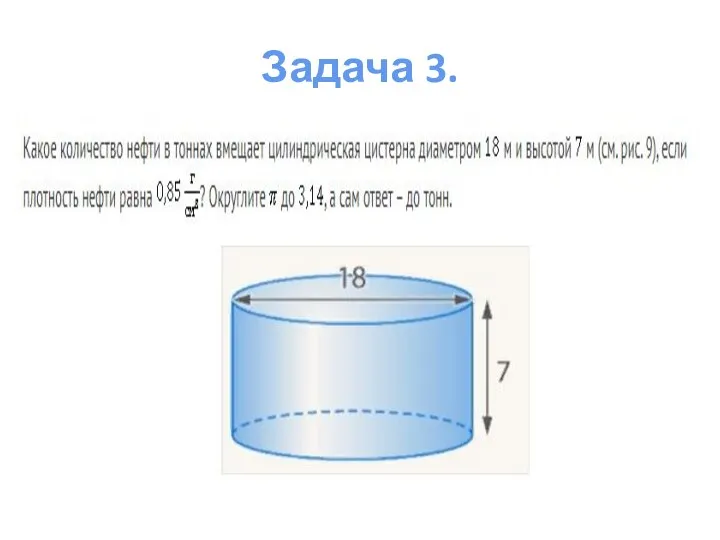
- 15. Задача 3.
- 16. Решение:
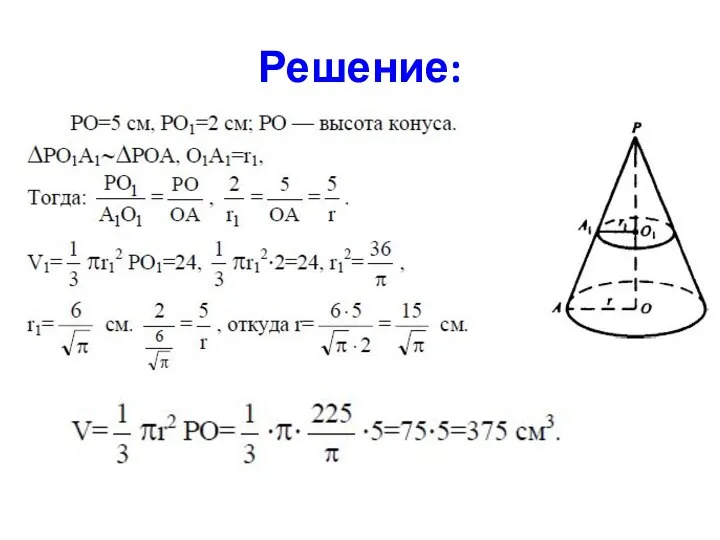
- 17. Задача 4.
- 18. Решение:
- 19. Решение:
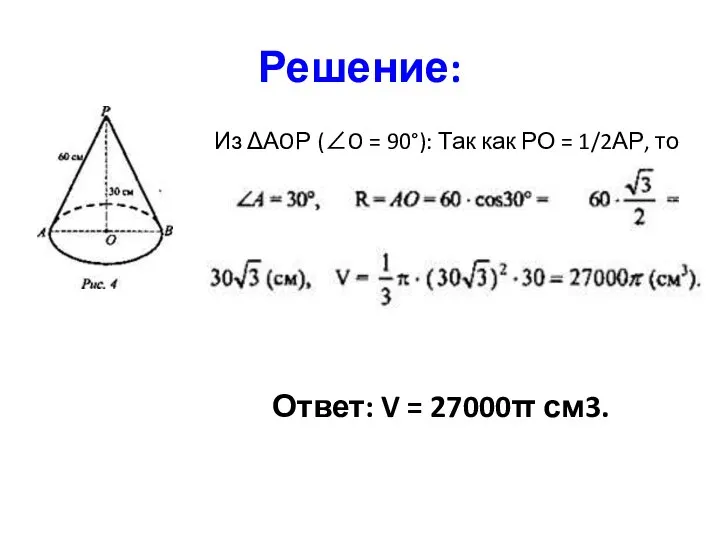
- 20. Образующая конуса равна 60 см, высота 30 см. Найдите Vконуса. Задача 5.
- 21. Решение: Из ΔАOР (∠O = 90°): Так как РО = 1/2АР, то Ответ: V = 27000π
- 22. Образующая конуса, равна 12 см, наклонена к плоскости основания под углом 30°. Найдите объем конуса. Задача
- 23. Решение: Из ΔАSO (∠O = 90°): Ответ: V= 216π см3
- 24. Образующая конуса наклонена к плоскости основания под углом 30 градусов, радиус основания равен 3 дм. Найти
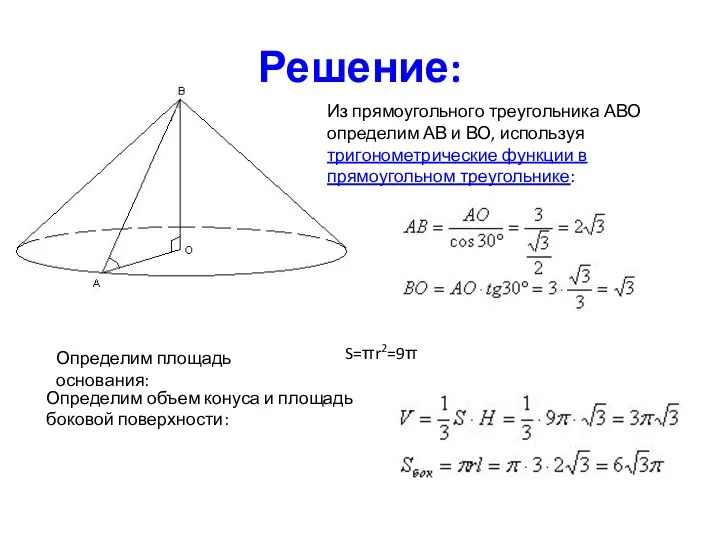
- 25. Решение: Из прямоугольного треугольника АВО определим АВ и ВО, используя тригонометрические функции в прямоугольном треугольнике: Определим
- 26. Высота усеченного конуса равна 2 корня из 3 см. Диагональ осевого сечения конуса образует с плоскостью
- 27. Решение: Рассмотрим треугольник ACD: в нем один из острых углов равен 30 градусов, т.е. катет противолежащий
- 28. Задача 9. (№702)
- 29. Решение:
- 30. Задача 10. (№708)
- 31. Решение: Дано: усеченный конус, r = О1С = 3 м, ОВ = R = 6 м,
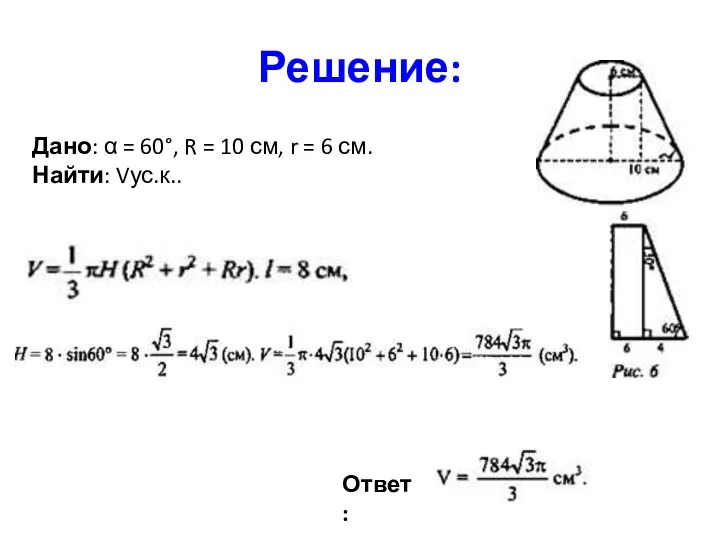
- 32. Задача 11. Радиус оснований усеченного конуса 6 см и 10 см. Образующая наклонена к плоскости большего
- 33. Решение: Дано: α = 60°, R = 10 см, r = 6 см. Найти: Vус.к.. Ответ:
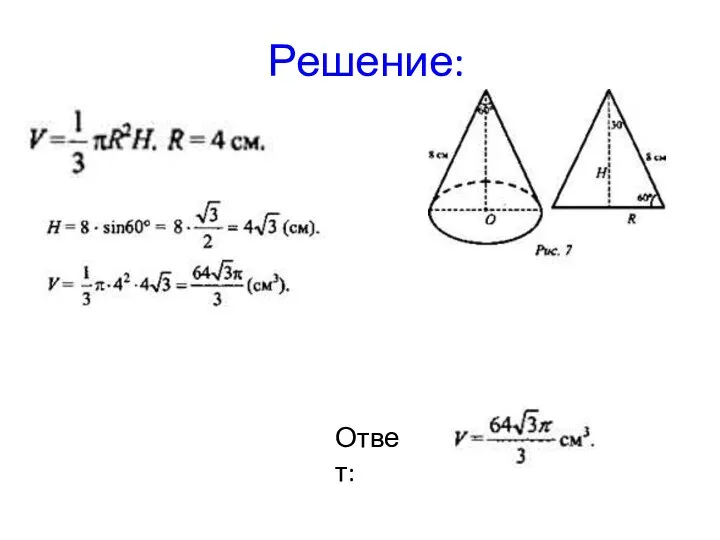
- 34. Образующая конуса 8 см, а угол при вершине осевого сечения 60°. Найдите объем конуса. Задача 12.
- 35. Решение: Ответ:
- 36. Найдите объем усеченного конуса, если его осевое сечение трапеция с основаниями 8 см, 6 см и
- 37. Решение: Ответ: V = 37π см3.
- 38. ДОМАШНЕЕ ЗАДАНИЕ: Написать опорный конспект. Выучить все формулировки теорем и формулы! Разобрать решенные задачи Подготовиться у
- 40. Скачать презентацию


























 Задача по математике (1 класс, задание 13.2)
Задача по математике (1 класс, задание 13.2) Как лгать при помоощи статистики
Как лгать при помоощи статистики Площадь прямоугольника
Площадь прямоугольника Случаи сложения 470 +80 и вычитания 560-90
Случаи сложения 470 +80 и вычитания 560-90 Устный счет. Действия с числами
Устный счет. Действия с числами Задачи математической статистики
Задачи математической статистики Теорема Пифагора. Учебник
Теорема Пифагора. Учебник Умножение числа 2 и наа 2
Умножение числа 2 и наа 2 Прибавления числа 2
Прибавления числа 2 Презентация на тему Объем цилиндра
Презентация на тему Объем цилиндра  Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Системы принятия решений. Определения
Системы принятия решений. Определения Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Великие математики древности. Архимед, Пифагор, Евклид, Фалес
Великие математики древности. Архимед, Пифагор, Евклид, Фалес Геометрическая прогрессия
Геометрическая прогрессия 20140130_dekada
20140130_dekada Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс МиРИ Введение. Разд 1. Осн Метр ВЛ
МиРИ Введение. Разд 1. Осн Метр ВЛ Математика. Ход игры
Математика. Ход игры Тригонометрические уравнения, приводимые к квадратным
Тригонометрические уравнения, приводимые к квадратным Решение задач с помощью пропорций
Решение задач с помощью пропорций Аксонометрические проекции. Самостоятельная работа
Аксонометрические проекции. Самостоятельная работа Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8
Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8 Треугольник
Треугольник Квадратные неравенства (8 класс)
Квадратные неравенства (8 класс) Способы решения уравнений с модулями
Способы решения уравнений с модулями Векторы в пространстве
Векторы в пространстве Признаки равенства треугольников
Признаки равенства треугольников