Угол между прямыми

УСЛОВИЕ ЗАДАЧИ
Дан четырехугольный параллелепипед ABCDA1B1C1D1. Найти угол между C1D и BF, где F- середина CD; если AD= ; CD=АА1= √2.

УГОЛ МЕЖДУ ПРЯМЫМИ:
- Углом между двумя пересекающимися
прямыми называется наименьший из углов,
образованных при пересечении прямых.
-Углом между скрещивающимися прямыми называется
угол между пересекающимися прямыми,
соответственно параллельными данным
скрещивающимся.
-Две прямые называются перпендикулярными,
если угол между ними равен 90.
-Угол между параллельными прямыми
считается равным нулю.

Задачу можно решить тремя способами:
1.Поэтапно-вычислительным методом
2.Координатным методом
3.Методом трех косинусов

ПОЭТАПНО-ВЫЧИСЛИТЕЛЬНЫЙ МЕТОД
При нахождении этим методом угла между прямыми m и l используют формулу:
где a и b  длины сторон треугольника АВС, соответственно параллельных этим
прямым.
Далее:

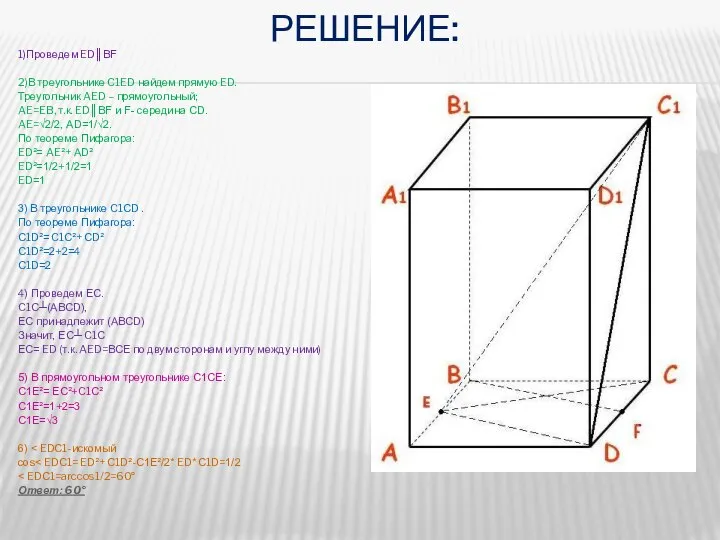
РЕШЕНИЕ:
1)Проведем ED║BF
2)В треугольнике C1ED найдем прямую ED.
Треугольник AED – прямоугольный;
AE=EB, т.к. ED║BF и F- середина CD.
AE=√2/2, АD=1/√2.
По теореме Пифагора:
ED²= AE²+ АD²
ED²=1/2+1/2=1
ED=1
3) В треугольнике C1СD .
По теореме Пифагора:
С1D²= C1С²+ СD²
С1D²=2+2=4
С1D=2
4) Проведем EC.
C1С┴(ABCD),
EC принадлежит (ABCD)
Значит, EC┴ C1С
EC= ED (т.к. AED=ВСЕ по двум сторонам и углу между ними)
5) В прямоугольном треугольнике С1СЕ:
С1Е²= EC²+C1С²
С1Е²=1+2=3
С1Е=√3
6) < EDС1-искомый
cos< EDС1= ED²+ С1D²-С1Е²/2* ED* С1D=1/2
< EDС1=arccos1/2=60°
Ответ: 60°

КООРДИНАТНЫЙ МЕТОД:
При нахождении угла между прямыми m и l используют формулу
где p и q - векторы, соответственно параллельные
этим прямым; в частности, для того чтобы прямые m
и l были перпендикулярны, необходимо и
достаточно чтобы p*q= 0.
Далее:

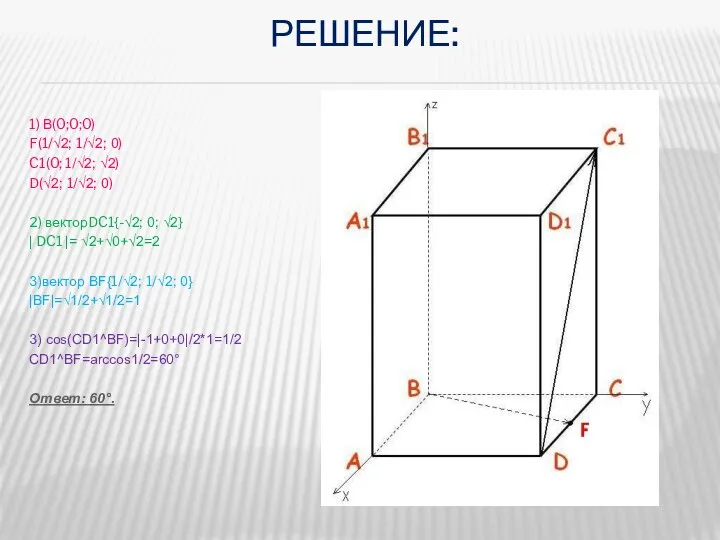
РЕШЕНИЕ:
1) В(0;0;0)
F(1/√2; 1/√2; 0)
C1(0; 1/√2; √2)
D(√2; 1/√2; 0)
2) векторDC1{-√2; 0; √2}
| DC1 |= √2+√0+√2=2
3)вектор BF{1/√2; 1/√2; 0}
|BF|=√1/2+√1/2=1
3) cos(CD1^BF)=|-1+0+0|/2*1=1/2
CD1^BF=arccos1/2=60°
Ответ: 60°.

МЕТОД ТРЁХ КОСИНУСОВ:
Соотношение cosγ=cosα*cosβ называют теоремой Пифагора для трёхгранного угла или теоремой о трёх косинусах.
Чтобы найти cos угла между скрещивающимися прямыми , нужно перемножить косинусы углов между данными прямыми и проекцией их на плоскость основания.
Далее:

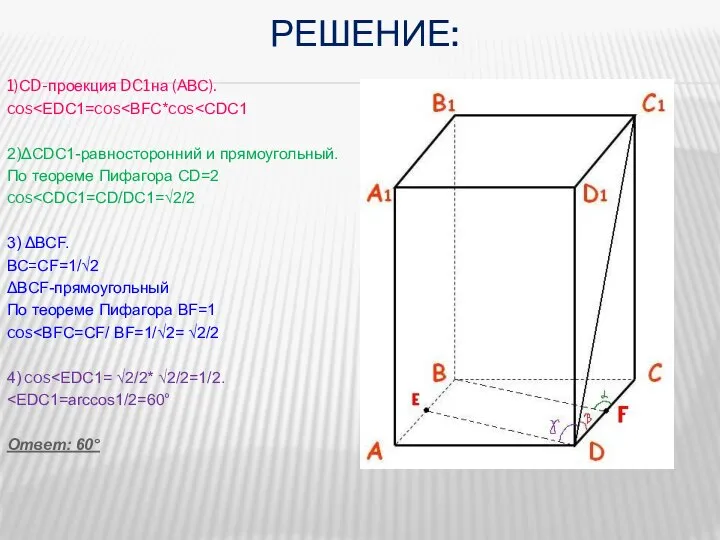
РЕШЕНИЕ:
1)СD-проекция DC1на (АВС).
cos
2)ΔCDC1-равносторонний и прямоугольный.
По теореме Пифагора CD=2
cos
3) ΔВСF.
ВС=СF=1/√2
ΔВСF-прямоугольный
По теореме Пифагора BF=1
cos BF=1/√2= √2/2
4) cos
Ответ: 60°