Содержание
- 2. Геометрия Планиметрия Стереометрия stereos - объемный, пространственный metreo - измеряю
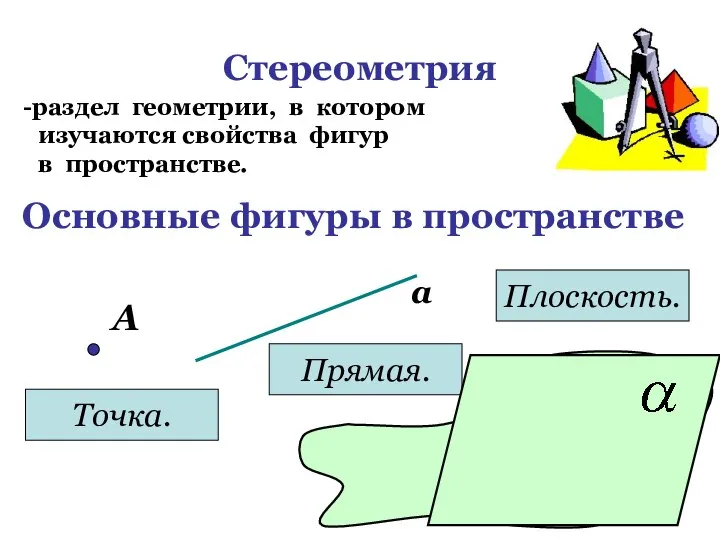
- 3. Стереометрия раздел геометрии, в котором изучаются свойства фигур в пространстве. Основные фигуры в пространстве А Точка.
- 4. СТЕРЕОМЕТРИЯ точка прямая плоскость A, B, C, … a, b, c, … или AВ, BС, CD,
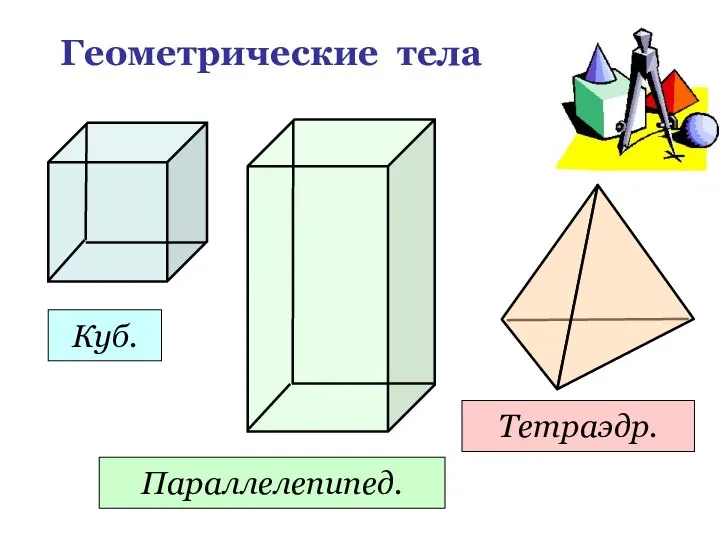
- 5. Геометрические тела Куб. Параллелепипед. Тетраэдр.
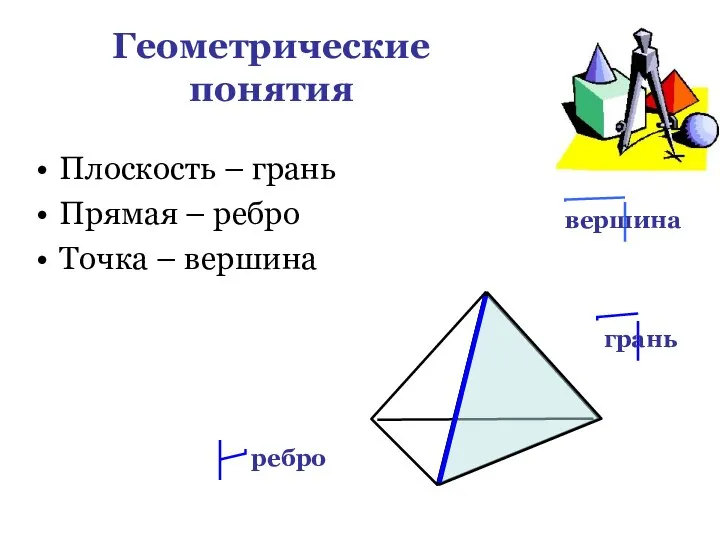
- 6. Геометрические понятия Плоскость – грань Прямая – ребро Точка – вершина вершина грань ребро
- 7. Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства
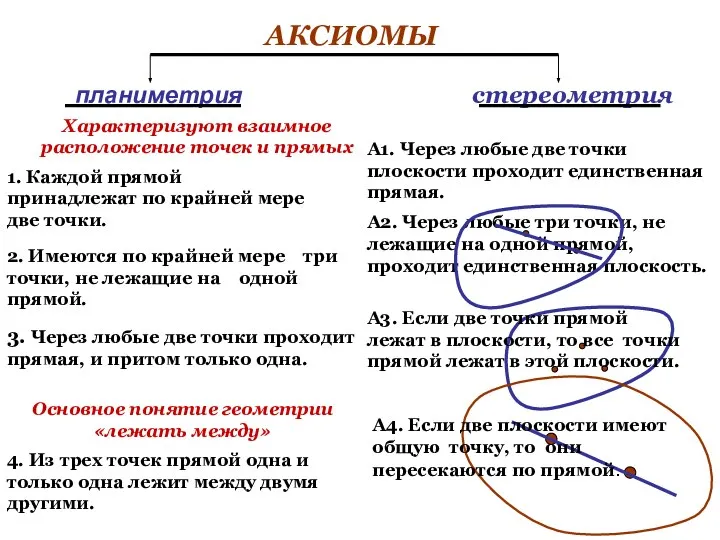
- 8. АКСИОМЫ планиметрия стереометрия 1. Каждой прямой принадлежат по крайней мере две точки. 2. Имеются по крайней
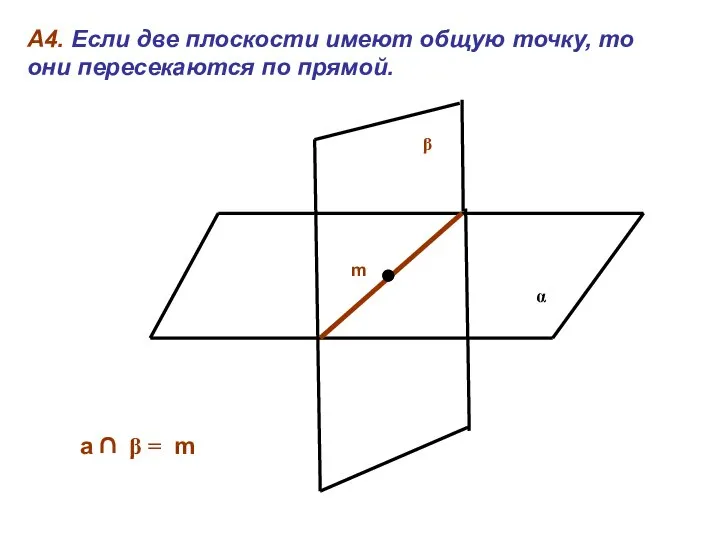
- 9. А4. Если две плоскости имеют общую точку, то они пересекаются по прямой. α β а ∩
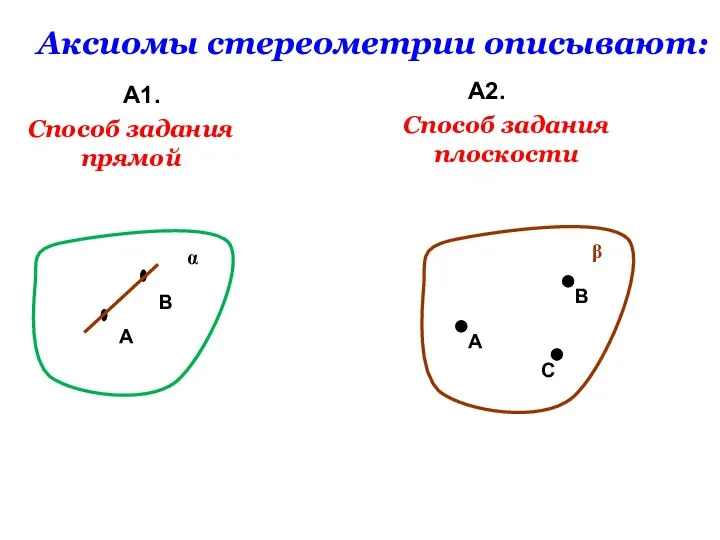
- 10. Аксиомы стереометрии описывают: А1. А2. А В С β Способ задания прямой α Способ задания плоскости
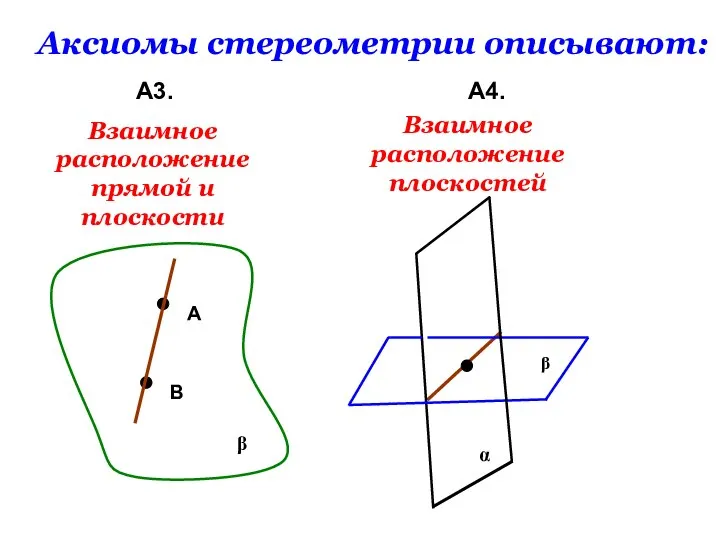
- 11. Аксиомы стереометрии описывают: А3. А4. β А В Взаимное расположение прямой и плоскости Взаимное расположение плоскостей
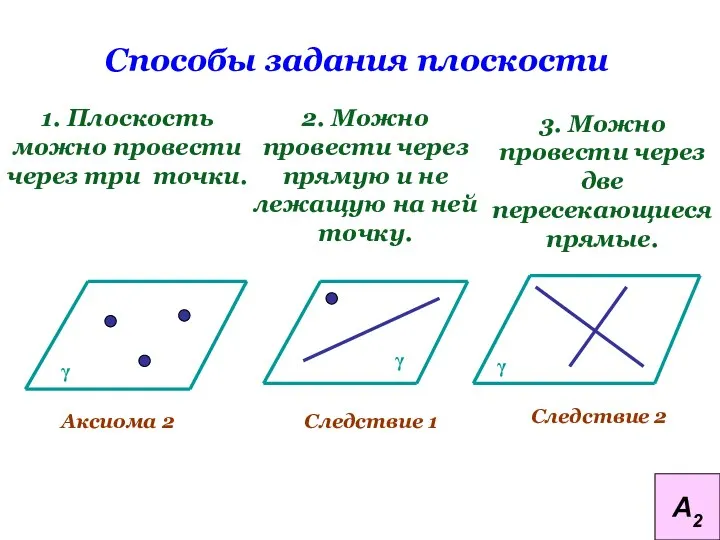
- 12. Способы задания плоскости 1. Плоскость можно провести через три точки. 2. Можно провести через прямую и
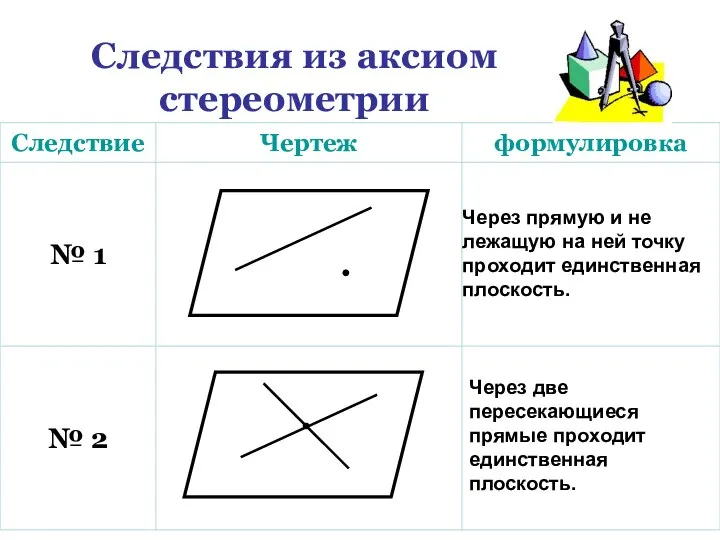
- 13. Следствия из аксиом стереометрии Через прямую и не лежащую на ней точку проходит единственная плоскость. Через
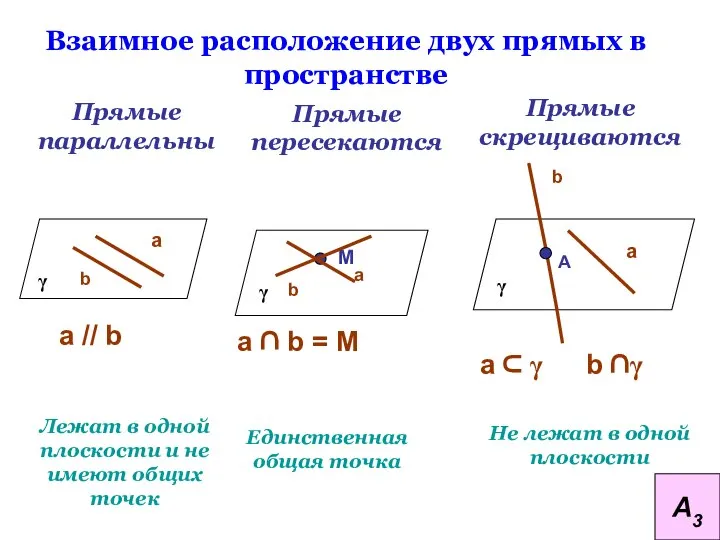
- 14. Взаимное расположение двух прямых в пространстве Прямые параллельны Прямые пересекаются Прямые скрещиваются Единственная общая точка Не
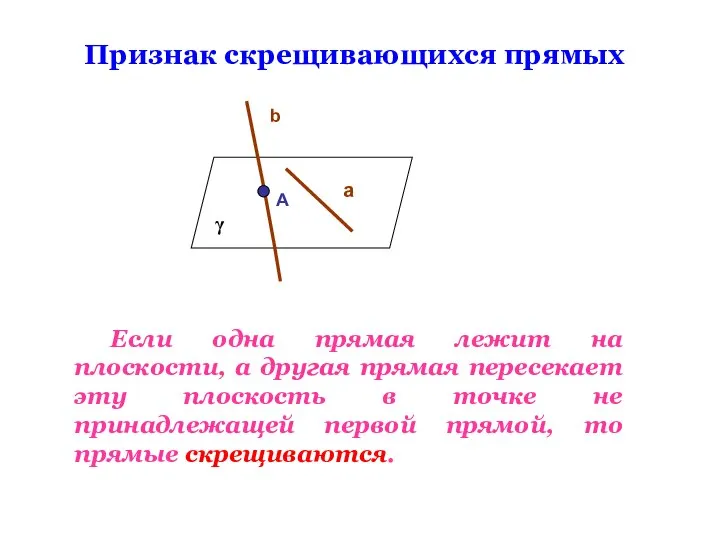
- 15. Признак скрещивающихся прямых Если одна прямая лежит на плоскости, а другая прямая пересекает эту плоскость в
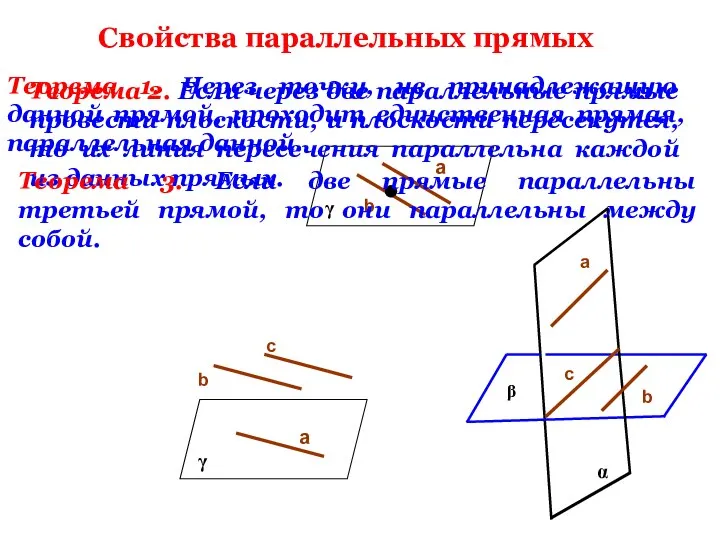
- 16. Свойства параллельных прямых b Теорема 1. Через точку, не принадлежащую данной прямой, проходит единственная прямая, параллельная
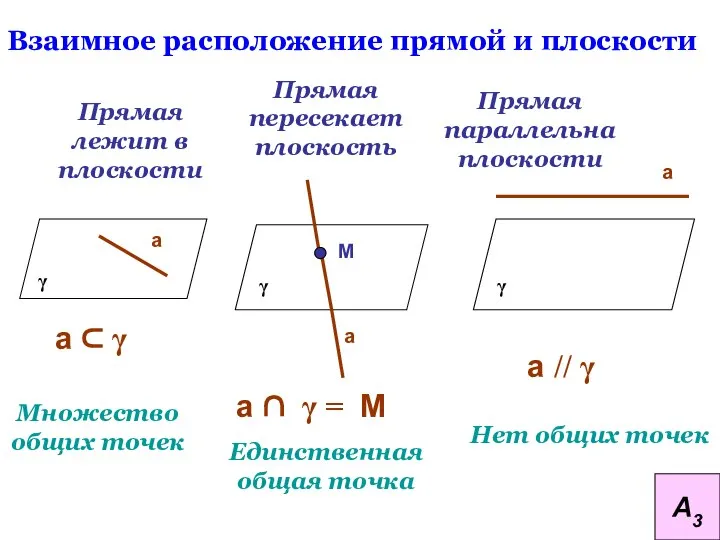
- 17. Взаимное расположение прямой и плоскости Прямая лежит в плоскости Прямая пересекает плоскость Прямая параллельна плоскости Множество
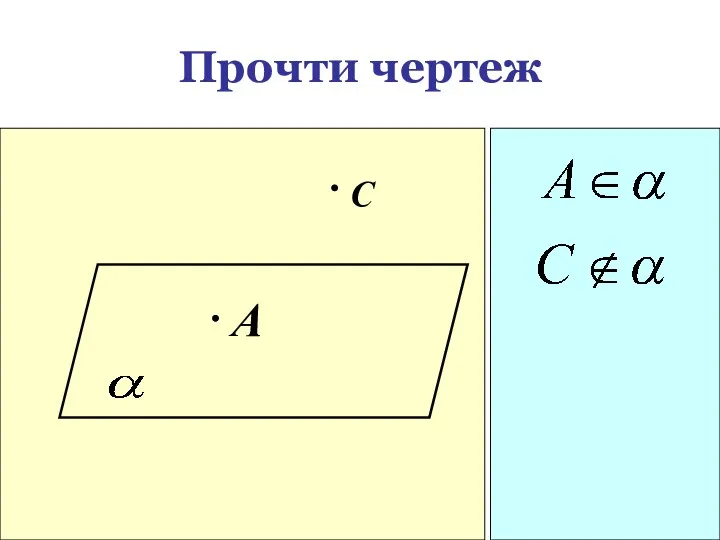
- 18. Прочти чертеж A С
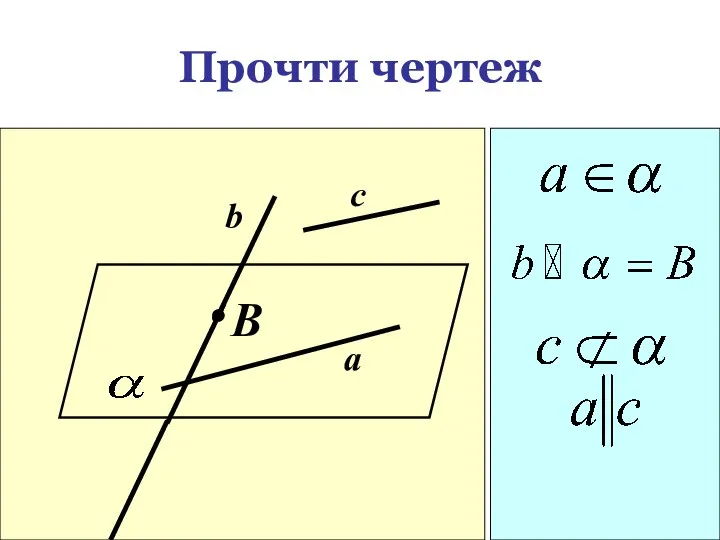
- 19. Прочти чертеж B c b a
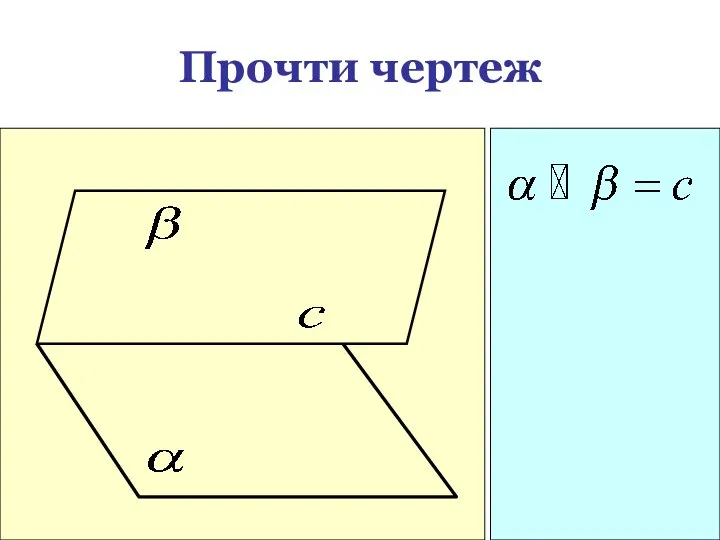
- 20. Прочти чертеж
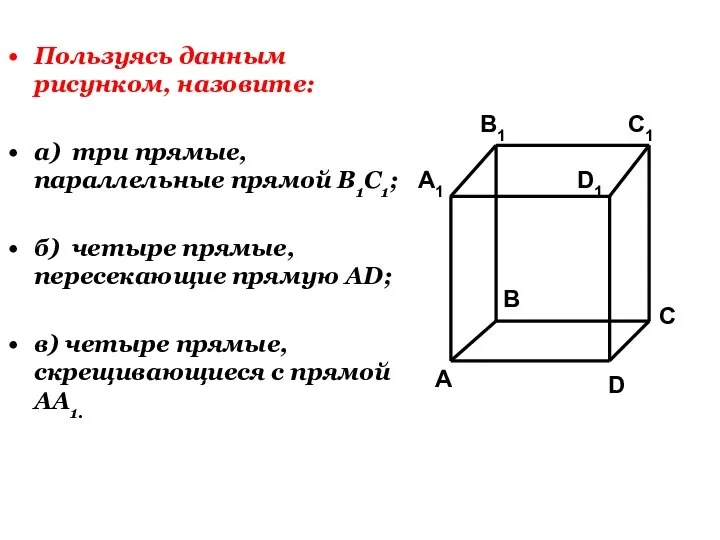
- 21. Пользуясь данным рисунком, назовите: а) три прямые, параллельные прямой В1С1; б) четыре прямые, пересекающие прямую AD;
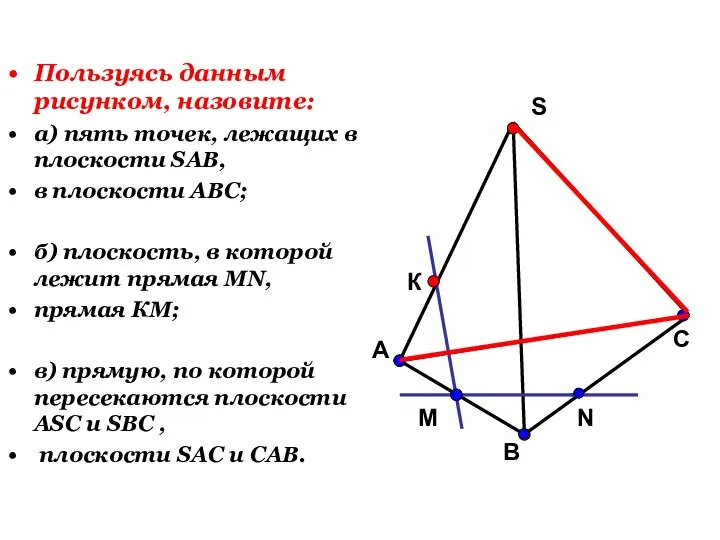
- 22. Пользуясь данным рисунком, назовите: а) пять точек, лежащих в плоскости SAB, в плоскости АВС; б) плоскость,
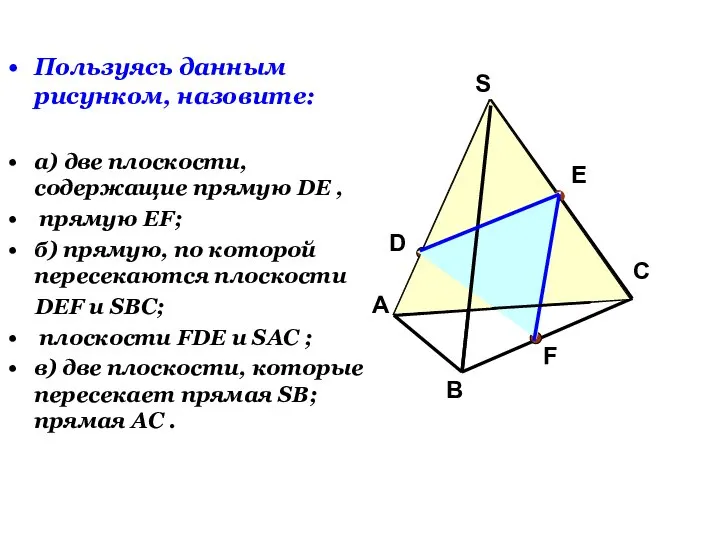
- 23. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE , прямую EF; б) прямую, по
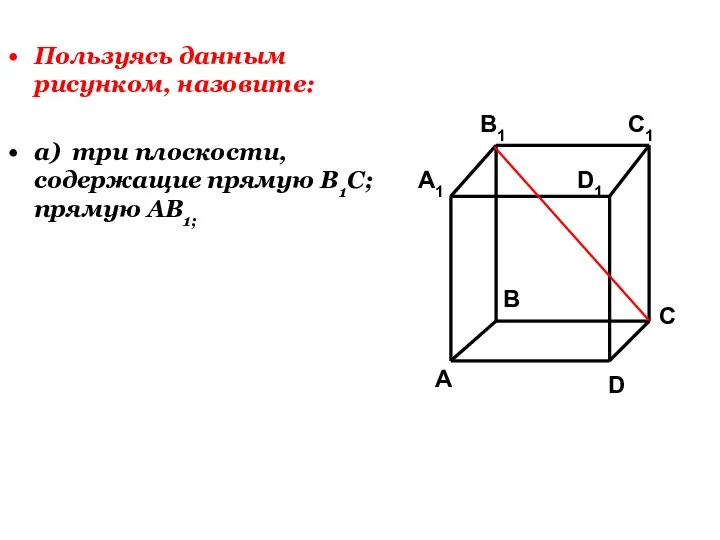
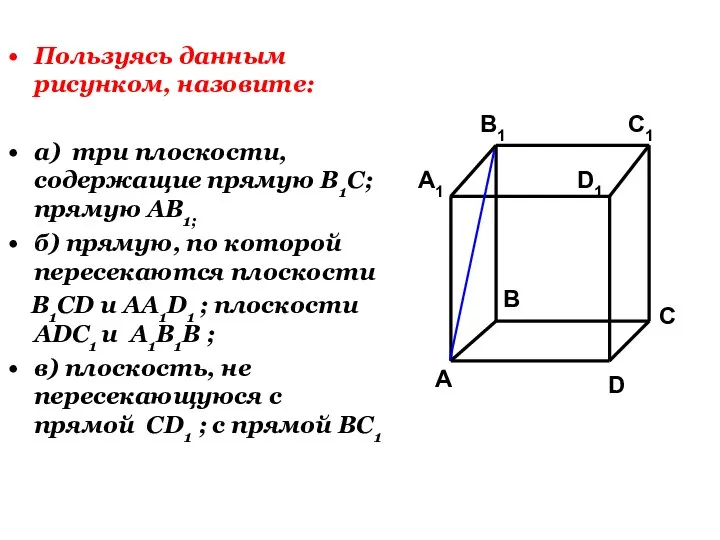
- 24. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1;
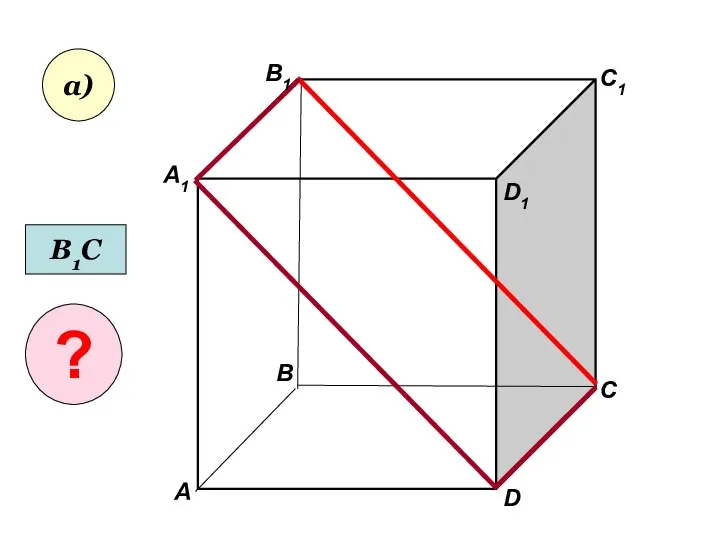
- 25. А А1 В В1 С D1 D C1 а) В1С ?
- 26. А А1 В В1 С D1 D C1 а) В1С ?
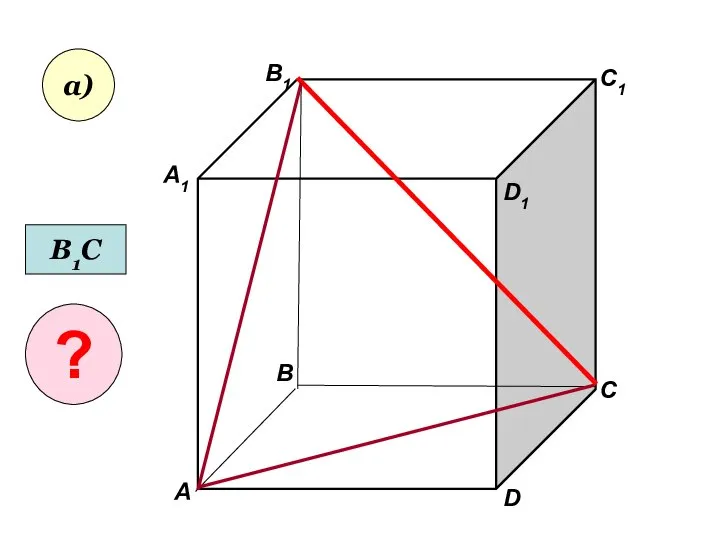
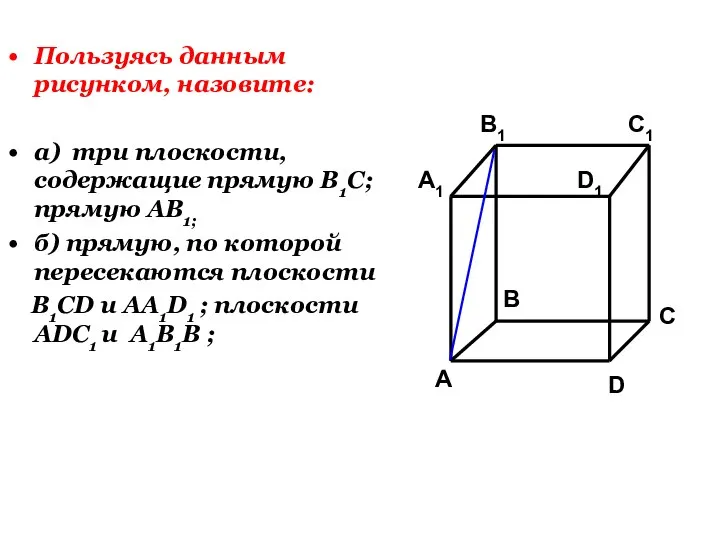
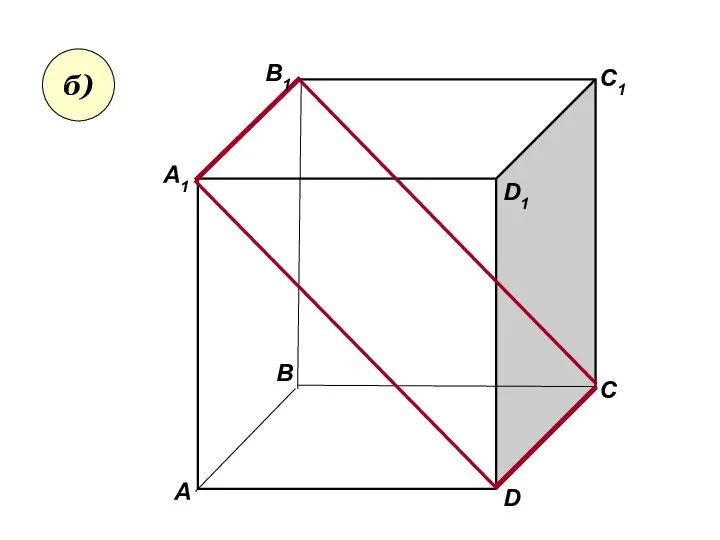
- 27. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 28. А А1 В В1 С D1 D C1 б)
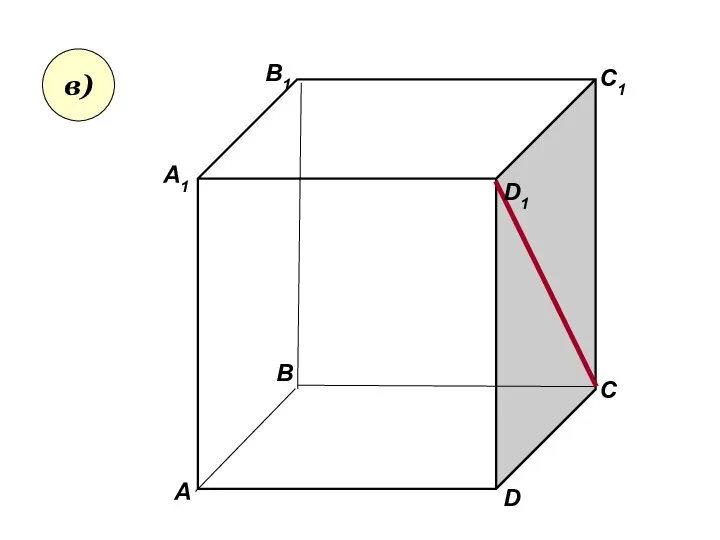
- 29. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 30. А А1 В В1 С D1 D C1 в)
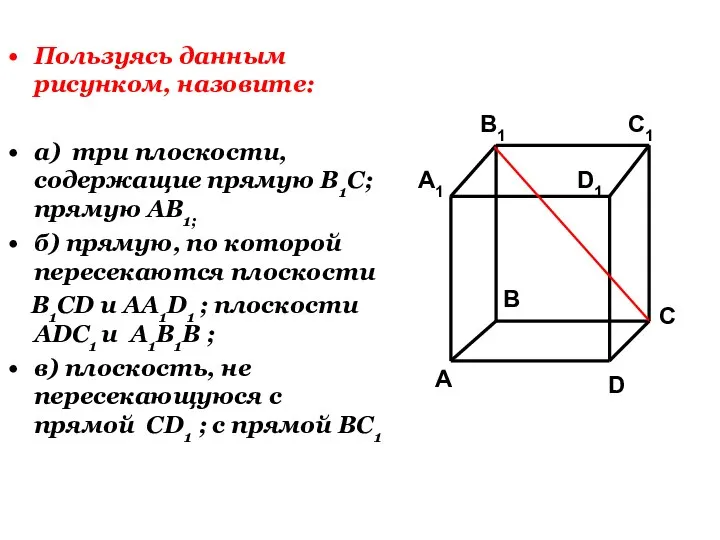
- 31. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 32. Ответьте на вопросы: Верно ли, что две прямые параллельны, если они не имеют общих точек? Верно
- 34. Скачать презентацию



 Признаки равенства треугольников
Признаки равенства треугольников методы решения тригонометрических уравнений
методы решения тригонометрических уравнений Приключения Буратино в Стране Финансов
Приключения Буратино в Стране Финансов Свойства медианы равнобедренного треугольника
Свойства медианы равнобедренного треугольника Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Комплексные числа
Комплексные числа Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Урок–путешествие в страну Дроби
Урок–путешествие в страну Дроби Тригонометрические уравнения. Уравнение cos x=a
Тригонометрические уравнения. Уравнение cos x=a Определение двойного интеграла
Определение двойного интеграла Презентация на тему Раскрытие скобок (5 класс)
Презентация на тему Раскрытие скобок (5 класс)  Призма. Решение задач
Призма. Решение задач Могла ли математика спасти Пахома, или Площадь
Могла ли математика спасти Пахома, или Площадь Равнобедренный треугольник
Равнобедренный треугольник Свойства тригонометрических функций
Свойства тригонометрических функций Треугольники. ЕГЭ
Треугольники. ЕГЭ Пирамида
Пирамида Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Скалярное произведение векторов
Скалярное произведение векторов Трапеция. Площадь криволинейной трапеции
Трапеция. Площадь криволинейной трапеции Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)
Презентация на тему Цилиндры и цилиндрические поверхности (11 класс)  Меньше или больше ГБОУ ЦО № 354 учитель математики Иванова И.В.
Меньше или больше ГБОУ ЦО № 354 учитель математики Иванова И.В.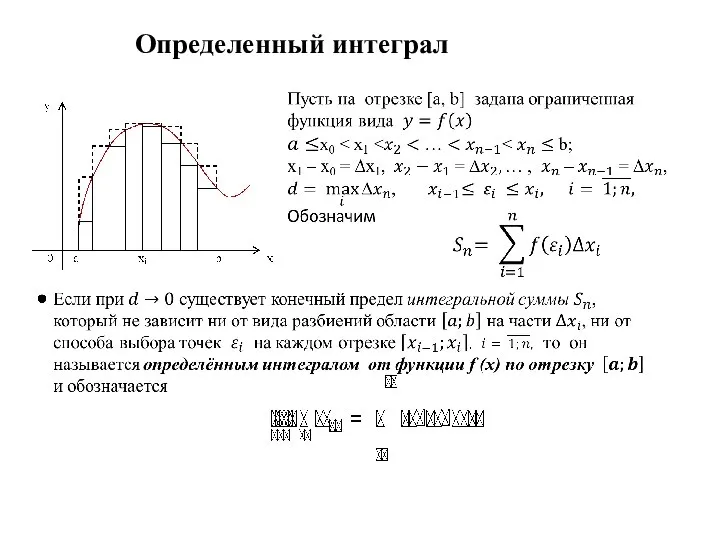 Определённый интеграл
Определённый интеграл Прямая, луч, отрезок
Прямая, луч, отрезок Сложение и вычитание векторов
Сложение и вычитание векторов Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ»
Доли и дроби. 5 класс Новоселова Е.А. МКОУ «Усть-Мосихинская СОШ» Презентация на тему Математика - царица наук
Презентация на тему Математика - царица наук  Градусное измерение углов. Сумма углов в треугольнике. Тест
Градусное измерение углов. Сумма углов в треугольнике. Тест