Содержание
- 2. Зміст лекції. 1. Поняття предикату. 2. Квантори. 3. Формули логіки предикатів. 4. Интерпретація. Модель. 5. Правила
- 3. Поняття «предикат» узагальнює поняття «висловлювання». Неформально кажучи, предикат - це висловлювання, в яке можна підставляти аргументи.
- 4. Предикат – розповідне речення, що містить предметні змінні, визначені на відповідних множинах. При заміні змінних конкретними
- 5. Визначення і приклади. Предикатом називається розповідне речення про елементи деякої заданої множини M, яке (речення) стає
- 6. Існують такі види логічних міркувань, які не можуть бути обґрунтовані в рамках обчислення висловлювань. Ось приклади
- 7. Квантори Квантор - логічна операція, яка дає кількісну характеристику предметної області, до якої відноситься вираз, одержуване
- 8. Квантором загальності називають символ ∀, під дією якого предикат P (x), визначений на множині М, приймає
- 9. Приклад 1. Задано предикат: «х любить у» - позначимо його Р (х, у). ∀х∃уР(х,у) – всяка
- 10. Логіка предикатів На сукупності всіх предикатів, заданих на множині М, додаються знайомі по логіці висловлень операції
- 11. На предикати можна дивитися і більш формально, причому з двох точок зору. По-перше, предикат можна представити
- 12. Означення. Множиною (областю) істинності предиката Р(x1,…,xn) , заданого на множині М ⊂ (М1×М2×…Мn), називається сукупність всіх
- 13. Теорема. Предикат Р(x1,…,xn), заданий на множині М ⊂ (М1×М2×…Мn), буде: 1) тотожно істинним ⇔ Мр =
- 14. Визначення. Інтерпретацією на непорожній множині М називається функція, задана на сигнатурі F∪R, що 1) константі ставить
- 15. Приклад. Нехай сигнатура складається із символу одномісного предиката P і двомісного предиката D, M={2,3,6,9,12,15} і
- 16. Одним з основних типів задач цієї теми є задачі, пов'язані з використанням виразних можливостей мови логіки
- 17. Тоді міркування запишемо у вигляді наступної послідовності формул. Н1=(∀ x)[Д(х)→ (∃y)(C(y)^З(x,y))], H2=(∀ x)(∀ y)[Д(x) ^ПЛ(y )
- 18. Визначення Формули F(x1,…,xn) і G(x1,…,xn) називаються рівносильними, якщо для будь-якої інтерпретації з областю М висловлення F(a1,…,an)
- 19. Логіка першого порядку (числення предикатів) Логіка першого порядку (числення предикатів) - формальне числення, яка допускає висловлювання
- 20. Більш складні конструкції визначаються індуктивно: Терм є символ змінної або предметної константи, або має вигляд fin
- 21. Аксіоматика і доведення формул Система логічних аксіом логіки першого порядку складається з аксіом числення висловів доповненої
- 22. Використання Будучи формалізованим аналогом звичайної логіки, логіка першого порядку дає можливість строго міркувати про істинність і
- 23. Рівносильні формули логіки предикатів. Визначення 1. Дві формули логіки предикатів А і В називаються рівносильними на
- 24. Ясно, що всі рівносильности алгебри висловлювань будуть вірними, якщо в них замість змінних висловлювань підставити формули
- 25. Рівносильність 1 означає той простий факт, що, якщо не для всіх х істинно А (х), то
- 26. У логіці предикатів, як і в логіці висловлень, формули можуть мати нормальну форму, тобто існують еквіваленті
- 28. Скачать презентацию















![Тоді міркування запишемо у вигляді наступної послідовності формул. Н1=(∀ x)[Д(х)→ (∃y)(C(y)^З(x,y))], H2=(∀](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1183541/slide-16.jpg)









 Решите неравенства
Решите неравенства Числовые и буквенные выражения
Числовые и буквенные выражения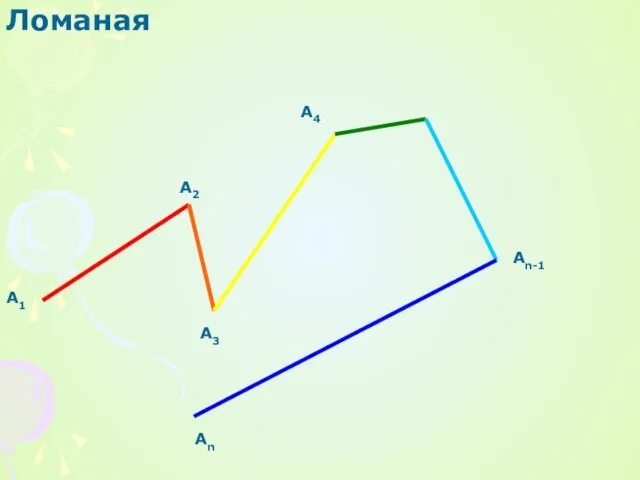 Презентация на тему Ломаная
Презентация на тему Ломаная  Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Математическая статистика
Математическая статистика Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Построение сечений
Построение сечений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА
Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА  Серединный перпендикуляр
Серединный перпендикуляр Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Сложение чисел
Сложение чисел Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Площадь трапеции
Площадь трапеции Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Величины. Свойства величин
Величины. Свойства величин Функции. ЕГЭ
Функции. ЕГЭ Многочлены. Задания
Многочлены. Задания Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Умножение. Законы умножения
Умножение. Законы умножения Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Пушкин и математика
Пушкин и математика