15 задание. Виды. Делимость. Числовая последовательность. Конъюнкция. Множества

Делимость
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
(¬ДЕЛ(x, А) ∧ ДЕЛ(x, 21)) → ¬ДЕЛ(x, 14)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
План решения
1. Убрать следствия
2. Построить числовую прямую
3. Инвертировать часть без А (чтобы выражение зависело от А)
5. Найти промежуток, где должна быть А
4. Найти на прямой решение инверсии

Делимость на компе
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула
ДЕЛ(120, A) ∧ (¬ДЕЛ(x, A) → (ДЕЛ(x, 36) → ¬ДЕЛ(x, 15)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Решаем на компе!
Проходимся циклом по значениям “а” и “x”, подставляя их под условия.
False, потому что нам нужно, чтобы утверждение выполнялось при всех
значениях x. Поэтому выводим только когда утверждение не было ложно.

Числовая последовательность

Числовая последовательность на компе
Для какого наибольшего целого неотрицательного числа А выражение
(x2 – 11x + 28 > 0) ∨ (y2 – 9y + 14 > 0) ∨ (x2 + y2 > A)
тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y?
Проходимся циклом по значениям “а”, “у” и “x”, подставляя их под условия.
False, потому что нам нужно, чтобы утверждение выполнялось при всех
значениях x и y. Поэтому выводим только когда утверждение не было ложно.

Конъюнкция
Конъюнкция тоже самое, что и умножение, но в 2-ой системе счисления. То есть переводим все числа в 2-ую систему. И смотрим, где при умножении у на должно быть 0. Подставляем под все 1 нули. То есть получается число _ 0 _ _ 0 _ _. Далее подставляем это число под 102. Получаем:
1100110
_0__0__
При умножении не должно быть 0, получается это будет при значении:
1000000, либо при значении 0000010. Совмещаем эти случаи и получаем число 1000010. Переводим число в 10-ую с.с. и получаем 66

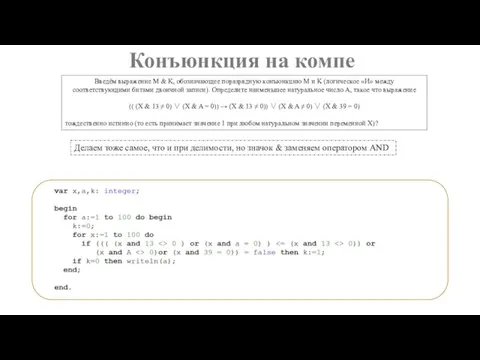
Конъюнкция на компе
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи). Определите наименьшее натуральное число A, такое что выражение
(( (X & 13 ≠ 0) ∨ (X & A = 0)) → (X & 13 ≠ 0)) ∨ (X & A ≠ 0) ∨ (X & 39 = 0)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной X)?
Делаем тоже самое, что и при делимости, но значок & заменяем оператором AND