Слайд 2ЦЕЛЬ УРОКА:
совершенствовать знания, умения и навыки решения линейных уравнений

Слайд 3
Эпиграф к уроку:
Пусть математика сложна,
Ее до края не познать,
Откроет

двери всем она,
В них только надо постучать
Слайд 9Уравнение - равенство с одной
и более неизвестными переменными
Что называется уравнением?

Слайд 10Какие виды уравнений вам известны?
Линейные уравнения с одной переменной

Слайд 11Какие из данных уравнений являются линейными?
1) x(х+7)=0 5) 9x = 1
2)

х3 – 5х + 6 = 0 6) 9х2 = 18
3) │x│=11 7) 7(x-2) = 7x-14
4) 3x - 1 =14 8) │x4 - 3│=1
Слайд 13
Что называется линейным уравнением с одной переменной?
Уравнение вида: ах + b =

0 называется линейным уравнением с одной переменной, где х- переменная; а и b – некоторые числа.
ВНИМАНИЕ!
Переменная х входит в уравнение обязательно в первой степени
Слайд 14Что значит - решить линейное уравнение с одной переменной?
Решить линейное уравнение с

одной переменной – это значит найти все корни уравнения или доказать, что их нет
Слайд 15
Что называется корнем уравнения?
Корень уравнения – значение переменной, при котором уравнение обращается

в верное числовое равенство
Слайд 16
Не решая уравнения, проверьте какое из чисел является его корнем
43; 13;

32; 0
67+(33-х)=68
Слайд 17Если х = 43, то 67 + (33-43) = 68;
57=68 –

НЕВЕРНО
Если х = 13, то 67 + (33-13) = 68;
87 = 68 - НЕВЕРНО
Если х = 32, то 67 + (33-32) = 68;
68 = 68 - ВЕРНО
Если х= 0, то 67 + (33 – 0 ) = 68;
100 = 68 - НЕВЕРНО
Слайд 18Правила и определения, применяемые при решении линейных уравнений с одной переменной

Слайд 19Правило раскрытия скобок перед которыми стоит знак «+»
Если перед скобками стоит знак

«+», это значит, что все слагаемые в скобках надо умножить на 1, т. е., раскрывая скобки, оставить их без изменения
Слайд 20Правило раскрытия скобок перед которыми стоит знак «-»
Если перед скобками стоит знак

«–», это значит, что все слагаемые в скобках надо умножить на –1, т. е., раскрывая скобки, изменить знаки слагаемых на противоположные
Слайд 21Какие слагаемые называются подобными?
Подобные слагаемые – это слагаемые, имеющие одинаковую буквенную часть

или не имеющие ее вовсе
Слайд 22
Как привести подобные слагаемые?
Привести подобные слагаемые – это значит, сложить их коэффициенты

и результат умножить на общую буквенную часть
Слайд 23
Алгоритм решения линейных уравнений с одной переменной
1.Раскрыть скобки.
2.Собрать члены, содержащие неизвестные, в

одной части уравнения, а остальные члены в другой.
3.Привести подобные слагаемые в обеих частях уравнения.
4.Разделить обе части уравнения на коэффициент при неизвестном
Слайд 24
Cколько корней может иметь уравнение?

Слайд 25Как называются уравнения, которые имеют одинаковые корни?
Уравнения, которые имеют одинаковые корни, называются

равносильными
Слайд 26
Составьте пары равносильных уравнений
1) х+1 = 3 5) х-3=0
2) 2х - 7

=12 6) 5х = 0
3) (4+х) – 2 =2 7) х-3,5 = 2
4) -5х = - 6 8) 4х=8
Слайд 27
ОТВЕТ
1) х+1 = 3 5) х-3=0
2) 2х - 7 =12 6) 5х

= 0
3) (4+х) – 2 =2 7) х-3,5 = 2
4) -5х = - 6 8) 4х=8
Слайд 28
При решении уравнений используют свойства:
1. Если в уравнении перенести слагаемые из одной

части в другую, изменив его знак, то получится равносильное уравнение
2. Если обе части уравнения умножить или разделить на число (не равное нулю), то получится равносильное уравнение
Слайд 29Где используются линейные уравнения?
В решении задач

Слайд 30Какой метод в математике используется в решении задач?
Метод математического
моделирования

Слайд 31Что чаще всего выбирается за математическую модель ?
Линейное уравнение
с одной
переменной

Слайд 32ЗАДАНИЕ
Дано описание ситуации. Составьте
математическую модель данной ситуации.
На первой автостоянке стояло

в 8 раз
автомобилей больше, чем на второй. Когда с первой автостоянки на вторую перевезли 25 автомобилей, то на второй стоянке
оказалось в 2 раза больше машин, чем на
первой. Сколько автомобилей было на
каждой стоянке первоначально?
Слайд 33РЕШЕНИЕ
Пусть х автомобилей было на второй автостоянке
По условию задачи, составим уравнение:
х+25

= 2( 8х - 25)
Слайд 34ИТОГИ УРОКА
Вспомнили правила и алгоритм , используемые при решении уравнений;
Научились решать линейные

уравнения с одной переменной;
Убедились в значимости применения уравнений как математических моделей в решении задач;
Научились составлять линейные уравнения с одной переменной при заданных условиях задачи

































 Разряды чисел
Разряды чисел Луч и угол
Луч и угол Описание методов статистической обработки данных
Описание методов статистической обработки данных Своя игра. Сильное звено
Своя игра. Сильное звено Конус - тело вращения
Конус - тело вращения Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини
Лічба в межах 20. Складання і розв’язування задач на знаходження суми й остачі. Побудова відрізків заданої довжини Порядок выполнения действий в числовых выражениях
Порядок выполнения действий в числовых выражениях Площадь треугольника
Площадь треугольника Сравниваем выражения. 2 класс
Сравниваем выражения. 2 класс Математические ребусы. 2 класс
Математические ребусы. 2 класс Случаи вычитания 14 -
Случаи вычитания 14 -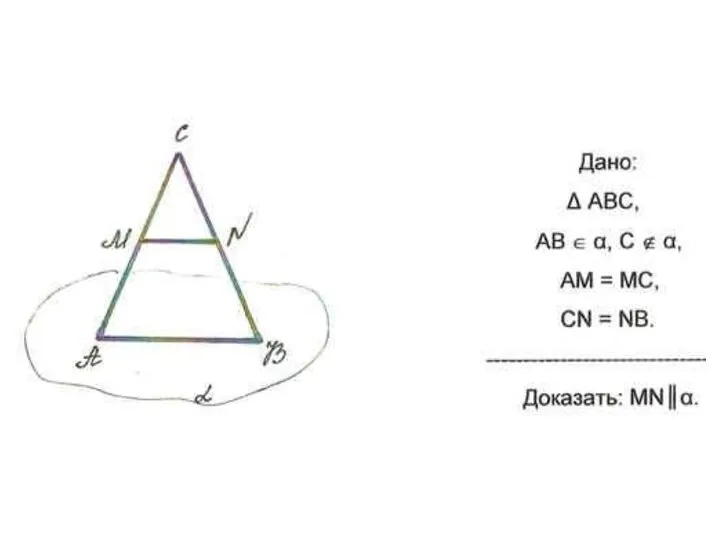 Параллельные прямые. Решение задач
Параллельные прямые. Решение задач Презентация на тему Задачи на проценты
Презентация на тему Задачи на проценты  Решение задач
Решение задач Умножение обыкновенных дробей
Умножение обыкновенных дробей Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Шкалы и координаты
Шкалы и координаты Асимптоты графика функции
Асимптоты графика функции Преобразование рациональных выражений
Преобразование рациональных выражений Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители В мире магических чисел
В мире магических чисел Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)
Презентация на тему Задачи на увеличение и уменьшение числа (1 класс)  Уравнение х2=a
Уравнение х2=a Прибавление и вычитание числа 3. 1 класс
Прибавление и вычитание числа 3. 1 класс