Компланарные вектора

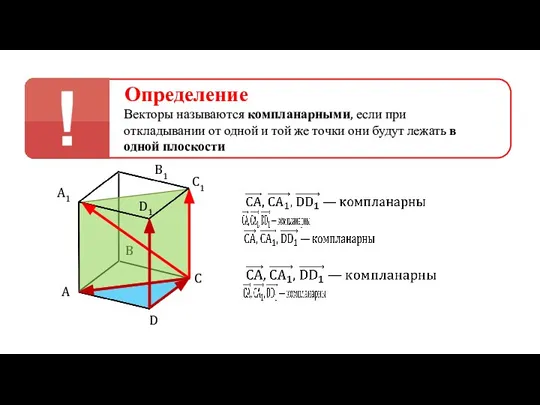
Определение
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости
C
A
B
D
A1
B1
C1
D1

— Любые два вектора компланарны
— Три вектора, среди которых имеются два коллинеарных, также компланарны
— Три произвольных вектора могут быть как компланарными, так и некомпланарными

Признак компланарности трёх векторов
Доказательство:
B1
C
A1
O
A
B
Что и требовалось доказать

Утверждение, обратное признаку компланарности векторов:

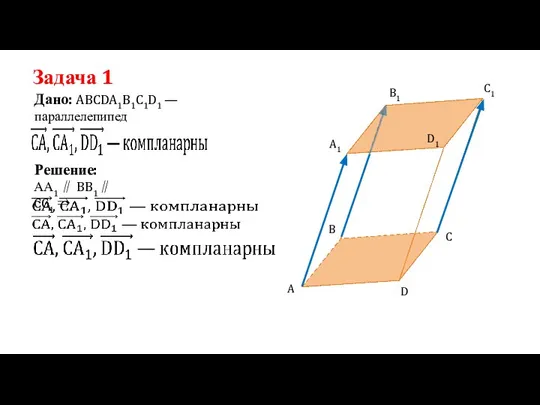
Задача 1
Дано: ABCDA1B1C1D1 —параллелепипед
Решение:
АА1 ∥ BB1∥ CC1 ⇒
A
D
C
B
B1
A1
D1
C1