Содержание
- 2. Самый отдаленный пункт земного шара к чему-нибудь да близок, а самый близкий от чего-нибудь да отдален
- 3. План лекции 1. Средняя, её сущность и определение 2. Виды и формы средних величин 3. Средняя
- 4. В средней величине взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и проявляются
- 5. Взаимодействие элементов совокупности приводит к ограничению вариации хотя бы части их свойств.
- 6. Главное значение средних величин состоит в их обобщающей функции, то есть замене индивиду-альных значений признака средней
- 7. Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной
- 8. Системные средние - характеристики государства как единой экономической системы
- 9. Метод средних не ограничивается только расчетом средней арифметической, существуют и другие виды средних.
- 10. Определить среднюю можно через исходное соотношение средней (ИСС) или ее логическую формулу: ИСС=(Суммарное значение или объем
- 11. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета
- 12. Для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
- 15. От того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет
- 16. средняя арифметическая; средняя гармоническая; средняя геометрическая; средняя квадратическая, кубическая и т.д.
- 17. Перечисленные средние объединяются в общей формуле степенной средней (при различной величине k)
- 20. Изменение показателя степени k приводит в каждом отдельном случае к определенному виду средней
- 29. Поскольку вариационные ряды обычно сгруппированы по одинаковым значениям признака, либо в интервалах его значений, то чаще
- 32. Во всех формулах xi –индивидуальные значения признака; fi – частота повторения индивидуального значения признака, n –
- 33. Чем больше показатель степени, тем больше величина соответствующей средней (мажорантность средних):
- 38. Сделки по акциям эмитента "Х" за торговую сессию
- 41. В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях
- 43. Часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса
- 44. Можно ли по имеющимся данным определить среднюю себестоимость данной продукции по двум предприятиям, вместе взятым? Можно,
- 45. Использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.
- 46. При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их
- 48. Для определения среднего возраста персонала найдем середины возрастных интервалов. При этом величины открытых интервалов (первого и
- 49. Средняя гармоническая Время на изготовление одной детали (x) в часах: 0,2; 0,3; 0,3; 0,5; 0,5 Требуется
- 51. Для решения необходимы данные об общих затратах времени всех пяти рабочих и о числе выработанных за
- 52. За это время первый рабочий выработает 1/0,2=5 деталей, второй и третий по 1/0,3=3,3 детали, а четвертый
- 53. В среднем на одну деталь затрачивалось 5/15,6=0,32 часа. Если все расчеты представить в виде формулы, то
- 56. В целом ряде случаев применение средней арифметической или средней гармонической определяется лишь наличием исходных данных.
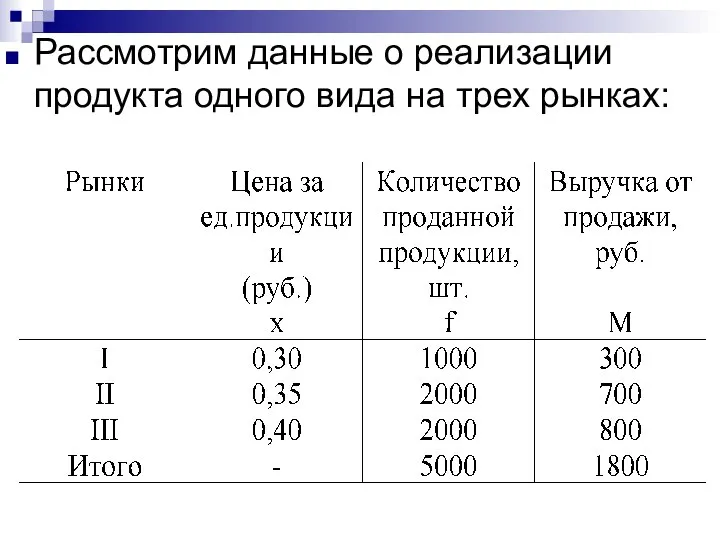
- 57. Рассмотрим данные о реализации продукта одного вида на трех рынках:
- 58. Требуется рассчитать среднюю цену, по которой продавался товар. 1) Предположим, мы располагаем только данными о ценах
- 61. Теперь предположим, что количество проданного товара неизвестно, а известны лишь цены и выручка от продажи.
- 68. В результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было
- 70. Средняя геометрическая Предположим, Вы внесли деньги в банк на срочный депозит, процент по которому ежегодно изменяется
- 72. P – первоначальная сумма вклада - доход по вкладу в первый, второй, третий и четвертый годы
- 79. Пример. В результате инфляции за первый год цена товара возросла в два раза к предыдущему году,
- 81. Скачать презентацию













































































 Решите неравенства
Решите неравенства Числовые и буквенные выражения
Числовые и буквенные выражения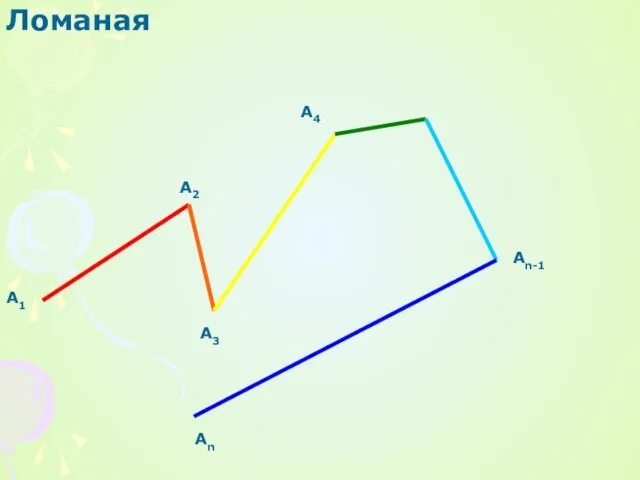 Презентация на тему Ломаная
Презентация на тему Ломаная  Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Математическая статистика
Математическая статистика Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника
Формула Эйлера для расстояния между центрами вписанной и описанной окружностей треугольника Презентация на тему Целое и части (1 класс)
Презентация на тему Целое и части (1 класс)  Построение сечений
Построение сечений Aproximarea numerică a funcţiilor. Metode numerice – curs 11
Aproximarea numerică a funcţiilor. Metode numerice – curs 11 Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА
Презентация на тему КОМПЛЕКСНЫЕ ЧИСЛА  Серединный перпендикуляр
Серединный перпендикуляр Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа)
Вычисление площадей фигур с помощью определенного интеграла. (Практическая работа) Сложение чисел
Сложение чисел Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Действия с векторами
Презентация на тему Действия с векторами  Площадь трапеции
Площадь трапеции Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Величины. Свойства величин
Величины. Свойства величин Функции. ЕГЭ
Функции. ЕГЭ Многочлены. Задания
Многочлены. Задания Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Понятие площади. Площадь квадрата и прямоугольника
Понятие площади. Площадь квадрата и прямоугольника Умножение. Законы умножения
Умножение. Законы умножения Презентация на тему Показательная и логарифмическая функции
Презентация на тему Показательная и логарифмическая функции  Комбинаторика. Из истории комбинаторики
Комбинаторика. Из истории комбинаторики Влияние коэффициентов квадратного трехчлена на расположение параболы
Влияние коэффициентов квадратного трехчлена на расположение параболы Пушкин и математика
Пушкин и математика